Magnetostatics

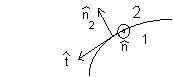
The fundamental equations magnetostatics are linear equations,
∇·B = 0,  ∇×B = μ₀j = j/(ε₀c²)  (SI units).
The principle of superposition holds.
The magnetostatic force on a particle with charge q is F = qv × B.

Definitions:

Drift velocity:  <v> = (1/N)∑_iv_i,   N = number of charge carriers.
Current density:  j = nq<v>,  n = N/V.
Current: I = dQ/dt = ∫_Aj·n dA.
The continuity equation is ∇·j = -∂ρ/∂t.  In statics ∂ρ/∂t = 0  -->  ∇·j = 0.

Currents and Circuits

Current:   I = ∫j·dA  or  I = dQ/dt.
Resistance:   R = ΔV/I.
Resistance of a straight wire:   R = ρl/A.
Power:   P = IΔV = I²R = (ΔV)²/R.
Resistors in series:   R = R₁ + R₂ + R₃ + ... .
Parallel Resistors:   1/R = (1/R₁) + (1/R₂) + (1/R₃) + ... .

Kirchhoff's first rule :  (Junction rule)
At any junction point in a circuit where the current can divide, the sum of the currents into the junction must equal the sum of the currents out of the junction.  (This is a consequence of charge conservation.)

Kirchhoff's second rule :  (Loop rule)
When any closed circuit loop is traversed, the algebraic sum of the changes in the potential must equal zero.  (This is a consequence of conservation of energy.)

Ampere's law

∮_ΓB∙dr = μ₀I_{through Γ}.
In situations with enough symmetry, Ampere's law alone can be used to find the magnitude of B. 
 

The flux of B through any closed surface is zero.  ∫_{closed surface} B·dA = 0.

The Biot-Savart law

B(r) = (μ₀/(4π))∫ dV' j(r')×(r-r')/|r-r'|³.
For filamentary currents we have  B(r) = (μ₀/(4π))∫ I dl'×(r-r')/|r-r'|³.

The magnetic vector potential

∇·B = 0 --> B = ∇×A.
A is not unique.  A' = A + ∇ψ + C, with ψ an arbitrary scalar field and C an arbitrary constant vector is also a vector potential for the same field.
In magnetostatics we choose ∇·A = 0. 
Then  ∇²A = -μ₀j,  A(r) = (μ₀/(4π)) ∫_V'dV' j(r')/|r - r'|.

The uniqueness theorem:

If the current density j is specified throughout a volume V and A or its normal derivatives are specified at the boundaries of a volume V, then a unique solution exists for A inside V.
Or, if the current density j is specified throughout a volume V and either A or B are specified at the boundaries of a volume V, then a unique solution exists for B inside V.

Boundary conditions in magnetostatics

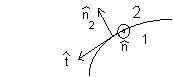
(B₂ - B₁)·n₂ = 0,  (B₂ - B₁)·t = μ₀k·n.
A is continuous across the boundary.

The force on a current distribution

F =  ∫_V j(r) × B(r) dV.
For filamentary currents we have F =  ∫_L I dl × B(r).

The magnetic dipole moment of a current distribution

m = IAn = ½∫_V r×j(r) dV.
The vector potential of a magnetic dipole at the origin is  A(r) = (μ₀/4π)m×r/r³. 
The magnetic field of a magnetic dipole at the origin is  B(r) = (μ₀/4π)(3(m·r)r/r⁵ - m/r³). 

The energy of a magnetic dipole in an external magnetic field is  U_mech = -m·B.
This is the mechanical work done to bring the dipole from infinity to its present position.

The force on a dipole is  F = ∇(m∙B).
The torque on a dipole is  τ = m × B.

Magnetic Materials

The magnetization M = dm/dV is defined as the magnetic dipole moment per unit volume. 

The total current density is due to free and to magnetization current densities.
j = j_f + j_m,  k_m = k_f + k_m,
j_m = ∇×M,  k_m = M×n.
H = B/μ₀ - M.  (This definition is not unique.)
∇×H = j_f,  (Ampere's law for H).

For linear, isotropic, homogeneous (lih) magnetic materials we have
M = Χ_mH,  B = μ₀(H + M) = μ₀(1 + Χ_m)H =  μ₀κ_mH =  μH.
Χ_m < 0 for diamagnetic materials, Χ_m > 0 for paramagnetic materials, permanent magnets are not lih.

Boundary conditions for H

(H₂ - H₁)·t₂ = k_f·n,  ∇·H ≠ 0  in general.

Energy in magnetostatics

The magnetostatic energy stored in a current distribution is given by 
U = (2μ₀)^-1∫_{all space}B·B dV.

In the presence of a magnetic material, the total work done in establishing a free current distribution is
W = ½∫_{all space}B·H dV,
or, in the presence of a lih magnetic material
U = (2μ)^-1∫_{all space}B·B dV.