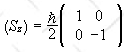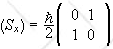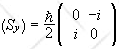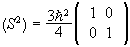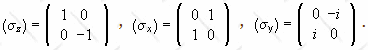Angular momentum

The operator J, whose Cartesian components satisfy the commutation relations
[J_i,J_j] = ε_ijkiħJ_k  
is defined as an angular momentum operator.  
For such an operator we have [J_i,J²] = 0, i.e. the operator J² = J_x² + J_y² + J_z² commutes with each Cartesian component of J.  We can therefore find an orthonormal basis of eigenfunctions common to J² and J_z.  We denote this basis by {|k,j,m>}.  
We have J²|k,j,m> = j(j + 1)ħ²|k,j,m>,  J_z|k,j,m> = mħ|k,j,m>.  
The index j can take on only integral and half integral positive values.  For a given j the index m can take on one of 2j + 1 possible values,  m = -j, -j + 1, ... , j - 1, j.  

We define the ladder operators J₊ = J_x + iJ_y and J_- = J_x - iJ_y.  
We then have J_x = ½(J₊ + J_-) and J_y = (-i/2)(J₊ - J_-) .
The operators J_± operating on the basis states {|k,j,m>} yield 
J_±|k,j,m> = [j(j+1) - m(m±1)]^½ħ|k,j,m±1>.

Orbital angular momentum

The operator L = R × P  satisfies the commutation relations [L_i,L_j] = ε_ijkħL_k and is called the orbital angular momentum operator.  We denote the  common eigenstates of L² and L_z by {|k,l,m>}.  In coordinate representation we have
L_z = (ħ/i)∂/∂φ
and
L² = -ħ²[(1/sinθ)∂(sinθ ∂/∂θ)/∂θ + (1/sin²θ)∂²/∂φ²].
The normalized common eigenfunctions of L² and L_z are called the spherical harmonics.

Properties of the spherical harmonics
Y_lm(θ,φ) = [(-1)^l/(2^l l!)][(2l+1) (l+m)!/(4π (l-m)!)]^½e^imφ(sinθ)^-md^l-m(sinθ)^2l/d(cosθ)^l-m.
We have
Y₀₀ = (4π)^-½,  Y_1±1 = ∓(3/8π)^½sinθ exp(±iφ),  Y₁₀ = (3/4π)^½cosθ,
Y_2±2 = (15/32π)^½sin²θ exp(±i2φ),  Y_2±1 = ∓(15/8π)^½sinθ cosθ exp(±iφ),
Y₂₀ = (5/16π)^½(3cos²θ - 1).

The Y_lm(θ,φ) form a complete set of functions of angle on the unit sphere.  Orthonormality is expressed through
∫₀^πsinθ dθ∫₀^2πdφ Y^*_l'm'(θ,φ)Y_lm(θ,φ) = δ_l'lδ_m'm.
and completeness is expressed through
∑_l=0^∞∑_m=-l^l Y^*_lm(θ,φ)Y_lm(θ',φ') = δ(cosθ - cosθ')δ(φ - φ') = δ(θ - θ')δ(φ - φ')/sinθ.

Complex conjugation
Y^*_lm(θ,φ) = (-1)^mY_l(-m)(θ,φ).

Parity
PY_lm(θ,φ) = Y_lm(π - θ,π + φ) = (-1)^lY_lm(θ,φ).
The parity of the spherical harmonics is well defined and depends only on l.

Addition of angular momentum

Consider two angular momentum operators J₁ and J₂.  
J₁ operates in E₁ and J₂ operates in E₂. 
Let J = J₁ + J₂.  J operates in E = E₁⊗ E₂.  Since the operators J₁², J_1z , J₂², and J_2z all commute, a basis of common eigenvectors for E exists.  We denote this basis by {|j₁,j₂;m₁,m₂>}.  Since the operators J₁², J₂², J², and J_z all commute, a basis of common eigenvectors for E exists.  We denote this basis by {|j₁,j₂;j,m>}.  We can write the vectors of one basis as linear combinations of the vectors of the other basis.
|j₁,j₂;j,m> = ∑_m1∑_m2 C^j_m1m2|j₁,j₂;m₁,m₂>,
|j₁,j₂;m₁,m₂> = ∑_j∑_m C^j_m1m2|j₁,j₂;j,m>.
The C^j_m1m2 = <j₁,j₂;m₁,m₂|j₁,j₂;j,m> are called the Clebsch-Gordon coefficients.

Properties of the Clebsch-Gordan coefficients
C^j_m1m2 = real, C^j_m1m2 = 0 unless m₁ + m₂ = m and |j₁ - j₂| ≤ j ≤ |j₁ + j₂|.
C^j_{m1=j1 m2=j2} = 1  (stretched case).

Spin ½

The state space of a spin ½ particle is two-dimensional.
The common orthonormal eigenbasis of S² and S_z is {|+>, |->}.
Below are matrices of spin operators in this basis.

        

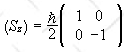
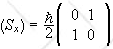
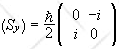
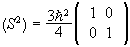
We write S = (ħ/2)σ.  The matrices



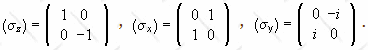
are the Pauli matrices.

Properties of σ_x and σ_y and σ_z
det(σ_i) = -1,  Tr{σ_i} = 0,  σ_i² = I,  σ_xσ_y = -σ_yσ_x = iσ_z.
In general, σ_iσ_j =  iε_ijkσ_k + δ_ijI,   [σ_i,σ_j] = i2ε_ijkσ_k.
Therefore 
[S_x,S_y] = iħS_z,   [S_y,S_z] = iħS_x,    [S_z,S_x] = iħS_y,
since S = (ħ/2)σ.

The operator S_u is defined through S∙u = S_xsinθcosφ + S_ysinθsinφ + S_zcosθ.
The matrix of S_u is (S_u) = (S_x)sinθcosφ + (S_y)sinθsinφ + (S_z)cosθ.

The eigenvectors of S_u are
|+>_u = cos(θ/2)exp(-iφ/2)|+> + sin(θ/2)exp(iφ/2)|->,
|->_u = -sin(θ/2)exp(-iφ/2)|+> + cos(θ/2)exp(iφ/2)|->.
Therefore |+> = cos(θ/2)|+>_u - sin(θ/2)|->_u,  |-> = sin(θ/2)|+>_u + cos(θ/2)|->_u. 

A system of two spin ½ particles

Let E_s = E_s(1)⊗E_s(2) be the state space of a system of two spin ½ particles.
The tensor product vectors {|++>, |+->, |-+>, |-->} form a basis for E_s.
In the four dimensional state space the operators S_iz are product operators.
S_1z = S_1z(1) ⊗ I(2), S_2z = I(1) ⊗ S_2z(2), etc. 
The common eigenvectors of S² = (S₁ + S₂)² and S_z = S_1z + S_2z also form a basis of E_s, which we denote by {|S,S_z>}, where s(s + 1)ħ² denotes the eigenvalue of S² and m_sħ denotes the eigenvalue of S_z.
We have the singlet state
|00> = 2^-½(|+-> - |-+>)
and the triplet states
|11> = |++>,
|10> = 2^-½(|+-> + |-+>),
|1-1> =|-->.