 AC and DC circuits
AC and DC circuitsAny two-terminal network of passive elements is equivalent to an effective impedance Zeff.
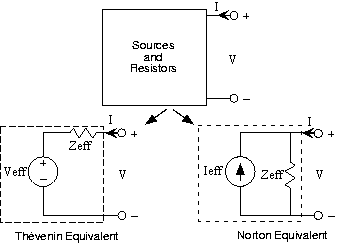
Thevenin equivalent circuits: Any two terminal network can be replaced by a generator εeff in series with an impedance Zeff.
Passive circuit elements:
Resistor: V = IR
Capacitor: V = Q/C
Inductor: V = LdI/dt
Kirchhoff's rules for filamentary circuits:
For each loop
∑n Vn = 0, for each
node
∑n In = 0.
Assume V(t), I(t), ε(t) are all proportional to exp(iωt).
Assume idealized circuit elements. Define the impedance Z = V/I.
Then
Z(capacitance) = ZC = 1/(iωC),
Z(inductance) = iωL,
Z(resistance) = ZR = R.
Any impedance may be written as Z = R + iX.
Power:
Pavg = ½Re(VI*) = I2rmsR. The maximum power is delivered to a load when Zload = Zeff*.
(See below, equivalent circuits.)
 AC and DC circuits
AC and DC circuits
Any two-terminal network of passive elements is equivalent to an effective
impedance Zeff.
Thevenin equivalent circuits: Any two terminal network can be replaced by
a generator εeff in series with an
impedance Zeff.
Norton equivalent circuits: Any two terminal network can be replaced by a current source Ieff in parallel with an impedance Zeff.
 Ladder networks:
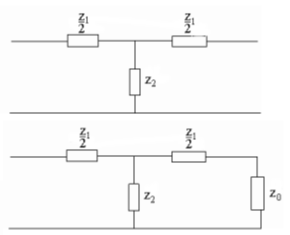
Ladder networks:Consider an infinite ladder network of reactive elements, for example the network
shown on.
The network has some impedance Z0. Adding another element to
the front of the infinite ladder network does not change Z0. The network
with impedance Z0 is therefore equivalent to the network shown below, terminated by Z0.
We can calculate Z0. For the example
shown, Z0 = (Z12/4
+ Z1Z2)½.
Z0 = R + iX.
If the ladder contains no resistors, then Z0 is either real or
imaginary. If Z0 is real, the circuit absorbs energy, if Z0
is imaginary, it does not absorb energy. If Z0 is real
signals can pass to the load, if Z0 is imaginary, signals
cannot pass to the load, we have a filter.