Elastic scattering

In a typical scattering experiment a target is struck by a beam of mono-energetic particles.
Let F_i be the incident flux, i.e. the number of particles per unit area per unit time. 
F_i = n_pv, where n_p is the number of particles per unit volume. 
Typically n_p is very small and we can neglect any interaction between different incident particles.
We measure the number ΔN_p of particles scattered per unit time into a solid angle ΔΩ about the direction defined by the spherical coordinates θ and φ. 
We expect ΔN_p ∝ F_i, and ΔN_p ∝ ΔΩ .
We define ΔN_p = σ_t(θ,φ)F_iΔΩ.  Here σ_t(θ,φ) is the differential scattering cross section of the target.  It has the units of an area.  Commonly used units are cm² and barn = 10^-24 cm².

The partial wave method

Assume a central potential energy function of finite range, i.e. U(r) --> 0 as r --> ∞ faster than 1/r.
Then stationary state solutions of the eigenvalue equation  HΦ_k(r) = E_kΦ_k(r) with the asymptotic form
Φ_k(r) = e^ikz + f_k(θ) e^ikr/r = ∑_l=0^∞ c_l P_l(cosθ) sin(kr - lп/2 + δ_l)/(kr)
exist.  Here
f_k(θ) = (1/k)∑_l=0^∞(2l+1)exp(iδ_l)sinδ_lP_l(cosθ)
is the scattering amplitude, δ_l is called the phase shift of the lth partial wave.
The differential scattering cross section is
σ_k(θ) = dσ_k/dΩ = |f_k(θ)|² = (1/k²)|∑_l=0^∞(2l+1)exp(iδ_l)sinδ_lP_l(cosθ)|²,
and the total scattering cross section is
σ_k = ∫∫σ_k(θ)sinθdθdφ = (4п/k²)∑_l=0^∞(2l+1)sin²δ_l.
Let R be the range of the potential.  If kR << (l(l + 1))^½, then δ_l = 0.

Low energy scattering

Assume kR << (l(l + 1))^½ for all l except l = 0.  Then
f_k(θ) = (1/k)exp(iδ₀)sinδ₀,  σ_k(θ) = (1/k²)sin²δ₀,  and  σ_k = (4п/k²)sin²δ₀. 
This is called s-wave scattering.

[To derive the expression f_k(θ) = (1/k)∑_l=0^∞(2l+1)exp(iδ_l)sinδ_lP_l(cosθ) we expand Φ_k(r) in terms of the common eigenfunctions of H, L² and L_z, |klm> = (u(r)/r)Y_lm(θ,φ).  In classical mechanics, a free particle with angular momentum L about the origin and momentum p moves in a straight line with closest distance to the origin b = L/p;  b is called the impact parameter relative to the origin. 
If L = ħ(l(l + 1))^½ and p = ħk, then b_l(k) = (1/k)(l(l + 1))^½.
b_l(k) is the radius where the angular momentum barrier potential, U_eff(r) = l(l+1)ħ²/(2mr²) is equal to the total energy of the free particle.
l(l+1)ħ²/(2m(b_l(k))²) = ħ²k²/(2m),  b_l(k) = (1/k)(l(l + 1))^½.
In Quantum Mechanics, for r < b_l(k), in the classically forbidden region, the eigenfunctions |klm> can only have an approximately exponentially decaying tail.
In a finite range potential, if the partial wave with angular momentum quantum number l only has an approximately exponentially decaying tail in the region where the potential is non-zero, then it is minimally affected by the potential and the phase shift δ_l is approximately zero.]

For a finite range potential U(r) of range R the phase shift δ₀ is negative if  U(r)_r<R > 0, and it is positive if  U(r)_r<R < 0.  If  U(r)_r<R = ∞ then δ₀ = kR, σ_k = 4пR², if kR << 1.
For  U(r)_r<R < 0 we can have δ₀ = п/2 while kR << 1, then σ_k = 4п/k² --> ∞ as E --> 0.  If  δ₀ = п, then σ_k = 0.  This is called the Ramsauer-Townsend effect.

The Born approximation

The elastic scattering cross section in the Born Approximation is
σ_k^B(θ,φ) = σ_k^B(k,k') = [μ²/(4п²ħ⁴)]|∫d³r' exp(-iq∙r')U(r')|²,
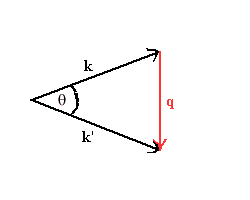
where q = k' - k, k = μv₀/ħ, k' = μv₀/ħ (k'/k'), and μ is the reduced mass.

The differential scattering cross section is proportional to the square of the Fourier transform of the potential.
We often want to know the scattering cross section as a function of the scattering angle and not as a function of the momentum transfer.  Let θ be the angle between k and k'.  Then q = 2ksin(θ/2).