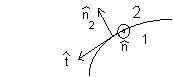Electromagnetic waves

Review Maxwell's equations!
In lih materials in regions with ρ_f = 0 and j_f = 0 both E and B satisfy the wave equation.
∇²E - με∂²E/∂t² = 0,  ∇²B - με∂²B/∂t² = 0.
Plane wave solutions E = E((k/k)∙r) - vt,  B = B(k/k)∙r - vt) exist. 
Here  k/k is the unit vector pointing in the direction of propagation.
We have  E ⊥ B,  E ⊥ k,  B ⊥ k,  B = (με)^½(k/k)×E.
Sinusoidal plane waves are of the form  E = E₀e^{i(k∙r - ωt)}.  B = B₀e^{i(k∙r - ωt)},
with k² = μεω².

In regions with ρ_f = 0 and j_f = σ_cE both E and B satisfy the damped wave equation.
∇²E - μσ_c∂E/∂t - με∂²E/∂t² = 0,  ∇²B - μσ_c∂B/∂t - με∂²B/∂t² = 0.
Plane wave solutions exist.   For sinusoidal plane waves we now have
k² = iμσ_cω + μεω² = με(ω)ω², i.e.  k is complex, the wave damps out.
ε(ω) and the index of refraction are complex numbers.

The skin depth is defined as the distance it takes to reduce the amplitude by a factor of 1/e.

Plane waves at dielectric-dielectric boundaries

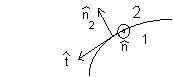(D₂ - D₁)·n₂ = σ_f,
(B₂ - B₁)·n₂ = 0,
(E₂ - E₁)·t = 0,
(H₂ - H₁)·t = k_f∙n.

These are the boundary conditions the electromagnetic fields have to satisfy on any boundary. 
For waves propagating across a dielectric-dielectric boundary or from a dielectric into a conductor we use that the tangential components of E and H are continuous across the boundary. 
From these boundary conditions we derive the law or reflection, θ_i = θ_r, and the law of refraction, (Snell's law), n₁sinθ_i = n₂sinθ_t, for a wave propagating from a medium with index of refraction n₁ into a medium with index of refraction n₂.  Here θ_i, θ_r, and θ_t are the angles the incident, reflected, and transmitted wave vectors make with the normal to the boundary.
The plane of incidence is the plane containing the wave vector k_i and the normal to the boundary. 
A linear polarized wave has p-polarization if E lies in the plane of incidence, and it has s-polarization if E is perpendicular to the plane of incidence.
The reflection coefficients for s and p polarization are
r_12s = sin(θ₁ - θ₂)/sin(θ₁ + θ₂),   r_12p = tan(θ₁ - θ₂)/tan(θ₁ + θ₂). 
The reflectance is  R = |r₁₂|².  The transmittance is T = 1 - R if there is no absorption (energy conservation).

Polarization by reflection

When θ_i = θ_B, the Brewster angle, then only light with s-polarization is reflected. 
We have tan θ_B = n₂/n₁,  θ_t + θ_i = π/2.

Total internal reflection

If n₂ < n₁, then for  θ_i > θ_c = sin^-1(n₂/n₁)  we have total internal reflection.  The wave vector k_t then has a component parallel to the interface which is real and a component perpendicular to the interface which is imaginary.

Reflection by a good conductor

For good conductors R ≈ 1, T ≈ 0.  The wave does not penetrate into the conductor.  We then use as the boundary conditions that the tangential component of E and the normal component of B are continuous.

Waveguides

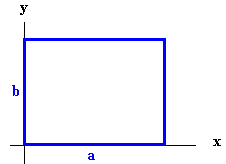Electromagnetic waves can propagate in a conducting channel.
If we have a rectangular channel as shown in the figure, with its axis in the z-direction, than any wave propagating into the z-direction can be viewed as a superposition of waves with either the electric or the magnetic field vector lying in the x-y plane.  These waves are called transverse electric (TE) or transverse magnetic (TM) waves.
E and B have to satisfy boundary conditions on the conducting walls of the channel.
E∙t = 0 and B∙n = 0 on the walls.
A TE wave is a superposition of waves of the form 
E = E_0ysink_xx exp(i(k_zz - ωt)) j + E_0xsink_yy exp(i(k_zz - ωt)) i,
with  k_xa = nπ,  k_yb = mπ, with m and n positive integers.  One of these integers, n or m, may be zero. 
These waves are called the TE_mn modes of the waveguide. 
For each mode there exists a cutoff frequency ω_c = ((nπc/a)² + (mπc/b)²)^½. 
Waves with ω < ω_c do not propagate in the waveguide. 
If a > b then the cutoff frequency for all TE modes is ω_c = nπc/a.

Phase velocity:  The phase velocity v_p is the velocity with which planes of constant phase move in the z-direction.
v_p = ω/k_z > c. 
Group velocity:  The group velocity v_g is the velocity with which the energy moves in the z-direction.
We have v_g < c,  v_pv_g = c².

A TM wave is a superposition of waves of the form 
B = B_0xsink_xx exp(i(k_zz - ωt)) j + B_0ysink_yy exp(i(k_zz- - ωt)) i,
with  k_xa = nπ,  k_yb = mπ, with m and n nonzero, positive integers. 
These waves is called the TM_mn modes of the waveguide. 
TM₁₀ or TM₀₁ guided waves do not exist.  They cannot satisfy ∇∙B = 0.

Electromagnetic waves formulas