
Consider a particle moving in a central potential.
U = U(r), F = f(r)(r/r), f(r) = -dU/dr.
In
a central potential the energy E and the angular momentum M
are conserved. The motion is in a plane.
Choose this plane to be the x-y plane. Then
L = T - U = ½m[(dr/dt)2 + r2(dφ/dt)2]
- U(r).
E = T + U = ½m[(dr/dt)2 + r2(dφ/dt)2]
+ U(r) = constant.
M = pφ =
∂L/∂(dφ/dt) = mr2(dφ/dt) = constant, angular momentum is
conserved.
Areal velocity = dA/dt =
½r(rdφ/dt) = ½r2(dφ/dt) =
constant.
The area swept out per unit time is constant for all central potentials.
E = ½m(dr/dt)2 + M2/(2mr2)
+ U(r) = ½m(dr/dt)2 + Ueff(r),
with
Ueff(r) = M2/(2mr2)
+ U(r).
yields dr/dt = ±[(2/m)(E - Ueff(r))]½.
Lagrange's equations yield
md2r/dt2 - M2/(mr3) = f(r),
or
md2r/dt2 = -dUeff/dr,
with f(r) = -dU/dr.
dφ = [M/(mr2)]dt, d/dt = [M/(mr2)] d/dφ.
From
dr/dt = [(2/m)(E - Ueff(r))]½
we obtain
dφ = [M/(mr2)]dr [(2/m)(E - Ueff(r))]-½.
φ = ∫M(dr/r2)/[2m(E - Ueff(r))]½
+ φ0,
or, with u = 1/r,
φ = φ0 - ∫Mdu/[2m(E - Ueff(u))]½.
From
md2r/dt2 - M2/(mr3) = f(r)
we obtain
(M/r2) d/dφ[(M/(mr2))dr/dφ] - M2/(mr3) = f(r),
or
(M2u2/m)(d2u/dφ2
+ u) = -f(u), where u = 1/r.
Let U(r) = -α/r,
Ueff(r) = -α/r
+ M2/(2mr2), f(r) = -α/r2.
Then the equation for the orbit yields
φ = cos-1[(M/r - mα/M)/(2mE +
m2α2/M2)½]
+ φ0.
cos(φ - φ0)
= (1/e)(p/r - 1),
with p = M2/(mα),
e = (1 + 2EM2/(mα2))½,
or
p/r = 1 + e cos(φ -
φ0).
This is the equation of a conic section.
Here e is the eccentricity.
| E > 0, e > 1 | hyperbola | |||
| E = 0, e = 1 | parabola | |||
| E < 0, e < 1 | ellipse | |||
| E = -mα2/(2M2), e = 0 | circle |

The ellipse and the circle are closed orbits.
For closed orbits we have
rmin = p/(1 + e), rmax = p/(1 - e),
semi-major axis: a = ½(rmin +
rmax) = p/(1 - e2) = ½α/|E|,
semi-minor axis: b = a(1 - e2)½ = M/(2m|E|)½.
From
dA/dt = M/(2m), A = MT/(2m) = πab
we find the period T.
T = 2mπab/M = 2π(m/α)½a3/2.
This is Kepler's third law. It only
holds for the attractive 1/r potential.
For the gravitational potential V(r) = -GM/r remember:
All orbits with the same semi-major axis have the same total energy per unit
mass and the same period.
Consider two particles with masses m1 and m2, subject to
internal forces
F12 = F12(r2
- r1)/r12, r12 = |r1 -
r2|,
F21 = -F12.
The
equations of motion are
m1(dv1/dt) =
F21,
m2(dv2/dt) =
F12 = -F21, m1dv1/dt
+ m2dv2/dt = 0.
Define the center of mass (CM)
coordinate R = (m1r1
+ m2r2)/(m1+ m2).
The center of mass moves with constant velocity.
Define the relative
coordinate r = r1 -
r2.
Then r1
= R + (m2/(m1+m2))r,
r2 = R - (m1/(m1 + m2))r
.
We find that (m1m2/(m1+ m2 ))d2r/dt2
= F21(r), or μd2r/dt2
= F21(r).
Here μ
= m1m2/(m1
+ m2) is called the reduced mass.
The problem of the relative motion of
two interacting masses m1 and m2 can be solved by
solving for the motion of one fictitious particle of reduced mass μ
in a central field.
Equation of motion of
the fictitious particle:
μd2r/dt2 =
F21(r) = F21(r)(r/|r|).
The equations of the motion for the system can be separated into equations for the center of mass motion and equations for the relative motion. Similarly, the sum of the momenta and sum of the angular momenta can be split into parts pertaining to the center of mass motion and parts pertaining to the relative motion.
In the CM frame of two interacting particles the Lagrangian
L = ½m1(dr1/dt)2
+ ½m2(dr2/dt)2 - U(|r1
- r2|)
can be written as
L = ½μ(dr/dt)2 - U(r),
μ = m1m2/(m1 + m2),
r = r1 -
r2.
The problem of two interacting particles in their CM frame is equivalent to
the problem of a fictitious particle of
reduced
mass μ moving in a
central potential U(r).
Consider the scattering of a particle by a central
potential.
We define the differential scattering cross section
σ(Ω) = dσ/dΩ through the expression
# of particles scattered into the solid angle dΩ per unit time = I σ(Ω) dΩ ,
where I
is the intensity of the incident beam, i.e. the number of beam
particles per unit area per unit time.
For a central potential σ(Ω) is independent of
φ.
We write
σ(Ω) = σ(θ)
= dσ/dΩ.
The number of particles scattered through an angle between
θ and
θ
+ dθ
per unit time is
I σ(θ) 2π sinθ
dθ.
We define the impact parameter b
through
M = mv0b = b(2mE)½,
where M is the angular momentum and v0 is the incident speed at
infinite distance.
Once E and b are fixed, the scattering angle is uniquely
determined.
A particle incident with impact parameter between b and b + db will be scattered
through an angle between
θ and
θ + dθ. We can write
I 2π σ(θ) sinθ dθ
= -I 2π b db,
σ(θ)
=|(b/sinθ)(db/dθ)|.
In a central potential the motion is in a plane and M and E are constant.
E = ½m(dr/dt)2 + M2/(2mr2) + U(r) = ½m(dr/dt)2 + b2E/r2 + U(r), since M = mv0b =
b(2mE)½.
dr/dt = ±[(2/m)(E(1 - b2/r2) - U(r))]½.
M = mr2(dφ/dt), d/dt = [M/(mr2)]d/dφ = [b(2mE)½/(mr2)]d/dφ.
From dr/dt = [(2/m)(E(1 - b2/r2) - U(r))]½
we then find the equation for the trajectory.
dr/dφ = [(2/m)(E(1 - b2/r2) - U(r))]½/ [b(2mE)½/(mr2)]
= [(E½ (1 - b2/r2) - U(r))]½/ (b/r2).
dφ/dr = (b/r2)/ [(E½ (1 - b2/r2) - U(r))]½.
dφ/du = -b/ [(E½ (1 - b2u2) - U(u))]½, with u = 1/r.
φ(u) = b∫0udu'/[1 - b2u'2 - U(u')/E]½, with φ(z = -∞) = 0.
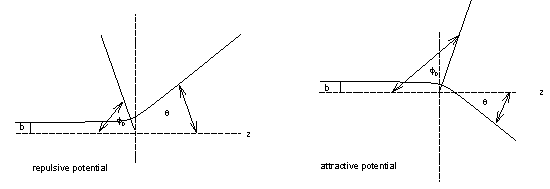
Let θ be
the angle between the incident and the scattered direction and φ0 be the angle between
r(z =
-∞)
and rmin.
Then
φ0 = b∫0umaxdu'/[1
- b2u'2 - U(u')/E]½,
and
E =
M2/(2mr2min)
+ U(rmin) = b2E/r2min
+ U(rmin) = b2Eu2max
+ U(umax)
determines umax. We have
θ
= π - 2φ0
for a repulsive potential,
θ
= 2φ0 - π
for an attractive potential, (or θ = π - 2φ0, θ
< 0.
If U(r) = α/r, U(u) = αu, U(umax) = αumax, then
umax = -α/(2b2E) + [α2/(4b4E2)
+ 1/b2]½ and φ0
= cot-1(α/(2bE)).
cotφ0
= α/(2bE), cot(θ/2) = cot(π/2 - φ0) = tanφ0
= 1/cotφ0.
b = [α/(2E)]cot(θ/2), db/dθ = -½[α/(2E)]sin-2(θ/2),
σ(θ) = ¼[α/(2E)]2/sin4(θ/2).
This is the Rutherford's formula.
Let θ be the scattering angle in the lab frame and θ0 be the
scattering angle in the CM frame. The number of particles scattered into a detector is the same in the
laboratory and in the CM frame. Therefore
σ(θ) sinθ dθ
=
σ(θ0)
sinθ0 dθ0.