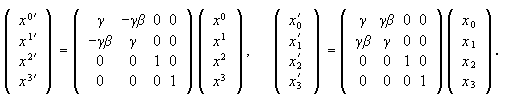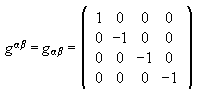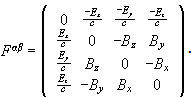Relativistic E&M

Electrodynamics in relativistic notation

A contravariant 4-vector is a set of 4 quantities which transform under a Lorentz transformation like (ct,r) = (x⁰,x¹,x²,x³). 
(A⁰,A¹,A²,A³) is a contravariant 4-vector if A'^α = (∂x'^α/∂x^β)A^β.  The repeated index β is summed over.

A covariant 4-vector is a set of 4 quantities which transform under a Lorentz transformation like (ct,-r) = (x₀,x₁,x₂,x₃). 
(A₀,A₁,A₂,A₃) is a covariant 4-vector if A'_α = (∂x^β/∂x'^α)A_β.
If the primed coordinate system moves with velocity v = βci with respect to the unprimed one, then



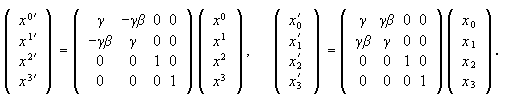
β = v/c,   β = v/c,  γ = (1 - β²)^-½.

A contravariant tensor of second rank is a set of 16 quantities which transform under a Lorentz transformation according to F'^αβ = (∂x'^α/∂x^γ)(∂x'^β/∂x^δ)F^γδ.
A covariant tensor of second rank transforms under a Lorentz transformation according to G'_αβ = (∂x^γ/∂x'^α)(∂x^δ/∂x'^β)G_γδ,
and a mixed tensor transforms according to H'^α_β = (∂x'^α/∂x^γ)(∂x^δ/∂x'^β)H^γ_δ.

Special tensors:
δ^α_β = (∂x^α/∂x^β) is the Kroneker delta extended to 4 indices.

 
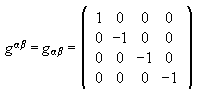
is the metric tensor.
The dot product between two contravariant 4-vectors is defined as A∙B = g_αβA^αB^β = A_βB^β = A^αB_α.  It is invariant under a Lorentz transformation, it is a Lorentz scalar.

Important 4-vectors:

x^μ = (ct,r), 
u^μ = (γc,γv) = 4-vector velocity,
p^μ = (γmc,γmv) = (E/c,p) = (p₀,p) = 4-vector momentum,
(∂/∂x_μ) = ∂^μ = (∂/∂x₀,-∇) = 4-dimensional gradient,
j^μ = (cρ,j) = 4-vector current,
A^μ = (Φ/c,A) = 4-vector potential.

The divergence of a 4-vector ∂_μA^μ = ∂A⁰/∂x⁰ + ∇∙A  is a Lorentz scalar.

Examples:
∂^μ∂_μ = ∂_μ∂^μ = (1/c²)∂²/∂t²  - ∇²  is the D'Alambertian.  It is invariant under a Lorentz transformation.

(∂^μ∂_μ)A^μ = j^μ/(ε₀c²)
is the inhomogeneous wave equation for the potentials.  It holds in every inertial frame.

∂^μj_μ = ∂_μj^μ = ∂ρ/∂t + ∇∙j  is invariant under a Lorentz transformation.
∂ρ/∂t + ∇∙j = 0 is the statement of charge conservation.
If charge is conserved in one inertial frame, it is conserved in every inertial frame.

∂^μA_μ = ∂_μA^μ = (1/c²)∂Φ/∂t - ∇∙A is invariant under a Lorentz transformation.
∂^μA_μ = ∂_μA^μ = (1/c²)∂Φ/∂t - ∇∙A = 0 is the Lorentz condition.  If the Lorentz condition holds in one inertial frame, it holds on every inertial frame.

Transformation of the fields

All contravariant 4-vectors A^μ transform as A'⁰ = γ(A⁰ - β∙A), A'_||= γ(A_|| - βA⁰), A'_⊥ = A_⊥.
The antisymmetric field strength tensor is defined through F^αβ = ∂^αA^β - ∂^βA^α.  It is a second rank contravariant tensor.


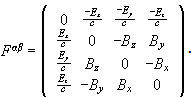
The transformation F'^αβ = (∂x'^α/∂x^γ)(∂x'^β/∂x^δ)F^γδ yields
E'_|| = E_||,  B'_|| = B_||,
E'_⊥ = γ(E + v×B)_⊥,
B'_⊥ = γ(B - (v/c²)×E)_⊥.
Here || and ⊥ refer to the direction of the relative velocity.

Invariants

E² - c²B² and (E∙B)² are invariant under a Lorentz transformation.