Space-time diagrams

Space-time diagrams refer to an inertial frame.  Let us consider two inertial frames, A (Alice) and B (Bob).  For simplicity, let us only consider one spatial dimension.  Assume Bob moves with constant velocity v with respect to Alice. 
Initially we are only concerned with how to draw a space-time diagram in Alice's reference frame.

Alice's rules for drawing space-time diagrams:

1. In a space-time diagram two or more events that have the same space-time coordinates are represented by the same point.
2. Events that have the same space coordinate, but not the same time coordinates are represented by points on a single straight line, a line of constant position.  Alice is free to orient one such line of constant position anyway she chooses.

   
   Line of constant position
   The two red dots represent two events with the same space but different time coordinates.
    

3. Any two lines of constant position representing events with different space coordinates must be parallel.  If they were not parallel they would intersect somewhere, and their point of intersection would correspond to a single event with two different space coordinates.  An event, however, is characterized by unique space and time coordinates.
4. The distance on the page between two distinct lines of constant position is proportional to the actual distance between the positions of the events they represent.  The quantitative relation between distances in space and distances in the diagram is given by a scale factor λ.

   
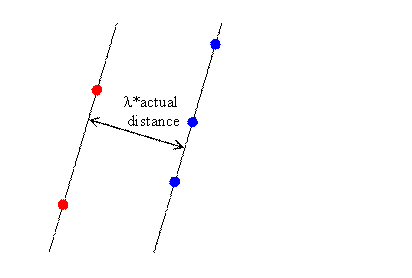
   Two lines of constant position
   The red dots represent events with the same space coordinate and different time coordinates.
   The blue dots also represent events with the same space coordinate and different time coordinates,
   but the space coordinate of the blue dots is different from the space coordinate of the red dots.
    

5. Events that have the same time coordinate, but not necessarily the same space coordinate are represented by points on a single straight line, a line of constant time.  Alice is free to orient one such line of constant time to make any angle she wishes with her lines of constant position, except 0^o.
6. Any two lines of constant time representing events with different space coordinates must be parallel.  If they were not parallel they would intersect somewhere, and their point of intersection would correspond to a single event with two different time coordinates.

   
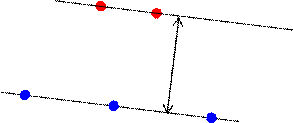
   Two lines of constant time
   The red dots represent events with the same time and different space coordinates. 
   The blue dots also represent events with the same time coordinate and different space coordinates,
   but the time coordinate of the blue dots is different from the time coordinate of the red dots.
    

7. The distance on the page between two distinct lines of constant time is proportional to the actual time interval between the times of the events they represent.
8. Any line of constant time intersects any line of constant position in precisely one point, which represents those events that have exactly these space-time coordinates.
9. It is convenient to calibrate the time axis in units of distance by using ct instead of t, and to use the same proportional constant λ for distance and c*time.
10.  The distance μ along any line of constant position associated with two events separated by one unit in space is exactly the same as the distance along any line of constant time associated with two events separated by one unit in time (ct).  Note that the scale factor μ is bigger than the scale factor λ unless Alice takes her lines of constant time perpendicular to her lines of constant position, in which case μ = λ.  In general λ = μ sin(2α), where 2α is the smallest angle between the lines of constant position and the lines of constant time.

    
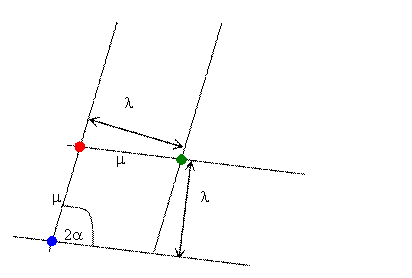
    The blue and the red point are two events with the same space coordinate, separated by one unit of ct. 
    The red and the green dot are two events with the same time coordinate separated by a distance of one unit.

A particularly important collection of events for an object is the set of all events at which the object is present.  The totality of all such events is represented by a continuous line in the space-time diagram.  This line, which represents the entire history of the object, is called the world line of the object.  An object which is stationary in Alice's frame of reference throughout its entire history is represented by the line of constant position.  An object moving with constant velocity in Alice's frame of reference is represented by a straight line that is not parallel to any line of constant position, since the object is at different positions at different times.
The world lines of objects moving with the same constant velocity are parallel lines.  An especially important world line is the space-time trajectory of a photon. 

11. The angle that lines of constant position make with the world line of a photon is the same as the angle that lines of constant time make with that trajectory.
12.  The trajectories of two photons moving in opposite directions are perpendicular to each other in the space-time diagram.

    
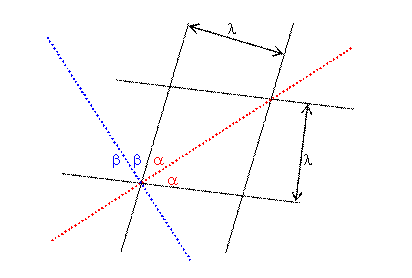
    The dotted lines represent the world lines of two photons traveling in opposite directions.
    For the angles we have α + β = 90^o.

13.  Alice can rotate her diagram so that the world lines of two photons moving in opposite directions are symmetric about the vertical direction, tilted 45^o degrees to the right and left, respectively.  Her lines of constant position will then tilt away from the vertical at the same angle that her lines of constant time tilt away from the horizontal.  With this convention for orienting the diagram, lines of constant time are always more vertical than horizontal, while lines of constant position are always more horizontal than vertical.

    
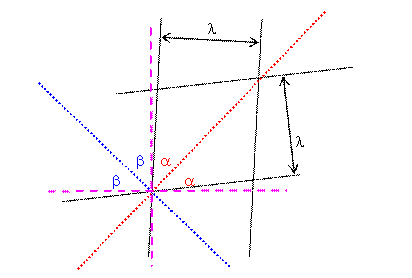
    Alice's space-time diagram

The above rules completely determine the structure and orientation of the system of lines of constant time and constant position that Alice uses to locate events in space and time except for two choices still available to her:
(a)  She is free to choose the scale factor λ.
(b)  She is free to choose the angle 2α that her lines of constant time make with her lines of constant position or, equivalently, the angle a that both families of lines make with the photon lines.  Her choices of λ and α fix μ. 

Her choice of α depends on how she wants to use her diagram.  If she is only using it to chart events in her own reference frame, then a symmetric choice is to take 2α to be 90^o, so that her lines of constant position are vertical and her lines of constant time are horizontal.  If, however, she wishes to compare her description of events with the description of the same events provided by an observer in another inertial frame of reference, then taking 2α to be 90^o may not be the best choice.

How can Bob use Alice's space-time diagram and convert it to a space time diagram drawn in his inertial frame?

Bob's frame of reference has velocity v with respect to Alice's frame.  Bob's lines of constant position are therefore parallel to the word line of an object that is moving with velocity v in Alice's frame.  Bob's lines of constant position are parallel straight lines that are not parallel to Alice's lines of constant position.  The faster Bob moves with respect to Alice, the more they tilt away from Alice's lines.  Lines of constant time and lines of constant position in Alice's diagram, drawn through any two points on one of Bob's lines of constant position, define a parallelogram.  The ratio of the lengths of the sides of this parallelogram is just the relative speed v of the two reference frames.

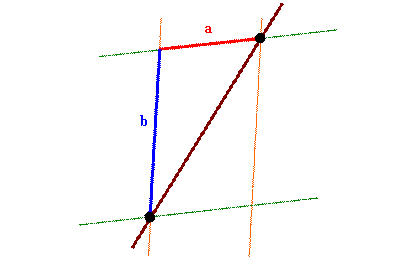
The brown line is a line of constant position in Bob's frame,
i.e. it is the world line of an object at rest in Bob's frame.
The orange lines are lines of constant position and the green lines are lines of constant time in Alice's frame. 
The velocity of Bob with respect to Alice is v/c = a/b. 
In Alice's frame the position of the object changes by an amount μa and the time by and amount μb/c.

What are Bob's lines of constant time?

Consider a set of events associated with a clock synchronization experiment, on a train that is stationary in Bob's frame of reference.  The left end, right end, and middle of this a train are represented in Alice's space-time diagram by parallel world lines of objects moving with constant velocity v.  The lines are equally spaced, since Alice and Bob agree on which point describes the middle of the train.  Two photons emitted together in the middle of the train travel in opposite directions with the same speed c.  The train is at rest in Bob's frame, and the photons arrive at the opposite ends of the train at the same time in Bob's reference frame.  In Alice's frame we draw a pair of 45^o lines starting at a point on the world line of the middle of the train.  These lines represent the trajectories of photons moving toward the front and rear.  The points of intersection of the two photons with the two ends of the train represent simultaneous events in Bob's frame and therefore lie on one of his lines of constant time.

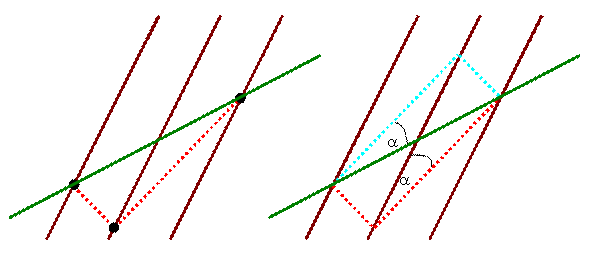
The diagram is drawn in Alice's frame. 
The brown lines are the world lines of three equally spaced objects which are stationary in Bob's frame. 
The low black dot represents the event of two photons being emitted in opposite directions from the middle object.  
The upper black dots represent the two events of the photons being detected by the other two objects. 
In Bob's frame of reference these are simultaneous events. 
The green line joining the upper two dots is a line of constant time in Bob's frame. 

Bob's lines of constant time in Alice's diagram must make the same angle with the photon trajectories as his lines of constant position.  In addition, the spacing of Bob' lines of constant c*time one unit apart is the same as the spacing of Bob's lines of constant position one unit of distance apart in Alice's diagram.

How to construct Bob's space-time diagram given Alice's diagram

Draw Alice's diagram.  Choose the orientation of the ct and x axes.  Draw the world line of an object moving with velocity v in Alice's frame.  That world line makes an angle θ with Alice's ct axis.  It is Bob's ct' axis.  Bob's x' axis makes an angle -θ with Alice's x axis.

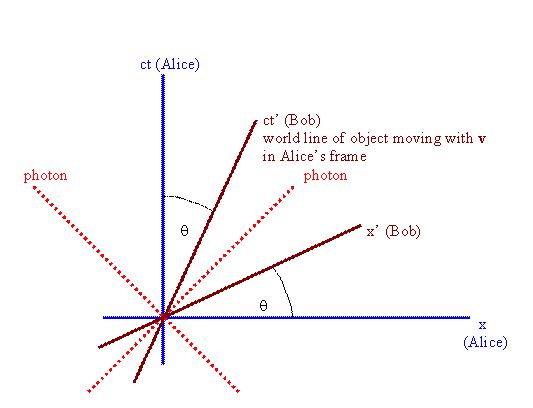
The rules for the orientation of Alice's lines of constant time and constant position and the relationship between their scales impose restrictions on the lines of constant position and time that Bob must use, if he wishes to represent events with the same points that Alice uses in her diagram.  Those restrictions have exactly the same form as the rules we originally imposed on Alice.  It is therefore impossible for anybody else to tell which of them made the diagram first, following rules 1-13, and which of them subsequently imposed his or her own lines of constant time and position on the other's diagram.  This symmetry is required by the principle of relativity.

Example:

Let Alice choose her lines of constant time and her lines of constant velocity perpendicular to each other.  Let the lines all be spaced 5 units apart.  Let Bob move with v = 0.2c i with respect to Alice, γ = 1.02.

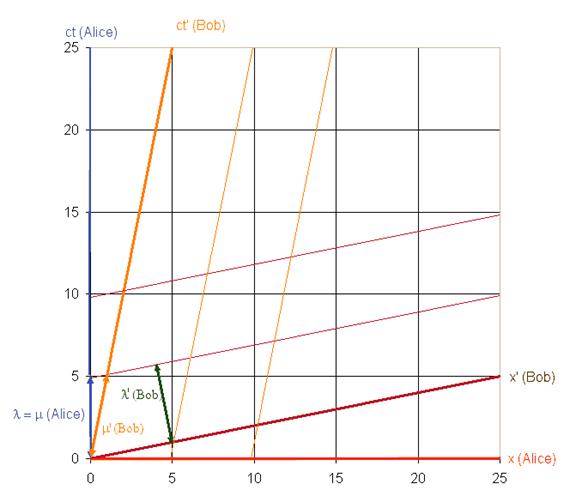
Alice's lines of constant velocity are shown in the diagram. 
The lines are also spaced 5 units apart if Bob's scale factor λ'
 is related to Alice's scale factor λ by
λ'  = λ [(1 - v²/c²)/(1 + v²/c²)]^½.

[Assume the space and time coordinate of an event are 0 in both Alice's and Bob's diagram.  A second event has space coordinate zero in Alice's diagram and time coordinate ct' = 5 units in Bobs diagram.  Its time coordinate t in Alice's diagram is given by ct' = γct, t = t'/γ .  The intersections of Bob's lines of constant time spaced by cΔt' = 5 units intersect Alice's lines of constant position every cΔt'= 5/γ units.
Therefore λ'/(λ/γ ) = cosθ, where tanθ = Δx/Δct = v/c.  Now cosθ = 1/(tan²θ +1)^½,
so λ' = λ[(1 - v²/c²)/(1 + v²/c²)]^½.]

Bob's scale factor μ' is related to Alice's scale factor m by
μ'  = μ[(1 + v²/c²)/(1 - v²/c²)]^½.

The rhombus bounded by lines of constant time and constant position associated with events one unit of ct and one unit of distance apart is a unit rhombus.  The scale factors used by different frames of reference are related by the rule that unit rhombi used by different observers all have the same area. Since the height of a unit rhombus is the scale factor λ and its base is the scale factor μ, the analytical expression of this geometric rule is that for any two frames of reference λ_Aμ_A = λ_Bμ_B.

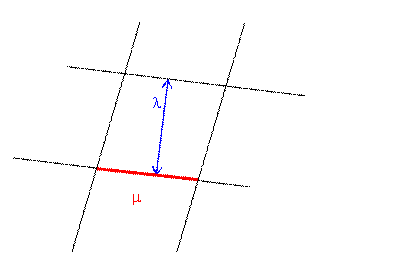
The unit rhombus for some frame of reference.