Electrostatic force, field, potential energy, potential

Point charges

Problem:

Consider 3 positive charges q at the vertices of an equilateral triangle.  Each side has length l.  Find the total force (magnitude and direction) on each of the charges.

Solution:

• Concepts:
  Coulomb's law, F₁₂ = (k_eq₁q₂/r₁₂²) (r₁₂/r₁₂),  k_e = 1/(4πε₀) = 9*10⁹ Nm²/C², the principle of superposition
• Reasoning:
  We are asked to calculate the force exerted on a point charge by other charges.
• Details of the calculation:
  Arrange the charges as shown in the figure.

  

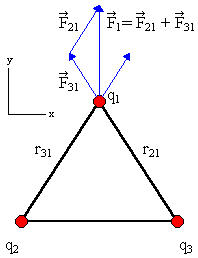
  The force on q₁ is F₁ = F₂₁ + F₃₁ (vector sum).
  The horizontal components of F₂₁ and F₃₁ cancel and the vertical components add.  F₁ points upward, in the y-direction.  The magnitude of F₁ is F₁ = F₂₁cos30^o + F₃₁cos30^o.
  The magnitudes F₂₁ and F₃₁ are given by F₂₁ = F₃₁ = k_eq²/l².
  F₁ = 2 k_e(q²/l²)cos30^o in the y-direction, F₁ = 2 k_e(q²/l²)cos30^o j.
  F₂ and F₃ have the same magnitude.  If F₁ points north, then F₂ points 30^o south of west and F₃ points 30^o south of east.

Problem:

A small negatively charged ball of mass m is suspended on a long insulating string.  An external force very slowly moves another small negatively charged ball on a horizontal path towards the first one from a large distance.  Eventually, the second ball reaches the original location of the first one.  At that moment, the first ball is elevated a small distance h above its original position.  How much work is done by the external force moving the second ball to the original location of the first one?

Solution:

• Concepts:
  Work and energy
• Reasoning:
  The ball moves very slowly, we can neglect radiation.  The work done to the system is equal to the sum of the increase of the gravitational potential energy of the first ball and to the electrostatic potential energy stored in the pair of charged balls.
• Details of the calculation:
  W = ∆U_g + ∆U_e = mgh + k_eq₁q₂/d, where k_e = 1/(4πε₀) and d is the final distance between the balls.
  
  

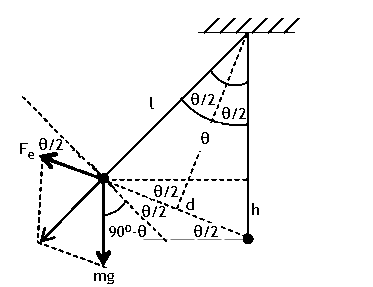
  In equilibrium, the resultant of the weight mg and the Coulomb force along the string is canceled the tension in the string.  The components perpendicular to the string must cancel each other.

  From geometry: 
  (k_eq₁q₂/d²)cos(θ/2) = mgcos(90^o - θ) = mg sinθ = 2mg sin(θ/2)cos(θ/2)
  (k_eq₁q₂/d²) = 2mg sin(θ/2)
  We also have sin(θ/2) = h/d.
  Therefore (k_eq₁q₂/d²) = 2mg h/d,  U_e = k_eq₁q₂/d = 2 mgh.
  W = 3 mgh is the work done by the external agent.

Problem:

A proton is released from rest at a distance of 1 Angstrom from another proton.
(a)  What is the total kinetic energy when the protons have moved infinitely far apart?
(b)  What is the terminal velocity of the moving proton if the other is kept at rest?  If both are free to move, what is their velocity?

Solution:

• Concepts:
  Energy conservation
• Reasoning:
  The Coulomb force is a conservative force.
• Details of the calculation:
  (a)  E = T_final = kq²/r_initial = 9*10⁹*(1.6*10^-19)²/1*10^-10 J = 2.3*10^-18 J = 14.4 eV.
  (b)  If one proton is fixed, the terminal speed of the other proton is v = (2E/m)^1/2 = 5.25*10⁴ m/s.  The free proton moves away from the fixed proton.
  If both protons are free to move, they share the kinetic energy equally.  The speed of each proton is v = (E/m)^1/2 = 3.71*10⁴ m/s.  The protons move away from each other.

Problem:

An alpha particle containing two protons is shot directly towards a platinum nucleus containing 78 protons from a very large distance with a kinetic energy of 1.7*10^-12 J.  The platinum nucleus is held fixed in a matrix.
 What will be the distance of closest approach?

• Concepts:
  Energy conservation
• Reasoning:
  The electrostatic force is a conservative force.  (We are neglecting radiation.)
• Details of the calculation:
  The electric charge of the alpha particle is q₁ = 2q_e and that of the platinum nucleus is q₂ = 78q_e.  The alpha particle and the nucleus repel each other.  As the alpha particle moves towards the nucleus, some of its kinetic energy will be converted into electrostatic potential energy.  At the distance of closest approach, the alpha particle's velocity is zero, and all its initial kinetic energy has been converted into electrostatic potential energy.  The initial kinetic energy of the alpha particle is KE = 1.7*10^-12 J.  The final potential energy is U = kq₁q₂/d, where d is the distance of closest approach. 
  We have k_eq₁q₂/d = 1.7*10^-12 J. 
  This yields
  d = k_eq₁q₂/(1.7*10^-12 J) = (9*10⁹*4*78*(1.6*10^-19)²/(1.7*10^-12)) m = 2.1*10^-14 m
  for the distance of closest approach. 
  The alpha particle's velocity is zero at d.  The acceleration is in a direction away from the nucleus.  The distance between the alpha particle and the nucleus will increase again, converting the potential energy back into kinetic energy.

Problem:

A proton is fired directly at alpha particle (He²⁺) such that the two particles are initially approaching one another with the same (non-relativistic) speed v₀ when they are far apart.  What is the classical distance of closest approach of the two particles?

Solution:

• Concepts:
  Conservation laws
• Reasoning:
  Transforming to the CM frame simplifies the problem.
• Details of the calculation:
  Energy conservation
  In their CM frame the particles approach each other with momenta that have equal magnitudes.
  v_He = 2v₀/5 and v_p = 8v₀/5 in the CM frame.
  At the distance of closest approach d the kinetic energy of both particles has been completely converted into electrostatic potential energy. 
  ½ 3m (2v₀/5)² + ½ m (8v₀/5)² = (8/5)mv₀² = k_e2q_e²/d,
  d = 5k_eq_e²/(4mv₀²) = 5q_e²/(16mπε₀v₀²).   (k_e = 1/(4πε₀)).
  Or:
  Momentum conservation:  4mv₀ - mv₀ = 5mv',  v' = (2/5) v₀
  (At the distance of closest approach the two particles instantaneously move with the same speed v', the speed of the CM.  They have no relative velocity.)
  Change in total energy of the particles:   ΔE = ½ 5m(v₀² - v'²) = (8/5)mv₀² = k_e2q_e²/d.

Problem:

Two point charges +q and -q are connected by a spring with spring constant k and equilibrium length L.
(a)  The system is in equilibrium if the distance between the charges is L/2.  In equilibrium, what is the electric dipole moment p of the system in terms of k and L?
(b)  At large distances away from the system (r >> L) what is the electric field E(r) produced by the system (1st order)?
For the case of p being located at the origin and pointing in the z-direction, write E(r) in terms of spherical coordinates and unit vectors.

Solution:

• Concepts:
  The electric dipole, equilibrium
• Reasoning:
  The dipole moment of a positive point charge q displaced by d with respect to a negative point charge -q is p = qd.
• Details of the calculation:
  (a)  In equilibrium q²/(πε₀L²) = kL/2.  q = (kπε₀L³/2)^½.
  Choose your coordinate system so that the charges lie on the z-axis and place the origin midway between the charges. 
  Then p = qL/2 k = (kπε₀L⁵/8)^½ k.
  (b)  With the midway point located at the origin, the electric field at large distances is E(r) = [1/(4πε₀r³)][3(p·r)r/r² - p].
  With p = p k we have
  E(r) = [p/(4πε₀r³)][2cosθ e_r + sinθ e_θ]
  = [(kπε₀L⁵/8)^½/(4πε₀r³)][2cosθ e_r + sinθ e_θ]
  = (kL⁵/(128πε₀r⁶))^½[2cosθ e_r + sinθ e_θ].

Continuous charge distributions

Problem:

A vertical thin rod of length L carries a total charge Q uniformly distributed.  Calculate the electric field along its axis at a distance z above its top end.

Solution:

• Concepts:
  The electric field due to a charge distribution, the principle of superposition
• Reasoning:
  We are asked to find the electric field due to a line charge distribution.
• Details of the calculation:
  E(z) = k∫_-L⁰ λdz'/(z - z')² = -kλ∫_z+L^z dz''/z''² = kλ(1/z - 1/(z + L)) = kQ/((z + L)z).  E = Ek.

Problem:

Consider a line charge with line charge density λ = Q/2a that extends along the x-axis from x = -a to x = +a.  Find the electric field on the y-axis.

Solution:

• Concepts:
  The electric field due to a charge distribution, the principle of superposition
• Reasoning:
  We are asked to find the electric field due to a line charge distribution.
• Details of the calculation:
  
  The field on the y-axis due to an infinitesimal element of charge λdx is given by
  dE_x = (k_eλdx/(x² + y²)) cosθ,   dE_y = (k_eλdx/(x² + y²)) sinθ,
  where cosθ = x/(x² + y²)^½, sinθ = y/(x² + y²)^½.
  
  On the y-axis the field due to the line charge therefore is given by
  E_x = k_eλ∫_-a^axdx/(x² + y²)^3/2 = 0 from symmetry, and
  E_y = k_eλy∫_-a^adx/(x² + y²)^3/2.
  Using ∫_-a^adx/(x² + y²)^3/2 = 2a/(y²(a² + y²)^½)
  we have  E_y = k_eλ 2a/(y(a² + y²)^½) = k_eQ/(y(a² + y²)^½)
  
  The electric field on the y-axis points in the positive y-direction for y > 0 and in the negative y-direction for y < 0.
  As y becomes very large, we can neglect a² compared to y² under the square root and then E_y = k_eQ/y² ∝ 1/y².  From very far away, the line charge looks like a point charge.
  If, on the other hand, the line is very long, and we y << a, then we can neglect y² compared to a² under the square root and then E_y = k_eQ/(ay) ∝ 1/y.  Near a very long line charge the electric field falls off as 1/distance, not as 1/distance².

Problem:

A disk of radius a carries a non-uniform surface charge density given by σ = σ₀ r²/a², where σ₀ is a constant.
(a)  Find the electrostatic potential at an arbitrary point on the disk axis, a distance z from the disk center and express the result in terms of the total charge Q.
(b)  Calculate the electric field on the disk axis and express the result in terms of the total charge Q.
(c)  Show that the field reduces to an expected form for z >> a.
(d)  To first order in ρ, find an expression for the radial component of  E(ρ, φ, z) at a distance ρ << a away from the z-axis and evaluate it for z >> a.

Solution:

• Concepts:
  The electrostatic potential
• Reasoning:
  We find the electrostatic potential Φ(r) due to a charge distribution using the principle of superposition.
• Details of the calculation:
  (a)  Φ(r) = k ∫_A'σ(r)dA'/|r - r'|
  We are asked to find the potential due to a surface charge distribution in a situation with symmetry.
  dΦ(z) = k2πrσ(r)dr/(r² + z²)^½ = (k2πσ₀/a²)r³dr/(r² + z²)^½ is the potential on the axis due to a ring of radius r. 
  Here k = 1/(4πε₀).
  Φ(z) = (k2πσ₀/a²)∫₀^a r³dr/(r² + z²)^½.
  Q = (2πσ₀/a²)∫₀^a r³dr = ½(kπσ₀a²), therefore Φ(z) = (4Q/a⁴)∫₀^a r³dr/(r² + z²)^½.
  Φ = (4kQ/a⁴)[(1/3)(a² + z²)^3/2 - z²(a² + z²)^½ + 2z³/3].
  (b)  On the axis, the electric field only has a z-component, E = E_z k.
  E_z(z) = -∂Φ/∂z = -(4kQ/a⁴)[-z(a² + z²)^½ - z³(a² + z²)^-½ + 2z²]
  = (4kQ/a⁴)[(z²(1 + a²/z²)^½ + z²(1 + a²/z²)^-½ - 2z²]
  = (4kQz²/a⁴)[(1 + a²/z²)^½ + (1 + a²/z²)^-½ - 2]
  (c)  If z >> a then to 2nd order in a²/z²  we have
  (1 + a²/z²)^½ = [1 + ½a²/z² - (1/8)(a⁴/z⁴)]
  (1 + a²/z²)^-½ = [1 - ½a²/z² + (3/8)(a⁴/z⁴)]
  Therefore to second order [(1 + a²/z²)^½ + (1 + a²/z²)^-½ - 2] = ¼(a⁴/z⁴),
  E_z(z) = kQ/z² = field of a point charge Q.
  (d)  ∇∙E = 0 for z ≠ 0, E has no φ dependence from symmetry.
  In cylindrical coordinates: (1/ρ)∂(ρE_ρ)/∂ρ + (1/ρ) ∂E_φ/∂φ = -∂E_z/∂z.
  E_φ = 0, so ∂(ρE_ρ)/∂ρ = -ρ∂E_z/∂z.
  E_ρ + ρ∂E_ρ/∂ρ = -ρ∂E_z/∂z.
  Near the axis (ρ << a) we expand this expression, keeping only first order tems of the Taylor series.
  E_ρ|_ρ=0 + ∂(E_ρ)/∂ρ|_ρ=0ρ + (ρ∂E_ρ/∂ρ)|_ρ=0 + ∂(ρ∂E_ρ/∂ρ)∂ρ|_ρ=0ρ
  = -(ρ∂E_z/∂z)|_ρ=0 - ∂(ρ∂E_z/∂z)∂ρ|_ρ=0ρ.
  Several tems evaluate to zero,
  ∂(E_ρ)/∂ρ|_ρ=0ρ + ∂E_ρ/∂ρ|_ρ=0ρ =  -∂E_z/∂z|_ρ=0ρ.
  ∂(E_ρ)/∂ρ|_ρ=0 =  -½∂E_z/∂z|_ρ=0.
  E_ρ = ∂(E_ρ)/∂ρ|_ρ=0ρ =  -½∂E_z/∂z|_ρ=0ρ = ½ ρ f(z),
  where f(z) = -∂/∂z[(4kQz²/a⁴)[(1 + a²/z²)^½ + (1 + a²/z²)^-½ - 2]].
  For z >> a, E_ρ = (ρ/z) kQ/z².

Problem:

Charge is distributed uniformly over a thin circular disk of radius R.  The charge per unit area is σ.  Calculate the electric field and potential due to the disk at a point P on the axis of the disk at a distance z away from the center.

Solution:

• Concepts:
  Electrostatics
• Reasoning:
  We are asked to calculate the field and potential for a static charge distribution.
• Details of the calculation:
  Let the disk lie in the xy-plane with its center at the origin.  Then the z-axis is the symmetry axis.
  dV(z) = k2πrσdr/(r² + z²)^½ is the potential on the axis due to a ring of radius r.
  Integrating from r = 0 to r = R we find V(z) = k2πσ{(R²+z²)^½ - z} for a disk of radius R.  Q = σπR², so V(z) = k(2Q/R²)[(R²+z²)^½ - z].
  E_z = -dV(z)/dz = k2πσ[1 - z/(R²+z²)^½].  Symmetry dictates that E = E_zk.

Similar problems

Unknown charge distributions

Problem:

The electric field in some volume V of space is  E = [2A/(x³y²) - By]i + [2A/(x²y³) - Bx]j.
(a)  Show that the line integral of this field over a close path is zero.
(b)  Which charge density ρ in the volume V is consistent with this field?

Solution:

• Concepts:
  Conservative fields
• Reasoning:
  Electrostatic fields are irrotational.  If ∇×E = 0, the line integral of E over any close path is zero.
• Details of the calculation:
  (a)  (∇×E)_x = ∂E_z/∂y - ∂E_y/∂z = 0,  (∇×E)_y = ∂E_x/∂z - ∂E_z/∂x = 0.
  E has no z-component and the x- and y-components do not depend on z.
  (∇×E)_z = ∂E_y/∂x - ∂E_x/∂y = -4A/(x³y³) - B - (-4A/(x³y³) - B) = 0.
  ∇×E = 0, the line integral of E over any close path is zero. (Stokes' theorem)
  (b)  ρ/ε₀  = ∇·E  =  ∂E_x/∂x + ∂E_y/∂y = -6A/(x⁴y²) - 6A/(x²y⁴) = -(6A/(x²y²))(1/x² + 1/ y²)
  ρ = -6Aε₀r²/(x⁴y⁴), with r² = x² + y².