Problem:
A hollow uncharged spherical conducting shell has an inner
radius a and an outer radius b. A positive point charge q
is in the cavity at the center of the sphere.
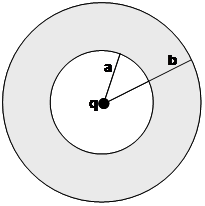
(a) Find the charge on each surface of the conductor
(surface a and surface b).
(b) Find the electric field everywhere.
(c) Find the potential everywhere, assuming that V = 0 at infinity.
Solution:
- Concepts:
Gauss' law, properties of conductors
- Reasoning:
The field due to a spherically symmetric charge distribution can be found from
Gauss' law.
The inside of a conductor is field free in electrostatics.
- Details of the calculation:
(a) Charge on surface a: -q
Charge on surface b: q
(b) 0 < r
< a: E = kq/r2 (r/r)
a < r < b: E = 0
r > b: E = kq/r2 (r/r)
(c) r > b: V = kq/r
a < r < b: V = kq/b
0 < r < a: V = kq/b - kq/a + kq/r = kq(1/r + 1/b - 1/a)
Problem:
A spherical region of space of radius a contains a
charge Q which is uniformly distributed within the volume
(a) Use Gauss's law to determine the magnitude of the
electric field at any radius r from the center of the sphere.
(b) The total electrostatic energy of the sphere may be
calculated from the electric field, using
U = (ε0/2)∫all_space
E·E dV
(SI units).
Evaluate this expression for the uniformly charged sphere.
(c) Calculate the work
required to bring a test charge +q from infinity to the center of the
sphere, using dW = F· dr = +qEdr.
Solution:
- Concepts:
Gauss' law, electrostatic energy
- Reasoning:
A radial field is produced by a
spherically symmetric charge distribution.
- Details of the calculation:
(a) From Gauss' law we have E(r) = Q/(4πε0r2)
for r > a, and E(r) = ρr/(3ε0) for r
< a. Here ρ = 3Q/4πa3.
Therefore E(r) = Qr/(4πa3ε0) for r < a. At r = 0 we have E(r) = 0.
(b) U = (4πε0/2)[ ∫0ar2dr
Q2r2/(4πa3ε0)2
+ ∫a∞r2dr
Q2/(4πε0r2)2]
= (Q2/(8πε0))[ ∫0ar4dr/a6
+ ∫a∞dr
/r2] = [Q2/(8πε0)][1/(5a)
+ 1/a] = (3/5) Q2/(4πε0a).
(c) W = q[∫0adr Qr/(4πa3ε0)
+ ∫a∞dr Q/(4πε0r2)] =
[qQ/(4πε0)][1/(2a) +
1/a]
= 3qQ/(8πε0
a).

