Uniqueness theorem, boundary conditions, boundary value problems
Uniqueness theorem
Problem:
Prove, carefully explaining your reasoning, that the solution of
∇∙E = ρ/ε0, ∇×E = 0, for
E is unique. You may assume that the sources of
E are bounded in
space and that therefore the field vanishes at sufficiently large distances from the
sources.
Solution:
- Concepts:
The uniqueness theorem, Green's first identity
∫V
(Φ∇2ψ +
∇Φ∙∇ψ)
dV = ∮S Φ(∂ψ/∂n) dS
Green's first identity is derived starting with Green's theorem:
∫V∇∙A dV = ∮S A∙n dS
Set A = Φ∇ψ, with Φ, ψ arbitrary scalar fields.
∇∙A =
∇∙(Φ∇ψ)
= Φ∇2ψ
+ ∇Φ∙∇ψ
A∙n = Φ∇ψ∙n = Φ(∂ψ/∂n)
- Reasoning:
We are asked to prove the uniqueness theorem.
- Details of the calculation:
∇×E = 0 <==>
E = -∇Φ,
E is the gradient of some scalar function.
∇·E = ρ/ε0
<==> ∇2Φ = -ρ/ε0.
Consider the volume V bounded by surfaces at infinity. Assume we
know ρ(r) everywhere inside V and we know
that Φ = 0 at the boundaries.
Assume that two solutions for Φ exist that
satisfy the same boundary conditions.
∇2Φ1
= -ρ/ε0, ∇2Φ2
= -ρ/ε0.
Let U = Φ1 - Φ2,
then ∇2U = 0 and U = 0 at the
boundaries.
Apply Green's first identity with Φ = ψ
= U.
∫V
(U∇2U +
∇U∙∇U)
dV = ∮S
U(∂U/∂n) dS
The right hand side is zero. ∇2U
= 0. Therefore
∫V| ∇U|2 dV = 0.
Since |∇U|2 is a non-negative
everywhere, this implies ∇U = 0
everywhere inside V and U is constant. Φ1 and Φ2 differ at most by a
constant. This constant is zero since Φ1 = Φ2 at the boundaries.
Φ
is unique, E = -∇Φ is unique.
Boundary value problems, azimuthal symmetry
Problem:
A sphere of radius R carries a surface charge density
σ = σ0cosθ.
(a) Derive the exact potential everywhere (both inside and
outside the sphere) assuming that it vanishes as r goes to infinity.
(b) Calculate the dipole moment of the charge distribution and
deduce the approximate form of the potential at points far from the sphere (r >> R).
(c) Compare (a) and (b). What can you conclude about the higher
multipoles?
Solution:
- Concepts:
Boundary value problems,
Φ(r,θ) = ∑n=0∞[Anrn
+ Bn/rn+1]Pn(cosθ)
is
the general solution to Laplace's equation for problems with azimuthal
symmetry.
- Reasoning:
Φ(r,θ) = ∑n=0∞[Anrn
+ Bn/rn+1]Pn(cosθ) is the most general solution
inside and outside of the sphere, since ρ = 0
inside and outside of the sphere. To find the specific solution we
apply boundary conditions.
- Details of the calculation:
Assume Φ1(r,θ)
= ArP1(cosθ) = Arcosθ
inside the sphere and Φ2(r,θ)
= (B/r2)P1(cosθ) = (B/r2)cosθ
outside the sphere. The symmetry of the situation suggests this form
of the solution. If we can satisfy the boundary conditions, the
uniqueness theorem guaranties that we have found the only solution.
The potential vanishes as r goes to infinity.
Boundary conditions:
Φ is continuous across the boundary. Φ1(R,θ) = Φ2(R,θ).
A = B/R3.
(E2 - E1)·n2
= σ/ε0, dΦ2/dr
- dΦ1/dr|R = -σ/ε0.
-2(B/R3)cosθ - Acosθ
= -σ0cosθ/ε0.
-2A -A = -σ0/ε0.
A = σ0/3ε0.
Φ1(r,θ) = (σ0/3ε0) r cosθ
inside the sphere and Φ2(r,θ)
= (σ0R3/3ε0r2)cosθ
outside the sphere.
(b) dipole moment: p = ∫σ(r)r
dA = k σ0∫cosθ Rcosθ 2πR2sinθdθ
= k σ0(4π/3)R3.
dipole potential: Φdip = (1/(4πε0))p∙r/r3
= (σ0R3/3ε0r2)cosθ.
The potential outside the sphere is a pure dipole potential. The
higher multipoles are zero.
Problem:
A hollow ball of radius R has a surface charge distribution which produces a
potential on the surface of V(R,θ) = k(cos2θ + 1), where k is a
constant and θ is the usual polar angle relative to the z-axis.
(a)
Find the potential at all points in space.
(b) Show that the charge
distribution on the ball is σ(R,θ) = (kε0/R)(5cos2θ -
(1/3)).
Solution:
- Concepts:
General
solution to Laplace's equation in situations with azimuthal symmetry,
boundary value problems
- Reasoning:
Φ(r,θ) = ∑n=0∞[Anrn
+ Bn/rn+1]Pn(cosθ)
is the
most general solution inside and outside of the sphere, since ρ = 0 inside
and outside of the sphere. To find the specific solution we apply boundary
conditions. The potential on the surface of the ball is given.
- Details of the calculation:
(a) Assume
Φ1(r,θ) = A0
+ A2r2P2(cosθ) inside the sphere and
Φ2(r,θ)
= (B0/r) + (B2/r3)P2(cosθ)
outside the sphere.
The symmetry of the situation suggests this form of
the solution. If we can satisfy the boundary conditions, the uniqueness
theorem guaranties that we have found the only solution. The potential
vanishes as r goes to infinity.
Boundary conditions:
Φ1(r,θ)
is finite at r = 0 and Φ2(r,θ) goes to zero as r goes to
infinity.
Φ is continuous across the boundary at r = R.
A0
= B0/R, A2 = B2/R5.
Φ(R,θ)
= A0 + A2R2P2(cosθ) = A0
+ A2R2(3cos2θ -1)/2 = k(cos2θ +
1).
3A2R2/2 = k, A0 - A2R2/2
= k, A2 = 2k/(3R2), A0 = 4k/3.
Φ1(r,θ)
= 4k/3 + (2k/(3R2))r2P2(cosθ), Φ2(r,θ)
= 4kR/(3r) + (2kR3/(3r3))P2(cosθ) .
(b)
(E2 - E1)·n2
= σ/ε0, ∂Φ2/∂r
- ∂Φ1/∂r |R = -σ/ε0.
∂Φ2/∂r =
-4kR/(3r2) - (2kR3/r4)P2(cosθ),
∂Φ1/∂r = (4k/(3R2))rP2(cosθ).
σ(R,θ)/ε0
= 4k/(3R) + (2k/R)P2(cosθ) + (4k/(3R))P2(cosθ)
=
4k/(3R) + 10k/(3R))P2(cosθ).
σ(R,θ) = (kε0/R)(4/3 +
(10/3)(3cos2θ - 1)/2) = (kε0/R)(5cos2θ -
(1/3)).
Problem:
Consider a hollow sphere of radius R with a surface
potential Φ(R,θ) = k sin2θ, where k is a constant and θ is the usual
polar angle relative to the z-axis.
Find the potential everywhere inside the sphere.
Hint:
P0(x) = 1
P1(x) = x
P2(x) = (3x2 - 1)/2
P3(x) = (5x3 - 3x)/2
Solution:
- Concepts:
General solution to Laplace's equation in
situations with azimuthal symmetry, boundary value problems
- Reasoning:
Φ(r,θ) = ∑n=0∞[Anrn
+ Bn/rn+1]Pn(cosθ)
is the most general solution inside and
outside of the sphere, since ρ = 0 inside and outside of the sphere. To find
the specific solution we apply boundary conditions. The potential on the
surface of the sphere is given.
- Details of the calculation:
Φ(R,θ) = k sin2θ = k(1 - cos2θ) = (2k/3)(P0
- P2(cosθ)).
Assume
Φ1(r,θ) = A0 + A2r2P2(cosθ)
inside the sphere.
The symmetry of the situation suggests this form of the solution. If we can
satisfy the boundary conditions, the uniqueness theorem guaranties that we have
found the only solution.
Boundary conditions:
Φ1(r,θ) is finite at r = 0 .
Φ is continuous across the boundary at r = R.
A0 = 2k/3, A2R2 = -2k/3.
Φ1(r,θ) = 2k/3 - (2k/3)(r2/R2)P2(cosθ)
= 2k/3 - (2k/3)(r2/R2)( 1 - (3/2)sin2θ)
is the potential inside the sphere.
Problem:
A conducting sphere of radius a is located in an electric field that is
uniform at infinity, i.e. E = E0
k at infinity.
Put the origin of the coordinate system at the center of a sphere and set the
potential Φ(0) = 0.
Solve for the electric potential and the electric field everywhere by
boundary value methods.
Solution:
- Concepts:
Most general solution to Laplace's equation, boundary conditions
- Reasoning:
Φ1 = 0, E1 = 0 inside the sphere since the
interior of a conductor in electrostatics is field-free. ∇2Φ2
= 0 and outside the sphere since ρ = 0 outside the sphere. We are looking
for a solution for ∇2Φ2 = 0, subject to the boundary
conditions.
- Details of the calculation:
We have azimuthal symmetry.
Φ(r,θ) = ∑n=0∞[Anrn + Bn/rn+1]Pn(cosθ)
is the most general solution of ∇2Φ = 0 for problems with
azimuthal symmetry.
Assume Φ1 = 0 inside, Φ2 = A0' + A1'rcosθ
+ B0'/r + (B1'/r2)cosθ outside.
We assume all higher-order coefficients are zero. If we find a solution
with this assumption, it is the only solution.
Boundary conditions:
(i) Φ is continuous at r = a . 0 = A1'a + B1'/a2.
(ii) E2 = E0 at r >> a.
-A1'cosθ = E0cosθ, A1'sinθ = -E0sinθ,
A1' = -E0, B1' = E0a3.
Φ2 = -E0rcosθ + (E0a3/r2)cosθ.
E2 = -∇Φ2.
E2r = E0cosθ + 2(E0a3/r3)cosθ,
E2θ = -E0'sinθ + (E0a3/r3)sinθ.
E2 = E0 + 2(E0a3/r3)cosθ
(r/r) + (E0a3/r3)sinθ (θ/θ).
E2 = external field + field due to the polarized sphere.
Problem:
Two thin wires, each of length L, lie on the z-axis. Wire 1 has a positive
charge per unit length +λ and extends from (0, 0, L) to (0,0,0). Wire 2 has a
negative charge per unit length -λ and extends from (0,0,0) to (0,0,-L).
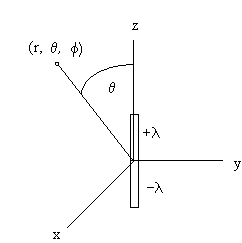
(a) Find the potential Φ on the z-axis at z > L.
(b) The potential Φ(r,θ) at arbitrary points in space with r > L can be
expanded in terms of Legendre polynomials, Φ(r,θ) = ∑n=0∞[Anrn
+ Bn/rn+1]Pn(cosθ).
Find the expansion coefficients.
Note: ln(1 + x) = ∑n=1∞(-1)n+1xn/n
Solution:
- Concepts:
Symmetry, Φ(r,θ) = ∑n=0∞[Anrn
+ Bn/rn+1]Pn(cosθ) is the
general solution to Laplace's equation for problems with azimuthal symmetry.
- Reasoning:
Φ(r) = [1/(4πε0)]∫ρ(r')dV'/|r -
r'|.
We can evaluate this integral for r = rk.
For r > L, Φ(r) satisfies Laplace's equation, ∇2Φ(r) =
0. The general solution is
Φ(r,θ) = ∑n=0∞[Anrn + Bn/rn-1]Pn(cosθ).
We can find the coefficients by comparing the general solution to the solution
found by integration on the z-axis.
- Details of the calculation:
(a) Φ(z) = [1/(4πε0)]∫0Lλdz'/(z -
z') -
[1/(4πε0)] ∫-L0λdz'/(z -
z')
= [1/(4πε0)][-λ∫zz-Ldx/x + λ∫z+Lzdx/x]
= [1/(4πε0)] [-λln((z - L)/z) + λln(z/(z + L))]
= -[λ/(4πε0)]ln[(z2 - L2)/z2].
Φ(z) = -[λ/(4πε0)]ln(1 - u), with u = L2/z2.
(b) For r > L ∑n=0∞(Bn/rn+1)Pn(cosθ).
Only the odd parity terms contribute and all An are zero since Φ = 0
at infinity.
We can therefore write Φ(r,θ) = ∑n=1∞(B2n-1/r2n)P2n-1(cos(θ)).
On the positive z-axis Φ(z) = ∑n=1∞(B2n-1/z2n),
since Pn(1) = 1.
Expanding ln(1 - u) = ∑n=1∞(-1)n+1(-u)n/n
we have, equating the two expressions for Φ(z),
∑n=1∞(B2n-1/z2n) = -[λ/(4πε0)]
∑n=1∞(-1)n+1(-u)n/n = [λ/(4πε0)]
∑n=1∞(-1)2n+2un/n
= [λ/(4πε0)] ∑n=1∞L2n/(nz2n).
Equating term with equal powers of z we have B2n-1/z2n =
[λ/(4πε0)] L2n/(nz2n).
B2n-1 = [λ/(4πε0)] L2n/n.
Φ(r,θ) = ∑n=1∞([λ/(4πε0)] L2n/n)(1/r2n)P2n-1(cos(θ)).
Problem:
A charge array consists of two charges, each of magnitude +q, located on the
z-axis at (0, 0, ±a).
(a) Find the potential V(0,0,z) at an arbitrary
point z > a; then expand V(0, 0,z) in a power series in z.
(b) Using
this series as a "boundary condition", find the potential V(r,θ,φ) at an
arbitrary location (r,θ,φ) with r > a. An infinite series is acceptable.
(c) Characterize the first three terms in 1/rn.
Solution:
- Concepts:
The electrostatic potential
- Reasoning:
In regions with charge density ρ = 0 we have ∇2V
= 0. So in the region r > a we have
∇2V = 0. For a problem
with azimuthal symmetry, the most general solution for ∇2V = 0
is
V(r,θ) = Σn=0∞(Anrn + Bnr-(n+1))Pn(cosθ).
On the positive z-axis Pn(cosθ) = 1 and V(z) = Σn=0∞(Anzn
+ Bnz-(n+1)).
If we know the potential on the
z-axis, we can solve for the expansion coefficients by equating term of
equal power in z.
- Details of the calculation:
(a) V(z) = kq/(z - a) + kq/(z + a) =
(kq/z)[(1 - a/z)-1 + (1 + a/z)-1].
Assume a/z < 1.
For x < 1 we have (1 ± x)-1 = 1 ∓ x + x2 ∓ x3
+ ... .
V(z) = (2kq/z)(1 + (a/z)2 + (a/z) 4 + ...) =
2kq(1/z + a2/z3 + a4/z 5 + ...).
(b) V(z) = 2kq(1/z + a2/z3 + a4/z 5
+ ...) = Σn=0∞(Anzn + Bnz-(n+1)).
An = 0 for all n. Bn = 0 for n = odd, Bn
= 2kqan for n = even.
V(r,θ) = 2kqΣn=even anr-(n+1)Pn(cosθ).
(c) First term: Monopole term ∝ 1/r = 2kq/r.
Second term: Dipole
term ∝ 1/r2 = 0.
Third term: Quadrupole term ∝ 1/r3
= 2kqa2P2(cosθ)/r3.
Boundary value problems, other symmetry
Problem:
A rectangular box occupying the region 0 ≤ x ≤ A, 0 ≤ y ≤ B, 0 ≤ z ≤ C, has
an electrostatic potential V(x,y,z) = 0 on all faces except the face z =
C, where the potential is V0. Starting from Laplace's equation,
find the potential V everywhere inside.
Solution:
- Concepts:
General solution to Laplace's equation, boundary conditions
- Reasoning:
ρ = 0 inside the box, ∇2V = 0 inside the box.
- Details of the calculation:
In Cartesian coordinates ∇2V = ∂2V/∂x2
+ ∂2V/∂y2 + ∂2V/∂z2
= 0.
Separation of variables: V(x,y,z) = F1(x)F2(y)F3(z).
(1/F1)∂2F1/∂x2 + (1/F2)∂2F2/∂y2
+ (1/F3)∂2F3/∂z2 = 0.
Since each term in the sum is a function of a different independent variable,
each term must be equal to a constant and the constants have to sum to zero.
Let (1/F1)∂2F1/∂x2 = -a2, ∂2F1/∂x2
+ a2F1 = 0.
(1/F2)∂2F2/∂y2
= -b2, ∂2F2/∂y2 +
b2F2 = 0.
(1/F3)∂2F3/∂z2 = (a2
+ b2), ∂2F3/∂z2 -
(a2 + b2)F3 = 0.
Solutions that can fulfill the boundary conditions on all faces require
F1(x) = sin(ax), a = nπ/A, F2(y) = sin(by), b = mπ/B,
n, m = 1. 2, 3, ... .
F3(z) = sinh(cz) c = π(n2/A2 + m2/B2)½.
The solution is
V(x,y,z) = ∑n=1∞∑m=1∞Dnmsinh(cnmz)
sin(nπx/A) sin(mπy/B),
subject to the boundary condition V(x,y,C) = V0.
If p, q = odd then ∫0Adx∫0Bdy V0sin(pπx/A)
sin(qπy/B) = [4V0AB/(pqπ2)]
[V0AB/(pqπ2)] = Dpqsinh(cpqC)
¼AB.
Therefore Dnm = 16V0/(nmπ2sinh(cnmC)),
n, m = odd.
Problem:
Semi-infinite planes at φ = 0 and φ = π/6 are separated by an infinitesimal
insulating gap as shown in the figure. For V(φ = 0) = 0 and V(φ = π/6) =
100 V, calculate V and E in the region between the plates.
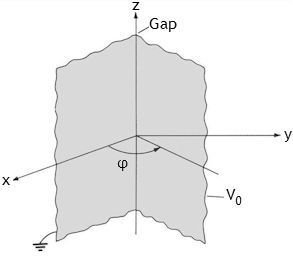
Solution:
- Concepts:
Laplace's equation in cylindrical coordinates
- Reasoning:
Since the plates are semi-infinite, V can only depend on φ.
∇2V = (1/ρ)∂/∂ρ(ρ∂V/∂ρ) + (1/ρ2)∂2V/∂φ2
+ ∂2V/∂z2 = 0 becomes
(1/ρ2)∂2V/∂φ2 = 0.
Since ρ = 0 is excluded due to the insulating gap, we can write ∂2V/∂φ2
= 0.
- Details of the calculation:
Integrating twice gives V = Aφ + B.
Boundary conditions:
V(φ = 0) = 0 --> B = 0.
V(φ = π/6) = 100 V --> A = 600 V/π.
Therefore V(φ) = 600*(φ/π) V between the plates.
E = -∇V = -(1/ρ)∂V/∂φ (φ/φ) = 600/(ρπ) V/m
with ρ measured in m.
Problem:
A long cylinder of radius a and relative permittivity ε carries a free surface
charge density σf = σ0cos2(φ).
(a) Find the potential Φ inside and outside of the cylinder.
(b) Find the electric field E inside and outside the cylinder.
(c) Find the polarization surface charge density of the cylinder.
Let
Φ = Φ(ρ,φ), 0 ≤ θ ≤ 2π in
cylindrical coordinates.
Then the most general solution for ∇2Φ =
0 is
Φ(ρ,φ) = ∑n=1∞(Ancos(nφ)
+ Bnsin(nφ))ρn + ∑n=1∞(A'ncos(nφ)
+ B'nsin(nφ))ρ-n + a0 + b0lnρ.
Solution:
- Concepts:
Boundary value problems,
Φ(ρ,φ) = ∑n=1∞(Ancos(nφ)
+ Bnsin(nφ))ρn + ∑n=1∞(A'ncos(nφ)
+ B'nsin(nφ))ρ-n + a0 + b0lnρ
- Reasoning:
Φ = Φ(ρ,φ) (0 ≤ φ ≤ 2π) independent
of z. The problem involves the whole azimuthal range.
- Details of the calculation:
(a) σ = σ0cos2(φ) = σ0(½
+ ½cos(2φ)).
Assume Φ1(ρ,φ) = A2cos(2φ)ρ2
inside,
Φ2(ρ,φ) = A'2cos(2φ)ρ-2 + a0 + b0lnρ
outside.
We assume all other coefficients are zero. If we find a solution
with this assumption, it is the only solution.
Boundary conditions:
ρ < a: Φ is finite at the origin. We choose Φ(0) = 0.
ρ = a:
Φ is continuous, A2cos(2φ)a2 = A'2cos(2φ)a-2 + a0 + b0lna.
A2a4 = A'2, a0 =
-b0lna.
(D2 - D1)·n2
= σf at ρ = a.
(D2 - D1)∙(ρ/ρ) = σ0(½
+ ½cos(2φ)) at ρ = a.
Eρ1 = -∂Φ1/∂ρ = -2A2cos(2φ)ρ,
Eρ2 = -∂Φ2/∂ρ = 2A2cos(2φ)ρ-3
- b0/ρ.
Dρ1 = -ε2A2cos(2φ)ρ, Dρ2
= ε02A2a4cos(2φ)ρ-3 - ε0b0/ρ.
(ε0 + ε)2A2cos(2φ)a - ε0b0/a = σ0(½
+ ½cos(2φ)).
A2 = σ0/(4a(ε0 + ε)), b0
= -aσ0/2ε0.
Φ1(ρ,φ) = σ0/cos(2φ)ρ2/(4a(ε0
+ ε)).
Φ2(ρ,φ) = a4σ0cos(2φ)ρ-2/(4a(ε0
+ ε)) - (½aσ0/ε0)ln(ρ/a).
(b) E = -∇Φ.
Eρ = ∂Φ/∂ρ, Eφ = (1/ρ)∂Φ/∂φ.
Ein = -2A2cos(2φ)ρ [ρ/ρ] + 2A2sin(2φ)ρ2
[φ/φ]
= -σ0cos(2φ)ρ/(2a(ε0 + ε)) [ρ/ρ] + σ0sin(2φ)ρ2/(2a(ε0
+ ε))
[φ/φ].
Eout = (2A2a4cos(2φ)ρ-3
- b0/ρ)[ρ/ρ] + 2A2a4sin(2φ)ρ-2
[φ/φ]
= (σ0a4cos(2φ)ρ-3/(2a(ε0
+ ε)) + aσ0/(2ε0ρ) [ρ/ρ] +
σ0a4sin(2φ)ρ-2/(2a(ε0
+ ε))
[φ/φ].
(c)
(E2 - E1)·[ρ/ρ]
= (σf + σp)/ε0 at ρ = a.
σ0cos(2φ)/(2(ε0 + ε)) + σ0/(2ε0)
+ σ0cos(2φ)/(2(ε0 + ε))
= σ0cos(2φ)/(ε0 + ε) + σ0/(2ε0)
= (σf + σp)/ε0 .
σp = ε0σ0cos(2φ)/(ε0 + ε)
- σ0½cos(2φ) = ½(ε0 - ε)σ0cos(2φ)/(ε0 + ε).
Or =
σp = P·[ρ/ρ] evaluated at ρ = a.
P = ε0χeEin = (ε0
- ε0)Ein,
σp = ½(ε0 - ε)σ0cos(2φ)/(ε0 + ε).

