Kinematics (electric force)

Problem:

An electron is released from rest at one point in a uniform electric field and moves a distance of 10 cm in 10^-7 s.  What is the electric field strength and what is the voltage between the two points?

Solution:

• Concepts:
  Kinematics, the electrostatic force, F = qE.
• Reasoning:
  Kinematics lets us solve for a, F = ma = qE yields E.
• Details of the calculation:
  Δx = ½at²,  a = 2*Δx/t² = (2*0.1/10^-14) m/s².
  qE = ma, E = ma/q = 9.1*10^-31*2*10¹³/(1.6*10^-19) N/C = 113.75 V/m
  The voltage between the points is 11.375 V.

Problem:

A proton is accelerated, in vacuum, from rest through a potential U and directed horizontally at a point midway between two horizontal parallel plates which are separated by 0.80 cm and 5 cm long.  An electric field is established between the plates by a 10 kV voltage supply and causes downward deflection.  Find the minimum accelerating potential U that will avoid the proton striking the lower plate.

Solution:

• Concepts:
  Projectile motion
• Reasoning:
  The acceleration in the horizontal direction is zero and the acceleration in the vertical direction is constant.
• Details of the calculation:
  a_x = 0, v_x = v₀, mv₀²/2 = q_eU,  x = v₀t.
  a_y = (q_eV/md), y = a_yt²/2.
  The proton just 'clips' lower plate when a_yt²/2 = d/2 or t = (d/a_y)^½  and simultaneously t = L/v₀, with d = separation and L = length of plates. 
  d/a_y = L²/v₀² = mL²/(2q_eU).  md²/(q_eV) = mL²/(2q_eU).  d²/V = L²/2U. 
  The critical value of U is U = (L²/d²)(V/2). 
  The minimum U that will avoid striking the lower plate is then (5/0.8)²(5 kV) = 195 kV.

Problem:

A Wideroe linear accelerator consists of a series of cylinders connected to an alternating voltage.  A charged particle is accelerated during its passage through the gaps between the cylinders.  Inside the cylinders there is no acceleration.  The gaps all have equal lengths d, but the lengths of the cylinders, which are much longer than d, are chosen so that particles arrive at the gaps at the right phase of the alternating voltage to be accelerated.  Let there be N cylinders.  Find the length of the nth cylinder for a proton to be accelerated to the energy of 100 MeV if the frequency of the accelerating voltage is 150 MHz and if the acceleration across each gap is assumed to be constant. 

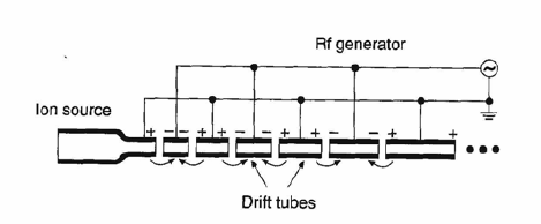
Solution:

• Concepts:
  Kinematics
• Reasoning:
  The particle is accelerated in gaps of equal length.  This is a non-relativistic problem, E << mc².
• Details of the calculation:
  Let d be the width of each gap and l = nd be the length of the region through which the particle has been accelerated when its velocity is v.  Let a be the acceleration, a = qE/m = qV/(dm).
  v² = 2al.
  Since l = nd, we have v_n² = n2ad = n2qV/m.  Here v_n is the speed of the particle after the nth gap.
  The length of the nth section is L_n = v_nT/2, where T is the period of the AC voltage.
  L_n² = nqVT²/(2m).
  If there are N cylinders then NV = 100MV.  T = 1/f = (1/1.5*10⁸)s.
  L_n² = (n/N)100*1.6*10^-13Js²/[(1.5*10⁸)²*2*1.67*10^-27kg]
  L_n = (n/N)^½*46.1 cm