Boundary value problems with dielectrics

Problem:

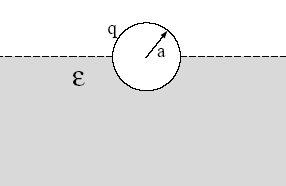
A conducting sphere of radius a carrying a charge q is submerged halfway into a non-conducting dielectric liquid of dielectric constant ε.  The other half is in air. 
Will the electric field be purely radial?  Explain.

Solution:

• Concepts:
  Boundary value problems, the uniqueness theorem
• Reasoning:
  There are no free charges except on the boundaries and the problem has azimuthal symmetry.
• Details of the calculation:
  If we place the origin of our coordinate system at the center of the sphere and let the z-axis point upward, then the problem has azimuthal symmetry.  We have 3 regions.
  Region 1: the sphere
  Region 2: the air
  Region 3: the dielectric
  In region 1 E = 0 and Φ = constant (properties of conductors).
  Assume that in regions 2 and 3 Φ(r) = C/r, with C a constant.
  This potential fulfills all the boundary conditions.
  Φ = constant at r = a, Φ --> 0 as r --> infinity, Φ = continuous across the air-dielectric interface, and the normal component of D is continuous across the air-dielectric interface.  The uniqueness theorem guaranties that this solution is the only solution.  E = -∇Φ, the electric field will be purely radial.  E will only depend on r.
  Think about:  What is the value of the constant C?
  Outside the sphere in the dielectric at r = a:  E = (σ_f3 + σ_p)/ε₀ = (σ_f3 - P)/ε₀ = (σ_f3 - ε₀x_eE)/ε₀.
  σ_f3 = ε₀(1 + x_e)E = εE.
  Outside the sphere in air at r = a:  E = σ_f2/ε₀,  σ_f2 = ε₀E.
  2πa²E(ε + ε₀) = q.  E = q/(2π(ε + ε₀)a²), 
  C = q/(2π(ε + ε₀)a²).

Azimuthal symmetry

Problem:

A dielectric sphere of radius a has a uniform isotropic permittivity, kε₀, and is located in an electric field that is uniform at infinity.
(a)  Solve for the electric potential everywhere by boundary value methods.
(b)  Show that the electric field inside the sphere is uniform and find its value relative to the field E₀ at infinity.

Solution:

• Concepts:
  Most general solution to Laplace's equation, boundary conditions
• Reasoning:
  ∇²Φ = 0 inside and outside the sphere since ρ_f = 0 inside and outside the sphere.  We are looking for a solution for ∇²Φ = 0, subject to the boundary conditions.
• Details of the calculation:
  We have azimuthal symmetry.
  Φ(r,θ) = ∑_n=0^∞[A_nrⁿ + B_n/rⁿ⁺¹]P_n(cosθ).
  Assume Φ₁ = A₀ + A₁rcosθ + B₀/r + (B₁/r²)cosθ inside,
  Φ₂ = A₀' + A₁'rcosθ + B₀'/r + (B₁'/r²)cosθ outside.
  We assume all higher-order coefficients are zero.  If we find a solution with this assumption, it is the only solution.
  Boundary conditions:
  (i)  Φ₁ is finite at the origin, B₀ = B₁ = 0.  Φ₁ = A₀ + A₁rcosθ.
  E₁ = -∇Φ₁,  E_1r = -A₁cosθ,  E_1θ = A₁sinθ,  E₁ = -A₁k.
  D₁ = εE₁ = kε₀E₁.
  (ii)  Φ is continuous at r = a.  A₀ = A₀' + B₀'/a,  A₁a = A₁'a + B₁'/a².
  (iii)  The radial component of D is continuous at r = a.  (There are no free charges.)
  E₂ = -∇Φ₂.  E_2r = -A₁'cosθ + B₀'/r² + 2(B₁'/r³)cosθ,  E_2θ = A₁'sinθ + (B₁'/r³)sinθ,
  D₂ = ε₀E₂.
  -kε₀A₁cosθ = -ε₀A₁'cosθ + ε₀B₀'/a² + 2ε₀(B₁'/a³)cosθ.
  B₀' = 0, kA₁ = A₁' - 2(B₁'/a³) = A₁' - 2(A₁ - A₁').
  (iv)  E = E₀ at r >> a.
  -A₁'cosθ = E₀cosθ,  A₁'sinθ = -E₀sinθ,  A₁' = -E₀.
  A₁ = 3A₁'/(k + 2) = -3E₀/(k + 2).
  B₁' =[(k - 1)/(k + 2)]E₀a³.
  A₀ = A₀' is an arbitrary constant.  We choose this constant to be zero.  A₀ = A₀' = 0.
  Φ_inside = -(3E₀/(k + 2))rcosθ = -3E₀z/(k + 2), 
  Φ_outside = -E₀rcosθ + [(k - 1)/(k + 2)](a³/r²)E₀cosθ.
  
  (b)  E_in = -∇Φ_in = 3E₀/(k + 2).

Problem:

Consider a homogeneous dielectric ε, of infinite extent, in which there is a uniform field E₀.  A spherical cavity of radius a is cut out of this dielectric.  Find:
(a)  Φ in the cavity and on its surface.
(b)  The polarization charge density σ_p on the walls.
(c)  The field outside the cavity.

Solution:

• Concepts:
  Boundary value problems,  Φ(r,θ) = ∑_n=0^∞[A_nrⁿ + B_n/rⁿ⁺¹]P_n(cosθ) is the general solution to Laplace's equation for problems with azimuthal symmetry.
• Reasoning:
  Let the center of the cavity be at the origin.  Then the problem has azimuthal symmetry.
  Φ(r,θ) = ∑_n=0^∞[A_nrⁿ + B_n/rⁿ⁺¹]P_n(cosθ) is the most general solution inside and outside of the cavity, since r = 0 inside and outside of the cavity.  To find the specific solution we apply boundary conditions.
• Details of the calculation:
  (a)  Assume Φ₁ = A₀ + A₁rcosθ + B₀/r + (B₁/r²)cosθ inside,
  Φ₂ = A₀' + A₁'rcosθ + B₀'/r + (B₁'/r²)cosθ outside.
  We assume all higher-order coefficients are zero.  If we find a solution with this assumption, it is the only solution.
  Boundary conditions:
  (i)  E₂ = E₀ at r >> a,  Φ₂ = -E₀z = -E₀rcosθ  at r >> a,  A₁' = -E₀,  we choose A₀' = 0.
  Then, from symmetry, A₀ = 0.
  (ii)  Φ₁ is finite at the origin, B₀ = B₁ = 0.  Φ₁ = A₁rcosθ,  
  E₁ = -∇Φ₁,  E_1r = -A₁cosθ,  E_1θ = A₁sinθ,  E₁ = -A₁k.
  D₁ = ε₀E₁.
  (iii)  Φ is continuous at r = a.  B₀' = 0,  A₁a = -E₀a + B₁'/a².
  (iv)  The radial component of D is continuous at r = a.  (There are no free charges.)
  E₂ = -∇Φ₂.  E_2r = -A₁'cosθ + 2(B₁'/r³)cosθ,  E_2θ = A₁'sinθ + (B₁'/r³)sinθ,  D₂ = kε₀E₂ = eE₂.
  -ε₀A₁cosθ = kε₀E₀cosθ + 2kε₀(B₁'/a³)cosθ.
  A₁ = -kE₀ - 2k(B₁'/a³) = -kE₀ - 2k(A₁ + E₀).
  A₁ = -3E₀k/(2k + 1) = -3E₀ε/(ε₀ + 2ε).
  B₁' = [(ε₀ - ε)/(ε₀ + 2ε)]E₀a³.
  Φ₁ = [-3E₀ε/(ε₀ + 2ε)]rcosθ.
  On the surface Φ(a) = [-3E₀ε/(ε₀ + 2ε)]acosθ.
  
  (b)  σ_p = ε₀(E_2r(a)- E_1r(a) ) = ε₀E₀cosθ[1 + 2(ε₀ - ε)/(ε₀ + 2ε) + 3ε/(ε₀ + 2ε)]
  σ_p = ε₀E₀cosθ[1 + (2ε₀ + ε))/(ε₀ + 2ε)] = ε₀E₀cosθ[3(ε₀ + ε))/(ε₀ + 2ε)].
  
  (c)  Φ₂ = -E₀rcosθ + [(ε₀ - ε)/(ε₀ + 2ε)]E₀a³cosθ/r²,
  E_2r = -∂Φ₂/∂r = E₀cosθ[1 + 2[(ε₀ - ε)/(ε₀ + 2ε)]a³/r³],
  E_2θ = -(1/r)∂Φ₂/∂θ = -E₀sinθ[1 - [(ε₀ - ε)/(ε₀ + 2ε)]a³/r³].

Problem:

A dielectric sphere radius "a" and relative permittivity ε_r is placed in a uniform electric field.  The field region is large so the presence of the sphere does not perturb the field sources. 
(a)  Assuming the field inside the sphere to be uniform and the field outside to be described by the uniform field plus a dipole field centered on the sphere, find the fields and the dipole moment induced in the sphere by applying boundary conditions at one point.
(b)  What happens if the sphere is conducting?

Solution:

• Concepts:
  The dipole field, boundary conditions
• Reasoning:
  Place the sphere at the origin.  Assume external field points in the z-direction,
  E_ext = E₀k.
  The external electric field will polarize the sphere.  The electric field of a uniformly polarized sphere is uniform inside the sphere and a pure dipole field outside the sphere.  Assume that the total field inside the sphere is the superposition of the field of a uniformly polarized sphere and the constant external field E₀k.  The superposition of these two fields fulfills all the boundary conditions for D on the surface of the sphere. 
  We have a unique solution as long as inside D = ε_rE inside the sphere.
• Details of the calculation:
  (a)  Let us first concentrate on the field produced by a polarized sphere with dipole moment p.
  The field produced by the polarized sphere outside the sphere is
  E(r) = (4πε₀)^-1(3(p∙r)r/r⁵ - p/r³),
  with p = pk = dipole moment of the sphere.
  Then at r = ak (on the z-axis) we have
  E_out(sphere)= pk/(2πε₀a³) = 2Pk/(3ε₀), with P = p/(4πa³/3).
  E_out(sphere) - E_in(sphere) = (σ_p/ε₀)k = (P/ε₀)k.
  Therefore E_in(sphere) = -Pk/(3ε₀), for the field produced by the polarized sphere.
  Now let us look at the total field inside and outside of the sphere.
  The total field at r = ak (on the z-axis) inside the sphere is E_in = (E₀ - P/(3ε₀))k,  D_in = ε_r(E₀ - P/(3ε₀))k.
  The total field at r = ak (on the z-axis) outside the sphere is
  E_out = (E₀ + 2P/(3ε ₀))k,  D_out = ε₀(E₀ + 2P/(3ε₀))k.
  The normal component of D is continuous.
  ε_r(E₀ - P/(3ε₀)) = ε₀(E₀ + 2P/(3ε₀)),  (2ε₀ + ε_r)P/(3ε₀) = (ε_r - ε₀)E₀.
  P = 3ε₀(ε_r - ε₀)E₀/(2ε₀ + ε_r), p = P4πa³/3 = 4πε₀a³(ε_r - ε₀)E₀/(2ε₀ + ε_r).
  E_in = E₀3ε₀/(2ε₀ + ε_r), D_in = ε_rE_in, p = 4πε₀a³(ε_r - ε₀)E₀/(2ε₀ + ε_r).
  (b)  When the sphere is conducting the total field at r = ak (on the z-axis) inside the sphere is
  E_in = (E₀ - P/(3ε₀))k = 0.
  P = 3ε₀E₀, p = 4πε₀a³E₀.

Problem:

(a)  A spherical dielectric of radius a has a uniform polarization P in the z-direction.
Show that the electric field inside the dielectric due to the polarization is given by E = -P/(3ε₀).
(b)  A large capacitor in vacuum has parallel circular plates of radius R separated by a distance d (d << R).
The capacitor is charged to a potential difference V and disconnected from the source.  Find the energy stored in the capacitor.
(c)  Subsequently, a small sphere of radius a (a << d) and dielectric constant K is placed in the center of the capacitor between the plates.
Find the electric field inside the dielectric.
(d)  Will the capacitor have less, more, or the same energy than before the dielectric was inserted?  Explain!

Solution:

• Concepts:
  Boundary value problems, Φ(r,θ) = ∑_n=0^∞[A_nrⁿ + B_n/rⁿ⁺¹]P_n(cosθ) is the general solution to Laplace's equation for problems with azimuthal symmetry.
• Reasoning:
  ∇²Φ = 0 inside and outside the sphere since ρ_free = 0 inside and outside the sphere.  We are looking for a solution for ∇²Φ = 0, subject to the boundary conditions.
• Details of the calculation:
  (a)  Place the center of the sphere at the origin.
  Then ρ_b = -∇∙P = 0,  σ_b = P ∙ n = P cosθ. 
  We have a sphere with a surface charge density proportional to cosθ.  We solve for the potential and the field using boundary value methods.
  Assume Φ₁ = A₀ + A₁rcosθ  inside,
  Φ₂ = B₀'/r + (B₁'/r²)cosθ  outside.
  We assume all higher-order coefficients are zero.  If we find a solution with this assumption, it is the only solution.
  Boundary conditions:
  (i)  Φ is continuous at r = a.  A₀ = B₀'/a,  A₁a = B₁'/a².
  (ii)  The radial component of D is continuous at r = a.  (There are no free charges.)
  E₁ = -∇Φ₁,  E_1r = -A₁cosθ,  E_1θ = A₁sinθ,  E₁ = -A₁k.
  D₁ = ε₀E₁ + P.
  E₂ = -∇Φ₂.  E_2r = B₀'/r² + 2(B₁'/r³)cosθ,  E_2θ = (B₁'/r³)sinθ,  D₂ = ε₀E₂.
  -ε₀A₁cosθ + P cosθ = ε₀B₀'/a² + 2ε₀(B₁'/a³)cosθ.
  -ε₀A₁ + P = 2ε₀(B₁'/a³),  B₀' = A₀ = 0.
  -ε₀A₁ + P = 2ε₀A₁.  A₁ = P/(3ε₀).
  E₁ = -A₁k = P/(3ε₀).
  
  (b)  U = ½CV²,  C = ε₀A/d = ε₀πR²/d,  U = ½(ε₀πR²/d)V².
  
  (c)  The dielectric sphere is placed in a previously uniform electric field E₀. ( E₀ = V/d)
  The field inside the sphere will be E_in = -∇Φ_in = 3E₀/(K + 2).
  
  (d)  The capacitor is disconnected from the battery.  Q is constant.  The capacitance increases when a dielectric is inserted. 
  The energy stored in the capacitor (U = Q²/2C) is proportional to 1/C for a capacitor with constant Q. 
  The energy stored in the capacitor decreases.

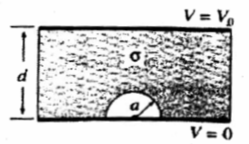
Problem:

Two very large metal plates are held a distance d apart, one at potential zero and the other at potential V₀.  A metal sphere of radius a is sliced in two, and one hemisphere is placed on the grounded plate, so that its potential is likewise zero.  The radius of the sphere a is very small compare to the distance d between the plates, (a << d), so that you may assume that the electric field near the upper plate is constant.  If the region between the plates is filled with a weakly conducting material of conductivity σ, what current flows to the hemisphere?

Solution:

• Concepts:
  Boundary value problems, azimuthal symmetry.
• Reasoning:
  Put the origin of the coordinate system at the center of the sphere. Then
  Φ(r,θ) = ∑_n=0^∞[A_nrⁿ + B_n/rⁿ⁺¹]P_n(cosθ)
  is the most general solution in the region between the plates, since the charge density ρ = 0 there.  To find the specific solution we apply boundary conditions.
• Details of the calculation:
  The boundary conditions are Φ = 0 on the lower plate and the sphere and Φ = V₀ on the upper plate.
  Φ = A₁'rcosθ  + (B₁'/r²)cosθ  between the plates.
  We assume all other coefficients are zero.  If we find a solution with this assumption, then the uniqueness theorem guaranties that it is the only solution.
  Boundary conditions:
  (i)  Φ is continuous at r = a.  0 = A₁'a + B₁'/a².  B₁' = -A₁'a³.
  (ii)  E = -∇Φ = -E₀k at r >> a,  i.e. far away from the hemispherical boss.
  -A₁'cosθ = -E₀cosθ,  A₁'sinθ = E₀sinθ,  A₁' = E₀,  B₁' = -E₀a³.
  Φ(z = d) = V.  E₀d = V,  E₀ = V/d
  Φ = E₀rcosθ  - (E₀a³/r²)cosθ.

  E = -∇Φ.  E_r = -E₀cosθ  - 2(E₀a³/r³)cosθ,  E_θ = E₀sinθ - (E₀a³/r³)sinθ.
  E = constant field + field due to polarized sphere.
  At the surface of the sphere at r = a, E is perpendicular to the surface and therefore radial.
  E_r(a) = -3E₀cosθ. 
  
  j = σE is the current density between the plate.
  The current flowing to the hemisphere is
  ∫₀^{π /2}j(θ)2πa² sinθ dθ = 6πσE₀a² ∫₀^{π /2}cosθ sinθ dθ = 3πσ E₀a² = 3πσ Va²/d = I.

Cylindical coordinates:  Φ = Φ(ρ,φ)  (0 ≤ φ  ≤ 2π) independent of z

Problem:

A long cylindrical rod of radius a and dielectric constant k is placed in a uniform electric field E₀ with its axis perpendicular to the field direction.
(a)  Find the potential Φ inside and outside the rod.
(b)  Find the electric field E inside and outside the rod.
(c)  Find the volume and surface polarization charge density.

Solution:

• Concepts:
  Boundary value problems, 
  Φ(ρ,φ) = ∑_n=1^∞(A_ncos(nφ) +  B_nsin(nφ))ρⁿ + ∑_n=1^∞(A'_ncos(nφ) +  B'_nsin(nφ))ρ^-n +a₀ + b₀lnρ
  is the general solution to Laplace's equation if Φ = Φ(ρ,φ)  (0 ≤ φ  ≤ 2π) in cylindrical coordinates.
• Reasoning:
  Φ = Φ(ρ,φ)  (0 ≤ φ  ≤ 2π) independent of z.  The problem involves the whole azimuthal range.
• Details of the calculation:
  (a)  Let E = Ei.  Assume that all B_n and B_n' and all A_n and A_n' with n > 1 are zero in the general solution.  If we find such a solution that satisfies all boundary conditions, then it is a unique solution.
  Boundary conditions:
  ρ < a:  Φ is finite at the origin.  Choose Φ(0) = 0.  Then Φ(ρ,φ) = A_1icos(φ)ρ.
  ρ > a:  -∇Φ = Ei as ρ --> infinity.  Φ(ρ,φ) = A_1ocos(φ)ρ + A_1o'cos(φ)/ρ,  A_1o = -E.
  ρ = a:  Φ is continuous,   D∙n is continuous.
  A_1icos(φ)a = -Ecos(φ)a + A_1o'cos(φ)/a,  A_1i + E =  A_1o'/a².
  εA_1icos(φ) = -ε₀Ecos(φ) - ε₀A_1o'cos(φ)/a²,  (ε/ε₀)A_1i + E =  -A_1o'/a².
  Algebra:  A_1i = -E(2ε₀/(ε + ε₀)), A_1o' = a²E[(ε - ε₀)/(ε + ε₀)]
  Φ_inside = -E(2ε₀/(ε + ε₀))cos(φ)ρ,  Φ_outside = -Ecos(φ)ρ + a²E[(ε - ε₀)/(ε + ε₀)]cos(φ)/ρ.
  
  (b)  E = -∇Φ.  E_ρ = ∂Φ/∂ρ,  E_φ = (1/ρ)∂Φ/∂φ.
  E_in = E(2ε₀/(ε + ε₀))(cos(φ)[ρ/ρ] - sin(φ)[φ/φ]) = (2ε₀/(ε + ε₀))Ei.
  E_out = Ei + E(a²/ρ²)[(ε - ε₀)/(ε + ε₀)](cos(φ)[ρ/ρ] + sin(φ)[φ/φ]).
  
  (c)  ∇∙P = -ρ_bound = -ε₀x_e∇∙E = 0 since E = constant inside the rod.
  P∙n = σ_bound = ε₀x_eE_in∙[ρ/ρ] = (ε + ε₀)E_in∙[ρ/ρ] = (2ε₀(ε - ε₀)/(ε + ε₀))Ecos(φ).