Capacitors with dielectrics

Parallel plate capacitors

Problem:

Regarding the Earth and a cloud layer 800 m above the Earth as the plates of a capacitor, calculate the capacitance if the cloud layer has an area of (1 km)².  If an electric field of 3*10⁶ N/C makes the air break down and conduct electricity, (that is, cause lightning,) what is the maximum charge (in C) the cloud can hold?

Solution:

• Concepts:
  Capacitor with dielectric
• Reasoning:
  For air, ε = ε₀ to a good approximation.  For a parallel plate capacitor C = ε₀A/d.
• Details of the calculation:
  A = 1 km² * (1000m/km)², d = 800 m,  E_max = 3*10⁶ N/C.
  V_max  = E_maxd,  Q_max = CV_max = CE_maxd  = ε₀AE_max = 8.85*10^-12 C/(V m) * 10⁶ m² *  3*10⁶ N/C,
  Q_max = 26.6 C.

Problem:

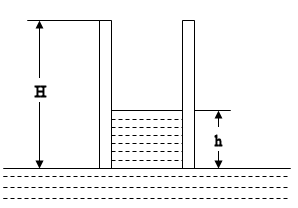
A plane capacitor with rectangular plates (height H times width l) is fixed in a vertical position.  The distance d between the plates is much smaller than the linear dimensions of the plates.  The capacitor is charged and disconnected from the battery.  The initial magnitude of the electric field between the plates is E₀.  The lower part of the capacitor is now brought into contact with a dielectric liquid of density ρ and relative electric permittivity κ_e.  Determine the height h of the liquid between the plates and explain the phenomenon.  Neglect capillarity effects.

Solution:

• Concepts:
  Capacitor with dielectric, energy conservation
• Reasoning:
  When the plates contact the liquid's surface, a force in the upward direction is exerted on the dielectric liquid.  The total charge on each plate remains constant and there is no energy transferred to the system from outside.  The increase of the gravitational energy of the liquid is equal in magnitude to the decrease of the energy stored in the capacitor.
• Details of the calculation:
  The initial energy on the capacitor is
  W₀ = ½C₀V₀² = ½Q₀²/C₀ where C₀ = ε₀Hl/d.
  Let W₀ = the total potential energy, W₁ = the energy stored in the capacitor and W₂ = the gravitational potential energy.

  W₀ = W₁ + W₂,  W₁ = ½Q₀²/C,  W₂ = ½ρgh²ld.
  C = C₁ + C₂ = ε₀κ_ehl/d + ε₀(H - h)l/d .
  Inserting the expressions for C₀ and C, and substituting E₀C₀d = Q₀ we find
  (κ_e - 1)h² + Hh - E₀²ε₀H(κ_e - 1)/(ρg) = 0

  Solving for h we obtain h = ½H/((κ_e - 1) ± (½H/(κ_e - 1))[1 + 4E₀²ε₀(κ_e - 1)²/(ρgH)]^½.
  Only the positive solution makes sense.  Taking in account that H is much larger than h we obtain the final result
  h ≈ E₀²ε₀(κ_e - 1)/(ρg).

Problem:

A rectangular block of dielectric material with permittivity ε is partially inserted between two parallel plane conducting plates.  The plates are square, of side l, and are separated by a distance d, with d << l.  The dielectric is also square, of side l, and has a thickness of almost d.  A potential V is applied across the plates.  When the dielectric has a length x inserted between the plates, calculate the force on the dielectric, including its direction.

Solution

• Concepts:
  Capacitance, energy conservation
• Reasoning:
  We find the work done by external agents as a dielectric is inserted into a capacitor and the capacitance changes.
• Details of the calculation:
  Capacitance as a function of x:  C = εlx/d + ε₀l(l -x)/d,
  Total energy store in the capacitor:  U = ½CV².
  dW_mech + dW_bat = dU.  dW_bat = dQV = dCV².  dU = ½dCV². 
  dW_mech = -½dCV². 
  F_x = -dW_mech/dx = ½V²dC/dx = ½V²(ε -  ε₀)l/d.
  The dielectric is pulled towards the right, into the capacitor.

Problem:

A parallel-plate capacitor is connected to a battery which maintains a potential difference V₀ between its plates.  A slab of dielectric constant K is inserted between the plates, completely filling the space between them.
(a)  Show that the battery does an amount of work q₀V₀(K - 1) during the insertion process, if q₀ is the charge on the capacitor plates before the slab is inserted.
(b)  How much work is done by mechanical forces on the slab when it is inserted between the plates?  Is this work done on, or by, the agent inserting the slab?

Solution:

• Concepts:
  Capacitance, energy conservation
• Reasoning:
  We must find the work done by external agents as a dielectric is inserted into a capacitor and the capacitance changes.
• Details of the calculation:
  (a)  before insertion:  Q₀ = C₀V₀,  C₀ = ε₀A/d.
  after insertion: Q = CV₀,  C = εA/d.  Q > Q₀.
  Work done by the battery: 
  W_bat = (Q - Q₀)V₀  = (C - C₀)V₀² = (ε - ε₀)V₀²A/d = (Aε₀/d )(K - 1)V₀² = Q₀V₀(K - 1).
  The battery does positive work.
  (b)  Total energy stored in the capacitor before insertion:  U₀ = ½C₀V₀².
  Total energy stored in the capacitor after insertion:  U = ½CV₀².
  ΔU = U - U₀ = ½V₀²(C - C₀) = ½Q₀V₀(K - 1).
  Only ½ of the work done by the battery is stored as electrostatic potential energy.
  W_mech + W_bat = ΔU,  W_mech = ΔU - W_bat = -½Q₀V₀(K-1).
  The agent inserting the slab does negative work, the electric field does positive work inserting the slab, the slab is being pulled in and, if no other forces are acting on it, gains kinetic energy.

Problem:

(a)  A container is made of two square metal plates of side w held a distance of d apart by insulator ends and bottom.  Assume that the end and bottom insulator pieces have a dielectric constant of 1.  The two metal sides of the container form a capacitor and are attached to a battery of potential difference V.  Find the total energy stored in the electric field when container is empty.  You may assume that d << w.
(b)  A dielectric liquid of dielectric constant k is poured into the box until it is half full.  What will then be the total energy in the capacitor?
(c)  Calculate the amount of energy given up by the source during the dielectric-filling operation in part (b).
(d)  If the dielectric has a density ρ and is poured from a height w above the top of the container, with what velocity will the first droplets of dielectric strike the bottom of the container?

Solution:

• Concepts:
  Capacitor with dielectric, energy conservation
• Reasoning:
  We are asked to find the energy stored in a capacitor partially filled with a dielectric.
• Details of the calculation:
  
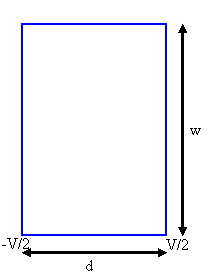
  (a)  U = ½CV²,  C = e₀w²/d,  U = ½(ε₀w²/d)V².
  (b)  U' = ½C'V²,  C' = C₁ + C₂,  C₁ = ε₀w²/(2d),  C₂ = kε₀w²/(2d),  U = ½(1+k)(ε₀w²/(2d))V².
  (c)  Before filling:  Q = CV,  after filling:  Q' = C'V.
  Work done by source:  (Q' - Q)V = (C' - C)V² = (1-k)(ε₀w²/(2d))V².
  (d)  Assume the container contains dielectric up to a height h.  The energy stored in the capacitor is
  U' = ½C'V²,  C' = C₁ + C₂ = kε₀hw/d + ε₀(w-h)w/d.
  Now add a drop of dielectric, so that the height increases from h to h + δh.
  The energy stored in the capacitor now is
  U'' = ½C''V²,  C'' = kε₀(h + δh)w/d + ε₀(w - h - δh)w/d.
  ΔU = U''-U' = ½(C'' - C')V² = ½V²(k-1)(ε₀ δh w/d).
  The work done by the battery is (C'' - C')V² = 2ΔU.
  Therefore the kinetic energy of the drop increases by an amount ΔU over what it would be from just free-falling.
  T = T₁ + T₂,  T₁ = mg2w,  T₂ = ΔU.
  ½mv² = mg2w + ΔU.  v² = 4gw + 2ΔU/m.
  m = ρ d w δh,  v² = 4gw + (k-1)ε₀V²/(ρd²).

Problem:

Two parallel vertical metal plates, shaped as squares with side h, are held above the surface of a non-conducting liquid of density ρ so that their bottom edges touch the surface of the liquid.  The plates are a distance d apart.  After the plates are connected to a battery that maintains a constant voltage V, the liquid rises between the plates, barely reaching their top edges.  Neglecting the effects of surface tension, find the dielectric constant k of the liquid.

Solution:

• Concepts:
  Capacitance, energy conservation
• Reasoning:
  We must find the work done by external agents as a dielectric is inserted into a capacitor and the capacitance changes.
• Details of the calculation:
  When the capacitor is connected to the battery, the energy stored in the air-filled capacitor is U = ½ CV², and the charge on each plate is q = CV.  When the capacitor is filled with the dielectric liquid, its capacitance becomes kC, where k is the dielectric constant of the liquid.  This increases the charge stored on each plate to kCV.  The additional charge of (k - 1)CV came through the battery, which did some work, given by ΔqV = (k - 1)CV².  However, the electrical energy stored in the capacitor only increases by ½kCV² - ½CV² = ½(k - 1)CV².  The other half of the work done by the battery goes into raising the liquid into the capacitor.
  An amount of liquid of volume h²d and mass ρh²d is raised into the capacitor.  The center of mass of the liquid is raised to the midpoint of the capacitor, a distance of h/2.  So the increase in the gravitational potential energy of the liquid is mgΔy = ρh³dg/2.  The work done by the battery is equal to the change in energy of the system, namely the increase in the capacitor's stored electrical energy and the increase in the gravitational potential energy of the liquid.
  (k - 1 )CV² = ½(k-1)CV² + ½ρgdh³.
  k = 1 + ρgdh³/(CV²).
  C = ε₀h²/d for a parallel plate capacitor.
  k = 1 + ρgd²h/(ε₀V²).

Cylindrical capacitors

Problem:

A cylindrical capacitor of length L, with an inner radius a and outer radius b, is filled with a solid dielectric (permittivity ε).  If we can ignore the top/bottom end effects,
(a)  find the electric field for a < r < b when the charge on the capacitor is Q;
(b)  find the capacitance.
(c)  A potential difference V is maintained between the two cylinders. The solid dielectric is displaced down by a distance x < L.  Find the total capacitance now, and
(d)  find the magnitude and direction of the force acting on the solid dielectric.

Solution:

• Concepts:
  Gauss' law, relationship between E, and D, capacitance, U = ½CV²
• Reasoning:
  The problem has cylindrical symmetry.
• Details of the calculation:
  (a)  For a given charge on the cylinder we find D from Gauss' law for D.  We then use D to find E, V, and C.
  D = (λ_f/2πr)(r/r) (a < r < a) from Gauss' law for D.  Here r is a cylindrical coordinate and we use SI units.
  E = (λ_f/2πεr)(r/r) = (Q/2Lπεr)(r/r)
  (b)  ΔV = ∫_a^bEdr = ∫_a^b(D/ε)dr = (Q/(2Lπε)ln(b/a).
  C = Q/ΔV = (2Lπε)/ln(b/a).
  (c)  Capacitors in parallel:  C' = (2(L - x)πε)/ln(b/a) + (2xπε₀)/ln(b/a).
  (d)  The energy stored in the capacitor is U = ½CV². 
  With the dielectric partially removed the capacitance is
  C' = (2(L - x)πε)/ln(b/a) + (2xπε₀)/ln(b/a) < C.
  The energy stored in the capacitor decreases by ΔU = ½( C' - C)V².
  The charge on the capacitor is Q = CV.
  When the dielectric is partially removed, ΔQ = (C' - C)V is removed from the cylinders.
  An amount of (negative) work W = ΔQ V = (C' - C)V² is done by the battery.
  The energy stored in the capacitor decreases only by ½( C' - C)V².  The mechanical work done must therefore equal W = ½(C - C')V².  W is positive, an external force has to pull the dielectric out of the capacitor.
  The electrostatics force acting on the dielectric is F = -dW/dx = ½V²(dC'/dx) = V²π(ε₀ - ε)/ln(b/a).
  The dielectric is pulled into the capacitor by the electrostatic force.