Gauss' law for D
Gauss' law, spherical symmetry
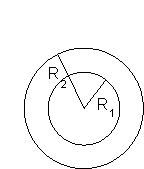
Problem:
A spherical capacitor with conducting surfaces of radii R1
and R2 has a material of dielectric constant
ε(r) = ε0(R1/r)2
between the spheres.
(a) Find the capacitance C of the capacitor.
(b) If the charge on the capacitor is Q find the total energy stored in
the capacitor.
Solution:
- Concepts:
Gauss' law for D.
- Reasoning:
The problem has spherical symmetry. We can find the field between the
surfaces in terms of the charge Qfree on the surfaces using
Gauss' law for D.
- Details of the calculation:
(a) Symmetry:
D = D (r/r),
E = E (r/r).
if the origin is located at the center of the spheres.
Gauss' law for D: D4πr2 = Qfree
inside in SI units.Free charges reside only on the surfaces of the
capacitor. Between the surfaces we have
D = Qfree/( 4πr2),
D(r) = ε(r)E(r),
V = ∫R1R2 E(r)dr = ∫R1R2 dr D(r)/ε(r)
= ∫R1R2 dr Qfree/(4πε0R12).
V = Qfree(R2 - R1)/(4πε0R12).
C = Qfree/V = 4πε0R12/(R2 - R1)
is the capacitance of the capacitor.
(b) U = ½Q2/C = Q2(R2
- R1)/(8πε0R12)
is the total energy stored in the capacitor.
Problem:
A spherical conductor of radius a is surrounded with a
dielectric shell of outer radius b. The dielectric constant
varies with radius as K = 1 + n(r - a), where n is a constant. A charge
Q is placed on the conductor.
(a) Find the electric displacement and the electric field at all
points in space.
(b) Find the distribution of bound charges in the interior of and
on the surface of the dielectric shell.
(c) Find the total energy stored in the system.
Solution:
Problem:
A linear dielectric sphere
of radius a and dielectric constant
ke carries a uniform
charge density ρ,
surrounded by vacuum.
(a) Find E and
D inside and outside the
sphere.
(b) Find the energy U of the system.
Solution:
- Concepts:
Gauss' law, relationship between E, and
D,
energy in dielectrics
- Reasoning:
We find D from Gauss' law for D. We then use
D to
find E and U.
- Details of the calculation:
(a) E and D are radial.
r < a: D(r)4πr2
= 4πr3ρ/3,
D(r) = rρ/3. E(r) = D(r)/(ε0ke)
= ρr/(3ε0ke)
= Qtotr/(4πε0kea3)
r > a: D(r)4πr2
= 4πa3ρ/3, D(r) = a3ρ/(3r2) = Qtot/(4πr2).
E(r) = a3ρ/(3ε0r2)
= Qtot/(4πε0r2).
(b) The energy U of the system is U = ∫all
space(ε/2)E2dV.
U = 2πε∫0aE2r2dr
+ 2πε0∫a∞E2r2dr
= [Qtot2/(8πε0)][1/(5ake)
+ 1/a]
= [2ρ2π/(9ε0)][a5/(5ke)
+ a5].
Gauss' law, cylindrical symmetry
Problem:
A
capacitor is made of two concentric cylinders of radii r1
and r2 (r1 < r2) and
length L >> r2.
The region between r1
and r3 = (r1r2)½ is filled with a circular
cylinder of length L and dielectric constant k.
The
remaining volume is an air gap.
(a) What is the capacitance?
(b) What are the values of E, P, and D at a radius r
inside the dielectric (r1 < r < r3)?
Assume a potential difference V between r1 and
r2.
(c) How much mechanical work must be done to remove the dielectric
cylinder while maintaining this constant potential difference between r1
and r2?

Solution:
- Concepts:
Gauss' law, relationship between E,
P, and
D,
capacitance, U = ½CV2.
- Reasoning:
For a given charge on the cylinder we find D from Gauss' law for
D.
We then use D to find E,
P, V, and C.
- Details of the calculation:
(a) D = (λf/(2πr)) (r/r)
(r1 < r < r2) from Gauss' law for
D.
Here r is a cylindrical coordinate and we use SI units.
ΔV = ∫r1r2 E(r)dr = ∫r1r3
dr D(r)/(ε0k) = ∫r1r2 dr D(r)/ε0
= (λf/(2πε0k))[ln(r3/r1)
+ k ln(r2/r3)]
= (λf/(2πε0k))[ln√(r2/r1)
+ k ln(√r2/r3)]
= (λf(1 + k)/(2πε0k))ln√(r2/r1).
C = Qf/ΔV
= λfL/ΔV
= [4πε0kL/(k + 1)][1/ln(r2/r1)].
(b)
D = (λf/(2πr))(r/r),
E = (λf/(2πε0kr)) (r/r),
P = ε0χeE
= ε0(k - 1)E = (λf/(2πr))[(k - 1)/k] (r/r).
We can write this in terms of ΔV using the result
of part (a).
(c) The energy stored in the the capacitor is U = ½CV2.
Without the dielectric the capacitance is Cout = 2πε0L/ln(r2/r1)
< C.
The energy stored in the capacitor decreases by
ΔU
= ½(Cout - C)V2.
The charge on the capacitor is Q = CV.
When the dielectric is removed,
ΔQ = (Cout
- C)V is removed from the cylinders.
An amount of (negative) work W =
ΔQ V = (Cout
- C)V2 is done by the battery.
The energy stored in the capacitor decreases only by ½(Cout -
C)V2.
The mechanical work done must therefore equal W =
½(C - Cout)V2.
W = [2πε0L/ln(r2/r1)]V2(k - 1)/(k + 1).
Problem:
A 500 m length of high-voltage cable is undergoing electrical testing. The
cable consists of two coaxial conductors, the inner of 5 mm diameter and the
outer of 9 mm internal diameter. The space between the conductors is filled
with polythene which has a relative permittivity of 2 and which can withstand
electric field strength of 60 MVm-1.
(a) Find the maximum voltage which can be applied between the conductors and
the energy stored in the cable at this voltage.
(b) If the cable is to be discharged to a safe level of 50 V in 1 minute, what
value of resistance must be connected across it? What is the maximum power and
the total energy dissipated in the resistance?
Solution:
- Concepts:
Gauss' law, the cylindrical capacitor
- Reasoning:
The problem has enough symmetry to find
D(r) and E(r) from Gauss'
law alone.
- Details of the calculation:
(a) From Gauss' law: D(r), E(r ) ∝ 1/r between the cylinders.
Let the outer cylinder be grounded and V0 be positive. Then the
direction of E is radially outward.
E(r) = A/r, with A positive. Then V0 = -∫b/2a/2E(r)dr
= A∫a/2b/2(1/r)dr
= A(lnb/2 - lna/2) = Aln(b/a). A = V0/ln(b/a),
with a = 5 mm and b = 9 mm.
E(r) = V0/(r ln(b/a)).
If Emax = E(a/2) = 2V0/(a ln(b/a)) = 60 MV/m, then
V0 = (6*107 V/m)*(2.5*10-3 m)*ln(9/5) = 8.82*104
V is the maximum voltage which can be applied.
Energy stored in the cable:
W = (ε/2)∫E2dV = (εL/2)2π∫a/2b/2E2rdr
= επL∫a/2b/2(V0/(rln(b/a)))2rdr.
W = [επLV02/ln(b/a)] = [2πε0(500 m)*(8.82*104
V)2/ln(9/5)] = 368 J.
(b) The cable is a capacitor. W= U = ½CV2, C =
2επL/ln(b/a).
Discharging the cable through a resistor R amounts to amounts to discharging
a RC circuit wit time constant τ = RC. If the voltage decreases from V1
to V2 , the energy stored in the capacitor decreases by an amount
ΔU = ½C(V22 - V12).
V = V1exp(-t/τ). V2/V1 = exp(-t'/τ)
where t' is time it takes to reach V2.
ln(V1/V2) = t'/τ.
The power dissipated in the resistor is P = V2/R = (V12/R)exp(-2t/τ).
The total energy dissipated is Ediss = (V12/R)∫0t'exp(-2t/τ)dt
= (V12τ/(2R))(1 - exp(-2t'/τ)).
Ediss = ½V12C(1 - exp(-2ln(V1/V2)))
= ½V12C(1 - (V2/V1)2)
= ½C(V12 - V22) ~ 368 J.
Ediss + ΔU = 0.
Gauss' law, planar symmetry
Problem:
The dielectric of a parallel plate capacitor
has a permittivity that varies as ε1 + ax,
where x is the distance from one plate. The area of each plate is A
and their spacing is s.
Assume a surface charge density ±σfree
for the plates.
(a) Find the capacitance.
(b) Assume ε1 + ax varies from
ε1 to 2ε1. Find P from
D and E for that case.
(c) Find the polarization charge density ρp.
Solution:
- Concepts:
Gauss' law, relationship between E,
P, and
D
- Reasoning:
Assuming a surface charge density, Gauss' law for D can be used to find D,
then E, then V. We then can find C = Q/V.
- Details of the calculation:
(a)
Gauss' law for D yields DΔA = σfreeΔA, D = σfree, D =
εE.
V = ∫0sEdx =
∫0sdx/(ε1
+ ax) = (σfree/a)ln(1 + as/ε1)).
C = Q/V = σfreeA/((σfree/a)ln(1 + as/ε1))
= aA/ln(1 + as/ε1).
If a << ε1 then ln(1 + as/ε1)
≈ as/ε1 -
½(as/ε1)2 + ... .
C ≈ ε1A/s.
(b) 2ε1 =
ε1 + as. a = ε1/s.
ε = ε1
+ (ε1/s)x.
D = σfreei,
E
= σfreei/(ε1
+ (ε1/s)x), P =
D -
ε0E = σfreei(1
- [ε0/(ε1
+ (ε1/s)x)]
(c) ρp =
-∇∙P = -∂P/∂x
= -σfreeε0(ε1/s)/(ε1
+ (ε1/s)x)2 = -σfrees(ε0/ε1)/(s
+ x)2.
σp = P∙n.
At x = 0 σp = -σfree(1 - ε0/ε1).
At x = s σp = σfree(1 - ε0/2ε1).
Problem:
The plates of an isolated parallel-plate capacitor have area A and are
separated by a distance d << A½. Let one plate be located in the y-z
plane at x = 0 and the other plate at x = d. The plate at x = 0 carries a
charge +Q and the plate at x = d carries a charge -Q. Dielectric 1 with
permittivity ε = ε0 + ax fills the region between the plates from x =
0 to x = d/2, and dielectric 2 with permittivity ε = ε0 + a(d - x) fills
the region between the plates from x = d/2 to x = d. Let a = ε0/d.
(a) Find the electric displacement and the electric field between the
plates.
(b) Find the voltage across the plates.
(c) Find the distribution of bound charges in the interior of and on the
surfaces of both dielectrics.
Solution:
- Concepts:
Gauss' law for D
- Reasoning:
Gauss' law can be used to find D. Given
D, we find
E,
P, V, and the charge densities.
- Details of the calculation:
(a) Gauss' law for D:
D = σ i = (Q/A)i. E
= D/ε.
E = σ i /(ε0 + ax), 0 < x < d/2,
E = σ i
/(ε0 + a(d - x)), d/2 < x < d.
(b) V = σ∫0d/2dx (1/(ε0 + ax)) +
σ∫d/2ddx
(1/(ε0 + a(d - x)))
= (σ/a)∫ε0 ε0 +ad/2dx' (1/x') - (σ/a)∫ ε0+ad/2
ε0 dx' (1/x')
= 2(σd/ε0)ln(1 + ½).
V = 2(σd/ε0)ln(3/2).
(c) P = (ε - ε0)E.
P = (ε0x/d)E,
0 < x < d/2, P = (ε0(d - x)/d)E, d/2 < x < d.
P = (xσ/(d + x))i, 0 < x < d/2,
P = (σ(d-x)/(2d - x))i,
d/2 < x < d.
ρp = -∇∙P = -σd/(d + x)2, 0 < x < d/2, is the
volume charge density in dielectric 1.
ρp = -∇∙P = σd/(2d - x)2, d/2 < x < d, is the
volume charge density in dielectric 2.
σp = P∙n is the expression for the surface charge
density of bound charges.
σp = 0 on the surfaces of the dielectrics at x = 0 and x = d.
σp = σ/3 on the surface of dielectric 1 at x = d/2.
σp = -σ/3 on the surface of dielectric 2 at x = d/2.


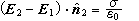 (SI
units).
(SI
units).