The method of images with dielectrics

Problem:

A charge q is situated at the point x = h > 0, y = z = 0 outside a homogeneous dielectric which fills the region x < 0.
(a)  Write the electric fields just outside and just inside the dielectric in terms of the charge q and surface charge density σ_b of bound charges on the surface of the dielectric.
(b)  Express σ_b in terms of the electric field just inside the dielectric.  Let K be the dielectric constant of the dielectric.
(c)  By using the equations obtained in (a) and (b), show that
σ_b = -[1/(2π)][(K - 1)/(K + 1)][qh/(h² + y² + z²)^3/2].
(d)  Calculate the electric field E' due to σ_b at the position (h,0,0) of the charge q.  Show that it can be interpreted as the field of an image charge q' situated at the point (-h,0,0).
(e) Show that the charge q experiences the force F = -[(K - 1)/(K + 1)] (q²/4h²)i.

Solution:

• Concepts:
  Polarization, polarization charge densities
• Reasoning:
  The field of the point charge polarizes the dielectric and induces a  surface polarization charge density, σ_b = P∙n.
• Details of the calculation:
  (a)  The field due to a surface charge density σ is σ/(2ε₀) n just outside the surface.
  Therefore E_out(0,y,z) = 2πkσ_b(y,z) i + kq/(h² + y² + z²)^3/2 [-hi + yj + zk].
  Here k = 1/(4πε₀).
  Just inside the surface E_in(0,y,z) = -2πkσ_b(y,z) i + kq/(h² + y² + z²)^3/2 [-hi + yj + zk].
  
  (b) P = ε₀(K - 1)]E_in,  σ_b = P∙n = ε₀(K - 1)E_{x_in}(0,y,z)
  
  (c)  σ_b = -ε₀(K - 1)[2πkσ_b + kqh/(h² + y² + z²)^3/2].
  σ_b + ε₀(K - 1)2πkσ_b = -ε₀(K - 1)kqh/(h² + y² + z²)^3/2.
  σ_b = -[1/(2π)][(K - 1)/(K + 1)][qh/(h² + y² + z²)^3/2].
  
  (d)  E'(h,0,0) = ik∫hσ_bdA/(h² + y² + z²)^3/2
  is the field due to σ_b at the position of q.  The components perpendicular to i cancel.
  E'(h,0,0) = -ik[q/(2π)][(K - 1)/(K + 1)]h²∫₀^2πdφ∫₀^∞ρdρ/(h² + ρ²)³
  E'(h,0,0) = -ikq[1/(2π)][(K - 1)/(K + 1)]*(π/2) = -ikq[(K - 1)/(K + 1)]/(4h²).
  This is the same field as that of a point charge q' = -q(K - 1)/(K + 1) located at (-h, 0, 0).
  
  (e) F = qE' = -i kq²[(K - 1)/(K + 1)]/(4h²).

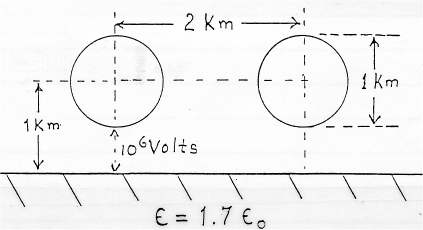
Problem:

Two spherical clouds, each of 1 km diameter, are separated by a distance of 2 km (center-to-center).  Each cloud is uniformly charged with charge density ρ₀.  They are floating with their centers 1 km above a fresh-water mountain lake of non-conducting pure water with dielectric constant ε = 1.7ε₀.  The bottom surface of each cloud is at a potential of 10⁶ volts compared to the lake immediately below it.
(a)  What is the charge density ρ₀?
(b)  What is the electrostatic force on each cloud?
(c)  What is the index of refraction of the lake water?

Solution:

• Concepts:
  The method of images, Coulomb's law
• Reasoning:
  The electrostatic force on each cloud is the same as that due to the charges on the other cloud and due to the images charges behind the dielectric-dielectric interface.
• Details of the calculation:
  
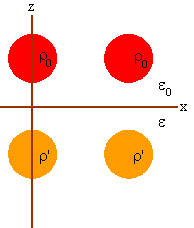
  (a)  Pick a coordinate system:
  Center of cloud 1: r₁ = (0, 0,1 )
  Center of cloud 2: r₂ = (2, 0, 1)
  The potential in the region z > 0 can be found by postulating two image charges.
  Center of image cloud 1: r₁' = (0, 0, -1)
  Center of image cloud 2: r₂' = (2, 0, -1)
  The charge density of each image cloud is
  ρ' = -ρ₀(ε - ε₀)/(ε + ε₀) = -(0.7/2.7)ρ₀  = -0.26ρ₀.
  Find the potential at r = (0, 0, 0):
  Φ(r) = [ρ₀(4/3)π(0.5 km)³/(4πε₀)][1/(1 km) - 0.26/(1 km) + 1/(5^½ km) - 0.26/(5^½ km)]
  = 4.47*10⁴(ρ₀/ε₀)m².
  Find the potential at r = (0, 0, 0.5):
  Φ(r) = [ρ₀(4/3)π(0.5 km)³/(4πε₀)][1/(0.5 km) - 0.26/(1.5 km) + 1/((4.25)^½ km) - 0.26/((6.25)^½ km)]
  = 9.20*10⁴(ρ₀/ε₀)m².
  ΔΦ = 10⁶ V = (9.20 - 4.47)10⁴(ρ₀/ε₀)m²,  ρ₀ = 1.87*10^-10 C/m³.
  (b)  Take cloud 1.  The force on cloud 1 is the same as that due to cloud 2 and image clouds 1 and 2.
  The force on cloud 1 due to each of these clouds is the same as that due to point charges with the same total charge at the center of the clouds.  It can be calculated assuming the total charge of cloud 1 is at its center.
  Force on cloud 1: 
  F_x = [ρ₀V/(4πε₀)][ρ₀V/(4 km²) + (2/8^½)ρ'V/(8 km²)]
  F_z = [ρ₀V/(4πε₀)][ρ'V/(4 km²) + (2/8^½)ρ₀V/(8 km²)]
  Here V = (4/3)π(0.5 km)³.
  F = F_xi + F_zk
  Force on cloud 2: 
  F = -F_xi + F_zk  from symmetry.
  (c)  n = c/v = (εμ/ε₀μ₀)^½.  Assume μ = μ₀, then n = (ε/ε₀)^½ = (1.7)^½ = 1.3.