Problem:

Show that the magnitude of the magnetic field B at the center of a loop of wire carrying a current I and shaped like a regular plane polygon of 2n sides, the distance between parallel sides being 2a, is 
[nμ₀I/(πa)]sin(π/2n),
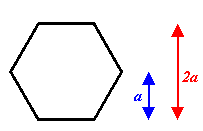
using the Biot-Savart law.  The n = 3 case is shown.

Solution:

• Concepts:
  The Biot-Savart law, the principle of superposition
• Reasoning:
  We find the field of a single segment using the Biot-Savart law.  The principle of superposition then lets us add the fields of the different segments.
• Details of the calculation:
  
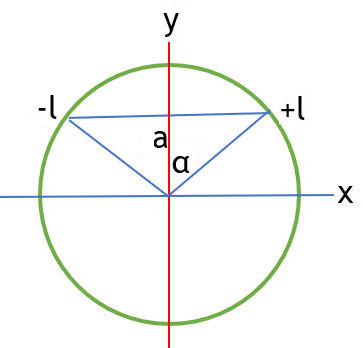
  The field B at the center of the circle due to the current in the wire from -l to +l is
  B(r) = (μ₀/(4π))∫_vI dl' × (r-r')/|r-r'|³.   (SI units).
  Here r = 0,  r' = xi + aj,  dl' = dxi, |r-r'| = (x² + a²)^½.
  dl' x (r-r') = -(a dx) k
  B(0) = -(μ₀Ia/(4π))∫_-l^l dx/(x² + a²)^3/2
  = -[μ₀I/(4πa)]2l/(l² + a²)^½ k = -[μ₀I/(2πa)]sin(α) k.
  For a regular plane polygon of 2n sides we have 2n wire segments. For each segment 2a = 2π/(2n), a = π/(2n).
  Symmetry dictates that B(0) due to each segment is the same.
  B(0) = -[2nμ₀I/(2πa)]sin(π/2n) k = -[nμ₀I/(πa)]sin(π/2n).

Problem:

A large number, N, of closely spaced turns of fine wire are wound in a single layer upon the surface of a wooden sphere of radius R, with the planes of the turns perpendicular to the axis of the sphere and completely covering its surface.  If the current in the windings is I, determine the magnetic field at the center of the sphere.

Solution:

• Concepts:
  The Biot-Savart law, the principle of superposition
• Reasoning:
  A steady current is flowing in a circular loop and we are asked to find the magnetic field on the axis of this loop.
• Details of the calculation:
  (a) Let the axis of the sphere be the z-axis.
  Consider a ring at θ with width dθ.  From the Biot-Savart law we have
  dB(r) = (μ₀/(4π))[I dl x (r-r')/|r-r'|³].  This yields the field at the origin due to the ring.
  dB(r) = (μ₀/2)IR²sin²θ/R³ (z/z).
  In terms of a surface current density k we have I = kRdθ and dB = (μ₀/2)ksin²θdθ (z/z).
  The field due to all loops is 
  B = ∫ dB = (z/z) (μ₀k/2)∫₀^πsin²θdθ = (z/z) (μ₀kπ/4).
  We have Nd = πR, d = diameter of the wire, k = I/d = IN/(πR).
  Therefore the field at the origin is B = (μ₀IN/(4R)) (z/z).

Problem:

What current is required in the windings of a long solenoid that has 1000 turns uniformly distributed over a length of 0.4 m in order to produce at the center of the solenoid a magnetic field of 10^-4T?

Solution:

• Concepts:
  The magnetic field inside a solenoid
• Reasoning:
  We are asked to find the magnetic field in the center of a solenoid.
• Details of the calculation:
  Near the center of the solenoid B = μ₀nI = 4π10^-7(1000/0.4)I T, with I in units of Ampere.
  With B = 10^-4 T, we need I = 10^-4 A/(4π10^-72500) = 31.8 mA.
  (We have to assume that the length of the solenoid is much greater than its diameter, since not enough information is given for a more accurate calculation.)