Ampere's law

Problem:

Find an expression for the magnitude of the magnetic field B as a function of distance r from the center of a long, straight cylindrical conducting wire of radius R that carries a current I of uniform density.  Consider both r < R and r > R.

Solution:

• Concepts:
  Ampere's law
• Reasoning:
  The problem has enough symmetry to find B using Ampere's law alone.
• Details of the calculation:
  r < R:  B(r) = μ₀πr²j/(2πr) =  μ₀rj/2.
  j = I/(πR²),  B(r) = μ₀rI/(2πR²).
  r > R:  B(r) = μ₀I/(2πr).
  If the current is flowing in the z-direction, then the direction of B is the φ-direction.

Problem:

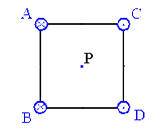
Four long parallel wires carry equal currents of I = 5 A.  The figure is an end view of the conductors. The current direction is into the page at points A and B
and out of the page at points C and D.  Calculate the magnitude and direction of the magnetic field at point P, located at the center of the square of edge length 0.2 m.

Solution:

• Concepts:
  Ampere's law, the principle of superposition
• Reasoning:
  We find the magnitude of the magnetic field due to the current in each wire using Ampere's law.  The direction is found using the right-hand rule.  The total field is the vector sum of the fields produced by the currents in the individual wires
• Details of the calculation:
  Let the y-axis point up and the x-axis point towards the right.  At point P, (the origin of the chosen coordinate system) wires A and D each produce a magnetic field of magnitude μ₀I/(2πd) pointing towards wire B.  Here d² = (0.1² + 0.1²) m². 
  Wires C and B each produce a magnetic field of magnitude μ₀I/(2πd) pointing towards wire D.  The y-components of all the fields add, while the x-components cancel.  The total field at point P therefore has magnitude
  4μ₀Isin(45^o)/(2πd) = 80π10^-7sin(45^o)/(2π (0.02)^½) T = 20 μT
  in the negative y-direction.

Problem:

Four long, current-carrying wires in the same plane intersect to form a square 40.0 cm on each side, as shown in the figure.

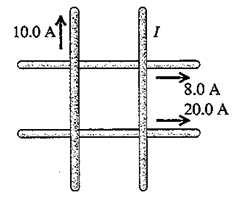
The magnitude and direction of the currents in three wires (arrows' directions are currents' directions) are shown in the figure.
Find the magnitude and direction of the fourth current I so that the magnetic field at the center of the square is zero.

Solution:

• Concepts:
  Ampere's law, the principle of superposition
• Reasoning:
  The center of the square is the same perpendicular distance d away from each wire.
• Details of the calculation:
  Amperes law gives the magnitude of the magnetic field produced by the current in each wire at the center of the square and the right-hand rule gives the direction.  The vector sum of the fields due to the 4 wires is zero.
  Let the z-axis point out of the page, the x-axis towards the right and the y-axis towards the top of the page.  Then the magnetic field due to each wire has only a z-component at the center of the square, B = B_zk.
  0 = -μ₀(10 A)/(2πd) + μ₀(20 A)/(2πd) -  μ₀(8 A)/(2πd) + μ₀(I)/(2πd).
  I = (10 - 20 + 8) A = -2A
  A current of 2 A flows in the negative y-direction.

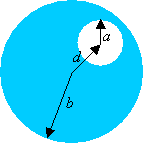
Problem:

An eccentric hole of radius a is bored parallel to the axis of a right circular cylinder of radius b (b > a).  The two axes are at a distance d apart.  A current of I amperes flows in the cylinder.  What is the magnetic field at the center of the hole?  Assume a uniform current density.

Solution:

• Concepts:
  Ampere's law, the principle of superposition
• Reasoning:
  Let the x-axis point towards the right and the y-axis point up.
  A cylinder of radius a carrying a uniform current density -jk superimposed on a cylinder of radius b carrying a uniform current density jk with the center of the smaller cylinder at d presents an equivalent problem.
• Details of the calculation:
  Use Ampere's law:  B(d) = μ₀πd²j/(2πd) =  μ₀dj/2.
  j = I/(π(b² - a²)),  B(d)  =  μ₀Id/(2π(b² - a²)) e_φ = -μ₀I/(2π(b² - a²)))(d × k)
  The direction of B is the φ-direction (right-hand rule).

Problem:

A coaxial cable consists of an inner conductor of radius R = 0.5 m, separated by an outer conductor by a distance ΔR = 0.002 m.  The inner conductor carries a current I = 5 A to the right, and the outer conductor carries the current to the left.  Consider the shaded region of length d between the conductors.

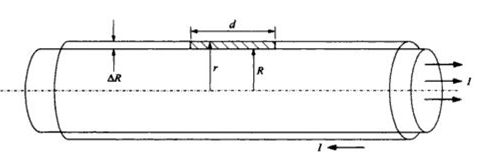
(a)  Find the magnetic field at a point in the shaded region.
(b)  Find the flux of the magnetic field through the shaded region.
(c)  What is the self inductance of the length d of the coaxial cable and the inductance per unit length of the cable?

Solution:

• Concepts:
  Self inductance, Ampere's law, U = ½LI² = (1/(2μ₀))∫ B²dV.
• Reasoning:
  We find the magnetic field produce by the current from Ampere's law and solve
  ½LI² = (1/(2μ₀))∫ B²dV for the self inductance L.
• Details of the calculation:
  (a)  Ampere's law:  B = μ₀I/(2πr) between the conductors.  B encircles the inner conductor according to the right hand rule.  Here r is approximately constant, r = 0.5 m.
  Therefore B = 2*10^-6 T.
  (b)  Flux F = BdΔR = (4*10^-9 Tm)*d
  (c)  L = F/I = 8*10^-10(Tm/A)*d is the self inductance of the length d,
  L = 8*10^-10(Tm²/(Am)) = 8*10^-10 Henry/m.
  Check:  U = ½LI² =  B²d*2πrΔR/(2μ₀),  L = B²d*2πrΔR/(I²μ₀) = 8*10^-10( Henry/m)*d.

Problem:

Find the magnetic vector potential for the case of a long, straight wire carrying a steady current I.  Let R be the radius of the wire.

Solution: 

• Concepts:
  Ampere's law, B = ∇ x A
• Reasoning:
  Ampere's law and symmetry are used to find the field B of a long straight wire.  We then can find a vector potential A so that B = ∇ x A. 
• Details of the calculation:
  Assume the current flows on the z-direction.  Then B is in the φ-direction.
  From Ampere's law (SI units):
  ρ > R:  B = μ₀I/(2πρ),  ρ < R:  B = μ₀jπρ²/(2πρ) = μ₀Iπρ²/(πR² 2πρ) = μ₀Iρ/(2πR²).
  B_φ = (∇ x A)_φ = ∂A_ρ/∂z - ∂A_z/∂ρ = - ∂A_z/∂ρ.  (We cannot have any z-dependence.)
  ρ > R:  ∂A_z/∂ρ = -μ₀I/(2πρ),  A_z = -μ₀I/(2π)ln(ρ/ρ₀)
  ρ < R:  ∂A_z/∂ρ = -μ₀Iρ/(2πR²),  A_z = -μ₀I/(2πR²)(ρ²/2) + C.
  Choose C = 0. Then at ρ = R we have
  μ₀I/(4π) = μ₀I/(2π)ln(R/ρ₀),  ln(R/ρ₀) = ½,  ρ₀ = R*e^-½.

Problem:

(a)  A thin, infinite plane conductor carries a uniform current per unit length j.  Find the magnetic induction B everywhere outside of the plane.
(b)  Find the pressure required to prevent the separation of two such infinite plane conductors oriented parallel to each other and carrying identical but oppositely directed currents.

Solution:

• Concepts:
  Ampere's law
• Reasoning:
  Use Ampere's law and symmetry to find B.  ∮_ΓB∙dr = μ₀I_{through Γ}.
• Details of the calculation:
  (a)  Let the conductor lie in the xy-plane and the current flow in the y-direction..
  
  j = j y/y.  B = B x/x,  z > 0, B = -B x/x,  z < 0,  2Bl = μ₀jl,  B = μ₀j/2.

  (b)  Assume that the second plane conductor is at z = d, with j = -j y/y.
  F = jdx dl x B is the force on a section of the plane of are dxdy = dxdl.
  F/A = jB z/z  = μ₀j²/2 z/z.
  P = F/A = jB = μ₀j²/2.  To keep the planes from separating, the force per unit area on the upper sheet needs to have magnitude μ₀j²/2 and point downward.