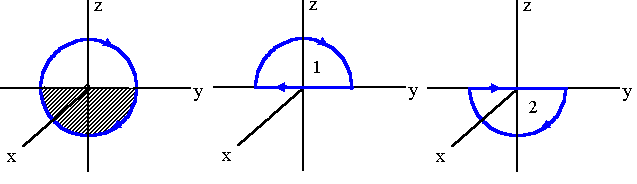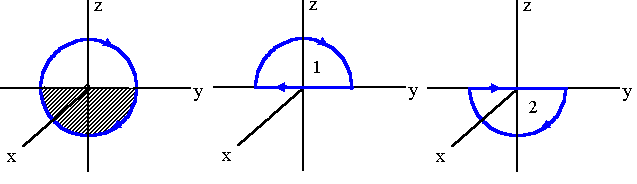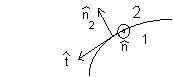Magnetic dipole moment and dipole field

Problem:

A circular loop of wire with radius a = 1 cm and center at the origin is bent, so half lies in the y-z plane and half in the x-y plane.  A current I = 2 A flows in the wire.
(a)  What is the magnetic moment of this loop?
(b)  What is the magnetic field at (x, y, z) = (3, 4, 0) meters from the origin?

Solution:

• Concepts:
  The magnetic moment of a current loop, the principle of superposition, the dipole field
• Reasoning:

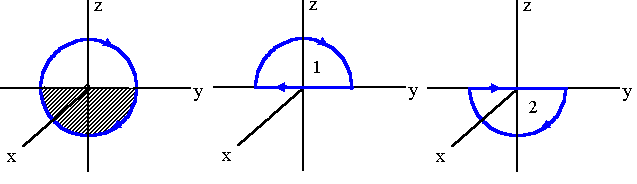
We can view the loop as a superposition of loop 1 and loop 2 as shown.  We find m by adding the moments of loop 1 and loop 2, m = m₁ + m₂.

• Details of the calculation:
  (a)  m₁ = (-i)Iπa²/2,  m₂ = (-k)Iπa²/2, m = (-i - k)Iπa²/2, m = Iπa²/2^½.  (SI units
  The distance from the origin to the point where we want to know the field is much greater that the dimensions of the loop.  The magnetic field is therefore the dipole field.
  B(r) = (μ₀/4π)(3(m·r)r/r⁵ - m/r³),  r = 3i + 4j,  r = 5.
  m∙r = -3Iπa²/2,  (m∙r)r = (-9Iπa²/2)i + (-6Iπa²)j,
  3(m∙r)r/r² - m = (-27Iπa²/50)i - (18Iπa²/25)j + (i + k)Iπa²/2
  = [(-2/50)i - (18/25)j + ½k)]Iπa².
  B(r) = (μ₀/4π)(Iπa²/50)[-i - 36j + 25k]/125
  = (10^-7/125)(2π10^-4/50)[-2i - 36j + 25k] = 10^-14 [-2i - 36j + 25k].

Problem:

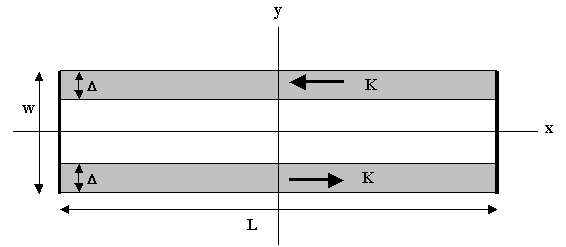
A thin rectangular sheet of composite material has dimensions L x w with L >> w.  The sheet carries a steady surface current that circulates as shown.
A surface current density K = dI/dy = constant flows in the x direction over a width ∆.  At the ends of the rectangle (x = ± L/2) a high conductance "short circuit" completes the current path.
(a)  Find the magnetic moment m.
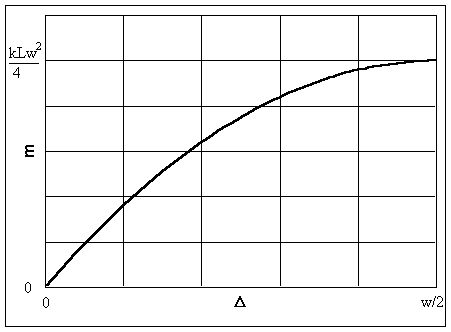
(b)  Sketch the magnitude of m as a function of the width ∆ of the current.

Solution:

• Concepts:
  The magnetic moment
• Reasoning:
  We are asked to find the magnetic moment of a current distribution.
  When you get a problem that asks you to find the magnetic moment of a current distribution, the method that you should think of first is using the principle of superposition.  Try to divide the current distribution into individual flat current loops with magnetic moment m = IAn, and add (integrate) the magnetic moments of the loops (vector addition).
• Details of the calculation:
  (a)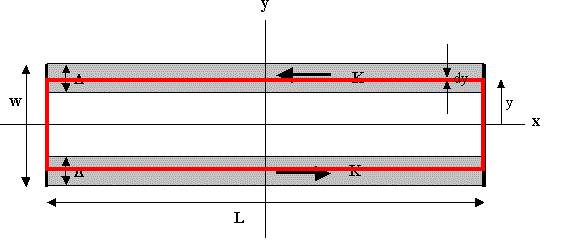
  
  Consider a loop as shown above.  For this filamentary loop dm = k(Kdy)2Ly.
  m =  ∫dm =  k ∫_w/2-∆^w/2dy 2KLy = k KL∆ (w - ∆).
  (b) 
  

Problem:

Assume a "Bohr-type model" of the He atom.   Each electron is in circular orbit of radius 3.95*10^-11 m around a nucleus with effective charge Z_eff = 1.34.
The electrons orbit in a plane perpendicular to the z-axis, with opposite sense of rotation.
(a)  What is the magnitude of the magnetic moment of each electron due to its motion?
(b)  What is the total magnetic moment of the atom?  (Ignore spin.)
(c)  Assume a magnetic field B = B₀k is turned on.  If the radius of the electron orbits does not change, but the electron speed changes by ±dv, what is the total magnetic moment of the atom now (ignoring terms higher than first order in dv)?

Solution:

• Concepts:
  The magnetic moment, the Lorentz force, F = q(E + v x B)
• Reasoning:
  The Coulomb force is the only radial force responsible for  the centripetal acceleration when no magnetic field is present.
  If a magnetic field is turned on F_m = qv x B also contributes.  For the electron moving ccw in the xy-plane the F_total > F_Coulomb and for the electron moving cw in the xy-plane the F_total > F_Coulomb.
• Details of the calculation:
  (a)  For each of the electrons M_ev²/r = k_eZ_effq_e²/r², v² = k_eZ_effq_e²/(M_er), v = 2.93*10⁶ m/s.
  m = IA.  I = q_ev/(2πr) = amount of charge that passes a point on the orbit per unit time.
  m = q_evπr²/(2πr) = q_evr/2 = 9.26*10^-24 J/T.
  (b)  m_total = 0. The magnetic moment of the cw moving electron points into the +k direction while the magnetic moment of the ccw moving electron points into the -k direction.
  (c)  M_e(v + dv)²/r = k_eZ_effq_e²/r² ± q_e(v + dv)B₀
  2M_ev dv/r = ±q(v + dv)B₀,  dv ≈ ±q_eB₀r/(2M_e), ignoring terms in (dv)².
  For the ccw moving electron: dm = q_edvr/2 = +q_eB₀²r²/(4M_e).  The magnitude of the magnetic moment pointing in the -k direction increases.
  For the cw moving electron: dm = -q_edvr/2 = -q_eB₀²r²/(4M_e).  The magnitude of the magnetic moment pointing in the +k direction decreases.
  m_total = -2q_eB₀²r²/(4M_e)k.
  m_total is anti-parallel to B.

Problem:

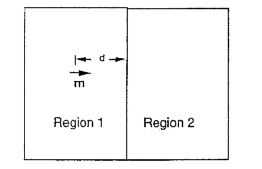
A point magnetic dipole m in vacuum (region 1 in the diagram below) is pointing toward (and is normal to) the plane surface of a material with permeability μ (region 2).  The distance between the dipole and the surface is d.
(a)  Use the method of images to find the magnetic field B in both regions, as follows:  Place an image dipole m' = αm a distance d into medium 2 and take the field B₁ in region 1 to be due to dipoles m and m' in a medium with μ₀.  Take the field B₂ in region 2 to be due to a single dipole m" = βm at the location of the real dipole m in a medium with μ.  Solve the boundary value problem at the interface to evaluate B₁ and B₂.
(b)  Describe physically how each of the image dipoles m' and m" arise and the role they play in determining the fields and the forces on the real dipole and the material of medium 2.
(c)  Evaluate the force acting on the dipole m.

Solution:

• Concepts:
  The magnetic field of a dipole
• Reasoning:
  For a dipole at r' in a medium with permeability μ we have
  B(r) =  (μ/(4π))[3(m∙r'')r''/r''⁵ - m/r''³],  with r'' = r  - r'.
  We must find the superposition of two dipole fields which satisfies the boundary conditions at the interface.
• Details of the calculation:
  (a)  Assume that in region 1 B is the same as that of a dipole m = mk at z = -d and a dipole αmk at z = d.
  Assume that in region 2 B is the same as that of a dipole βmk at z = -d.  Let the z = 0 plane be the boundary between regions 1 and 2.
  Boundary conditions at z = 0:
  
  B₁∙n₂ = B₂∙n₂,  the normal component of B is continuous.
  H₁ x n = H₂ x n,  the tangential component of H is continuous.
  Let r = xi specify a location in the xy-plane, then
  B₁(x,0,0)∙k = (μ₀/(4π))[3md²/(x² + d²)^5/2 - m/(x² + d²)^3/2]
  + (μ₀α/(4π))[3md²/(x² + d²)^5/2 - m/(x² + d²)^3/2].
  B₁∙n = B₁∙k = (1 + α)(μ₀/(4π))[3md²/(x² + d²)^5/2 - m/(x² + d²)^3/2]
  B₂∙n = B₂(x,0,0)∙k = (μβ/(4π))[3md²/(x² + d²)^5/2 - m/(x² + d²)^3/2]
  To satisfy the boundary conditions we need (1 + α)μ₀ = μβ.
  H₁∙i = (1/(4π))[3mdx/(x² + d²)^5/2] - (α/(4π))[3mdx/(x² + d²)^5/2]
  = (1 - α)(1/(4π))[3mdx/(x² + d²)^5/2]
  H₂∙i = (β/(4π))[3mdx/(x² + d²)^5/2]
  To satisfy the boundary conditions we need (1 - α) = β,  (1 + α)μ₀= (1 - α)μ.
  Therefore α = (μ - μ₀)/(μ + μ₀),  β = 2μ/(μ + μ₀).
  The field everywhere in region 1 is
  B(r) =  (μ₀/(4π))[3(m∙r₁)r₁/r₁⁵ - m/r₁³
  + ((μ - μ₀)/(μ + μ₀))(3(m∙r₂)r₂/r₂⁵ - m/r₂³)],
  with r₁ = r + di,  r₂ = r - di.
  The field everywhere in region 2 is
  B(r) =  (2μ/(μ + μ₀))(μ/(4π))[3(m∙r₁)r₁/r₁⁵ - m/r₁³].
  (b)  The field of the dipole m magnetizes the material.  This produces magnetization currents.
  j_m = ∇×M,   k_m = M×n.
  Here j_m = 0, the magnetization currents are surface currents.  This surface current density produces the fields in region 1 that are attributed to the image dipole αm.  In region 2 the dipole m and the surface currents together produce the same field as the image dipole βm.
  (c)  The force on the dipole m is  F = ∇(B∙m), where B is the field due to the image dipole αm at the location of m.
  B(-dk) = (μ₀/(4π))((μ - μ₀)/(μ + μ₀)(2m/(2d)³)k.
  B∙m = -(μ₀/(4π))((μ - μ₀)/(μ + μ₀)(2m²/(2z)³)|_z=-d. 
  ∇(B∙m)|_z=-d = (3μ₀/(4π))((μ - μ₀)/(μ + μ₀)(2m²/8d⁴)k
  = (μ₀/(4π))((μ - μ₀)/(μ + μ₀)(6m²/8d⁴)k.
  F = (μ₀/(4π))((μ - μ₀)/(μ + μ₀)(6m²/8d⁴)k.