Magnetostatic energy

Problem:

A permanent magnet has circular pole pieces of radius a separated by an arbitrary distance.  The magnetic field B is uniform between the pole pieces.  Calculate the force between the pole pieces in terms of B and a.

Solution:

• Concepts:
  Energy stored in the magnetic field
• Reasoning:
  F = -dU/dx.
• Details of the calculation:
  The magnetic field is confined to the region between the pole pieces.  The energy stored in the field is U = (2μ₀)^-½∫_{all space}B²dV in SI units.  Here U = (2μ₀)^-½B²πa²x, where x denotes the distance between the pole pieces.  F = -dU/dx = -(2μ₀)^-½B²πa².  The minus sign indicates that the force is attractive.

Problem:

A solenoid is designed to store U_L = 0.10 J of energy when it carries a current of I = 450 mA. 
The solenoid has a cross-sectional area of A = 5.0 cm² and a length l = 0.20m. 
How many turns of wire must the solenoid have?

Solution:

• Concepts:
  The magnetic field inside a solenoid, magnetostatic energy
• Reasoning
  Approximation:  B = μ₀nI inside the solenoid,  B = 0 outside.
  U = (2μ₀)^-½∫_{all space}B²dV.
  The integral over all space reduces to an integral over the volume of the solenoid.
• Details of the calculation:
  U_L = (1/(2μ₀))B²V = μ₀n²I²lA/2.
  2U_L/( μ₀I²lA) = n²,  n = 88654.  N = nl = 17731.
  or
  U_L = ½LI²,  L = nlBA/I = μ₀n²lA,  n² = 2U_L/( μ₀I²lA).

Problem:

A spiral spring has N turns and initial length x₀.  How does its length changes if a small current I is made to flow through it?  Assume that the spring has a spring constant k for longitudinal deformations, that it can be treated as a perfect ("infinitely long") solenoid, and that its radius R remains fixed.

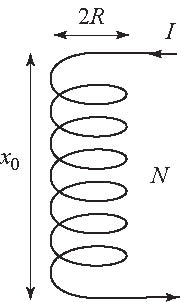
Solution:

• Concepts:
  In equilibrium F_net = 0.
• Reasoning:
  Adjacent coils of the spring attract each other.  The spring gets shorter.  As the spring contracts, the energy stored in the magnetic field changes and the battery maintaining the current I does work. 
  The mechanical work done by the system is  ΔW_mech = ΔW_batt - ΔU_mag.  In equilibrium we need F_net = 0, or dW_mech/dx  = F_ext = kΔx.
• Details of the calculation:
  Given:  I is small, Δx is small, the length of the spring changes little from x₀.
  Let the x-axis point upward.
  Assume the current I is established in a spring of length x₀.
  The magnetic field inside the spring is uniform and has magnitude B = μ₀IN/x₀.
  The energy stored in the field is U_mag = B²V/(2μ₀) = B²πR²x₀/(2μ₀) = μ₀I²N²πR²/(2x₀).
  Assume the length of the spring changes by a small amount Δx.
  For a small displacement the energy stored in the field changes by
  ΔU = dU/dx|_x0Δx = -[μ₀I²N²πR²/(2x₀²)]Δx.
  The energy stored in the field increases when x decreases.
  [We know the coil will contract, but the stored field energy increases when the coil contracts.  How can this be?]
  The flux through the coils is NBπR².  When x changes, B changes, and therefore the flux changes and an emf is induced. 
  In the small time interval Δt we have emf = -NπR²ΔB/Δt.
  The extra work done by the battery to keep the current I flowing is emf*I*Δt = I*NπR²ΔB.
  For  a small displacement ΔB = dB/dx|_x0Δx, so ΔW_batt = -[μ₀I²N²πR²/x₀²]Δx = 2ΔU.
  When x decreases the battery has to do extra work against the induced emf to keep the current constant at I.  (Lenz's rule)
  But when x decreases, only ½ of the work the battery does ends up being stored as field energy.  The other half goes into mechanical work done on the system, which can be stored as elastic potential energy or converted to kinetic energy, or dissipated through friction or radiation.
  The mechanical work done by the system is ΔW_mech = ΔW_batt - ΔU_mag  = -[μ₀I²N²πR²/(2x₀²)]Δx.
  When x decreases, ΔW_mech is positive.
  When the system is in equilibrium if the net force is zero.
  In equilibrium dW_mech/dx = -μ₀I²N²πR²/(2x₀²) = kΔx.
  Δx = -μ₀I²N²πR²/(2kx₀²).
  
  Why do we look at the force, and not just the energy?
  ΔW_mech  = -[μ₀I²N²πR²/(2x₀²)]Δx.
  When the coil has contracted by Δx and is in equilibrium after any oscillation have damped out, not all the mechanical work done is stored as elastic potential energy.
  In this example F_ext = dW_mech/dx is constant. 
  The work done on the system by the external force to is W_mech = ∫₀^Δx F_extdx = F_extΔx.
  (With our orientation of the x-axis, both F_ext and Δx are negative, W_mech is positive.)
  But F_ext = kΔx, so W_mech =  kΔx².  The elastic potential energy stored in the spring is ½kΔx² = ½W_mech.