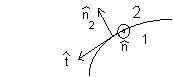Magnetic materials

Problem:

A ferromagnet is one for which the magnetization M(r) is given and the free current density j_f = 0.
(a)  For this case, write down the relevant Maxwell equations for the magnetic induction B and the magnetic field H in the absence of any time-varying electric field.
(b)  For this ferromagnet relate B, H, and M.
(c)  Define the magnetic scalar potential Φ_M and state why this is a valid concept in this case.
(d)  Show that ∇²Φ_M can be expressed in terms of M by a Poisson equation and give its formal solution in the absence of boundaries by comparing with the solution of the electrostatic Poisson equation.

Solution:

• Concepts:
  Magnetostatics, magnetic materials
• Reasoning:
  Starting from Maxwell's equations we derive an expression for the magnetic scalar potential for permanent magnets.
• Details of the calculation:
  (a)  ∇∙B = 0,  ∇ × B = μ₀j,  j = j_f + j_m,  j_m = ∇ × M.
  H = B/μ₀ - M,  ∇ × H = j_f.
  Since j_f = 0 we have ∇∙ B = 0,  ∇ × H = 0.
  (b)  H = B/μ₀ - M.
  (c)  The curl of H is zero everywhere, therefore we may write H = -∇Φ_M.

  (d)  ∇∙ H = ∇∙B/μ₀ - ∇∙M.
  Therefore ∇²Φ_M = ∇∙M.
  In electrostatics, the solution to the Poisson equation ∇²Φ = -ρ/ε₀ in free space is
  Φ(r) = [1/(4πε₀)]∫ρ(r') dV'/|r - r'|.
  The same equations have the same solutions. 
  Φ_M(r) = [-1/(4π)]∫∇∙M(r') dV'/|r - r'|.

Problem:

A sphere of linear magnetic material is placed in an originally uniform magnetic field magnetic field B₀.  Find the new field inside the sphere.

Solution:

• Concepts:
  The uniqueness theorem, boundary conditions, B = μH.
• Reasoning:
  The external magnetic field will magnetize the sphere.  The magnetic field of a uniformly magnetized sphere is uniform inside the sphere (B = 2Mμ₀/3) and a pure dipole field outside the sphere.  Assume that the total field inside the sphere is the superposition of the field of a uniform magnetized sphere and the constant external field B₀.  The superposition of these two fields fulfills all the boundary conditions for B,
  (B₂ - B₁)·n₂ = 0,  (B₂ - B₁)·t₂ = μ₀k·n,
  on the surface of the sphere.
  
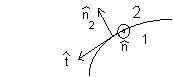
  We have a unique solution as long as inside B = μH = μ₀(1 + χ_m)H inside the sphere.
  B = μH determines the magnetization surface current density.
• Details of the calculation:
  B_in = B₀ + 2Mμ₀/3,  μH_in = B_in,  M = χ_mH_in = (χ_m/μ)B_in.
  (1 - 2μ₀χ_m/(3μ))B_in = B₀.  B_in = B₀(3 + 3χ_m)/(3 + χ_m).
  The magnetic moment of the sphere is m = (4πR³/3)M = (4πR³/3)(χ_m/μ)B_in, where R is the radius of the sphere.  For r > R we have
  B_out = B₀ + (μ₀/4π)[3(m∙r)r/r⁵ - m/r³].

Problem:

A small spherical cavity of radius a is made in a permanent magnet of uniform magnetization M.   Find B and H at the center of the cavity.

Solution:

• Concepts:
  The principle of superposition
• Reasoning:
  Maxwell's equations are linear equations.  The principle of superposition holds.  We may write
  B_cavity = B_material - B_{uniformly magnetized sphere}.
• Details of the calculation:
  For a uniformly magnetized sphere we have:
  B_out = pure dipole field,  B_in = uniform, in the direction of M.
  Let M = Mk, m = (4/3)πa³M.  B_out = (μ₀/4π)[3(m∙r)r/r⁵ - m/r³].
  B_{out_θ} = (μ₀/4π)(m/r³)sinθ,  B_{out_r} = (μ₀/4π)(2m/r³)cosθ.
  B_in = B_ink.  B is continuous at r = ak.
  B_in = (μ₀/4π)(2m/a³)k = (μ₀/4π)(8/3)πM.
  We therefore have B_cavity = B_material - (μ₀/4π)(8/3)πM.
  B_material depends on the shape of the magnetized material.
  H_cavity =  B_cavity/μ₀.

Problem:

A short cylinder (length l and radius a) of iron is magnetized along the axis of the cylinder.  Calculate H and B on the axis, both inside and outside.

Solution:

• Concepts:
  Magnetization M, magnetization current densities, the field of a solenoid
  j_m = ∇×M,  k_m = M×n. 
• Reasoning:
  Magnetization always results in magnetization current densities.  Uniform magnetization results in surface current densities.  The uniform magnetization of a cylinder results in a surface current density like that of a solenoid.
• Details of the calculation:
  For a solenoid we have B_z = (μ₀In/2)(cosθ₁ - cosθ₂).
  (We choose the symmetry axis to be the z-axis,)
  
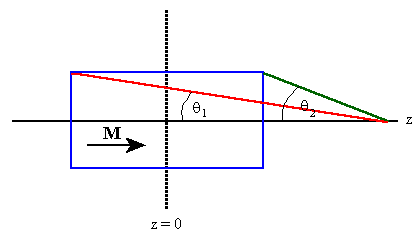
  (I*n) is the current per unit length, i.e. the surface current density.
  For the magnetized cylinder we therefore have on the axis B_z = (μ₀k_m/2)(cosθ₁ - cosθ₂).
  k_m = M (z/z) ×(ρ/ρ) = M (φ/φ).  B_z = (μ₀M/2)(cosθ₁ - cosθ₂).
  If the center of the cylinder is at the origin then
  cosθ₁ = (z + l/2)/(a² + (z + l/2)²)^½,  cosθ₂ = (z - l/2)/(a² + (z - l/2)²)^½.
  H =  B/μ₀ outside.  H =  B/μ₀ - M inside.  H = k[(M/2)(cosθ₁ - cosθ₂) - M] inside.
  At z = l/2 + e (e --> 0) we have H = k(M/2)cosθ₁,  H points into the positive z-direction.
  At z = l/2 - e (e --> 0) we have H = k[(M/2)cosθ₁ - M],  H points into the negative z-direction.
  H reverses direction at the boundary
  Remember:  The same current distributions produce the same fields.
  The normal component of H is not continuous, ∇∙H ≠ 0 in general.

Problem:

A coil of N turns is wrapped around an iron ring of radius d and cross section A (d >> A^½).  Assume a constant permeability μ >> 1 for the iron.

(a)  What is the magnetic flux Φ = ∫B∙dA as a function of current I?
(b)  If a gap of width b, (b² << A) is cut in the ring, what is the flux for the same current I?
(c)  What is the field energy in the iron and in the gap?
(d)  With such a gap in the ring, what is the self inductance?

Solution:

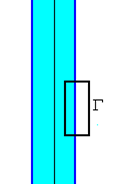
• Concepts:
  Ampere's law for H, ∮_Γ H∙dl = I_{free through Γ},  H = B/μ₀ - M,  magnetic field energy, self inductance
• Reasoning:
  The problem has enough symmetry to let us calculate H from Ampere's law of H alone.
  Iron is not a lih material, but we assume that for the field strength B given in the problem we may write B = μH.  After a small gap has been cut into the ring we use the boundary conditions for B to find B and H in the gap.  We use the energy density u = ½B∙H to find the stored energy.
• Details of the calculation:
  (a)  H and B point into the φ direction,  H = NI/(2πr), B = μNI/(2πr).
  
  If d >> A^½, then B inside the coil is nearly constant,  B = μNI/(2πd).
  Flux Φ = ∫B_ndA,  Φ = μN²IA/(2πd),  Φ is proportional to I.
  (b)  If b² << A, then B_iron ≈ B_gap = μ₀H_gap, because the normal component of B is continuous.
  H_iron(2πd - b) + H_gapb = NI,  (B/μ)(2πd - b) + (B/μ₀)b = NI, from Ampere's law for H.
  B = μμ₀NI/[μ₀(2πd - b) + μb],  Φ = μμ₀N²IA/[μ₀(2πd - b) + μb].
  (c)  The energy density u = ½B∙H =  (1/(2μ))B².
  The field energy in the iron is
  U_iron = A(2πd - b)(μ/2)(μ₀NI/[μ₀(2πd - b) + μb])².
  The field energy in the gap is
  U_gap = Ab(μ₀/2)(μNI/[μ₀(2πd - b) + μb])².
  U_iron + U_gap = ½μμ₀N²I²A/[μ₀(2πd - b) + μb].
  (d)  Φ = LI or U = ½LI² yield L = μμ₀N²A/[μ₀(2πd - b) + μb].
  
  Comment:
  When you are confronted with a small gap between opposite magnetic poles, you make the same approximation that you make when you are confronted with a small gap between large oppositely charged plates (parallel plate capacitor).  You assume that the field in the gap is uniform and neglect edge effects.
  In this problem you again use Ampere's law for H.  Remember that the normal component of B is continuous, but the normal component of H is not.

Problem:

An infinitely long straight wire carrying a steady current I, lies along the axis of a linear paramagnetic cylinder of radius R and permeability μ. 
(a)  Find H, B and M inside and outside the cylinder.
(b)  Compute all bound currents flowing in the cylinder.

Solution:

• Concepts:
  Ampere's law for H,  ∮_Γ H∙dl = I_{free through Γ},  H = B/μ₀ - M
• Reasoning:
  The problem has cylindrical symmetry.  We can find H from Ampere's law alone.
  For linear, isotropic, homogeneous (lih) magnetic materials we have
  M = Χ_mH,  B = μ₀(H + M) = μ₀(1 + Χ_m)H =  μ₀κ_mH =  μH.
• Details of the calculation:
  (a)  Let the current flow along the z-axis in the +z direction.
  H = I/(2πr) (φ/φ) .
  For 0 < r < R, M = (μ/μ₀ - 1)I/(2πr) (φ/φ)  ,  B = μI/(2πr) (φ/φ) , 
  For r > R, M = 0, B = μ₀I/(2πr) (φ/φ) 
  (b)  j_m = ∇×M,  k_m = M×n.
  M = M_φ (φ/φ),  ∇×M = k (1/r)∂rM_φ/∂r = 0.
  ∇× M is undefined at r = 0.  I_m = ∫_A(∇×M)∙ndA = ∫_loopM∙ds = (μ/μ₀ - 1)I.
  In addition to the current I in the wire, a magnetization current (μ/μ₀ - 1)I is flowing in the k direction in the center.
  Along the surface at r = R we have a surface current k_m = (μ/μ₀ - 1)I/(2πR) (-k).
  A magnetization current (μ/μ₀ - 1)I is flowing in the -k direction along the surface of the magnetic material.

Problem:

An infinitely long cylinder of radius R carries a "frozen in" magnetization parallel to the axis, M = kr, where k is constant and r is the distance from the axis. 
(a)  Find B and H inside and outside the cylinder.
(b)  Find the magnetic vector potential inside and outside the cylinder.

Solution:

• Concepts:
  Magnetization currents, Ampere's law for H
• Reasoning:
  Let the symmetry axis of the cylinder be the z-axis.  Then the volume magnetization current density j_m = ∇ × M has only a φ component,
  j_mφ = -∂M/∂r = -k.  The surface magnetization current density k_m = M × n  also has only a φ component, k_mφ = kR.
   
• Details of the calculation:
  
  (a)  The problem is equivalent to that of a set of infinitely-long, nested coils.  We therefore know that for r > R B = H = 0.  For r < R B and H can only have z-components, and we can solve the problem using Amperes law for H.  The contour integral of the tangential component of H along the close loop Γ must be zero, H = 0 everywhere.
  Inside the magnetized material  B = μ₀(H + M), B = μ>₀M.

  (b)  B = ∇ × A.  Symmetry suggests that A can be chosen to only have a φ component.
  Stoke's theorem: ∫_{area S} (∇ × A) ·n dS = ∫B·n dS  =  ∫_ΓA·dr = ∫_ΓA_φ r d φ = 2πrA_φ.
  Inside: ∫B·n dS  = ∫₀^r μ₀kr 2πr dr = μ₀2πk r³/3.
  A_φ = μ₀k r²/3.
  Outside: ∫B·n dS  = ∫₀^R μ₀kr 2πr dr = μ₀2πk R³/3.
  A_φ = μ₀k R³/(3r).

Problem:

At saturation, when nearly all of the atoms have their magnetic moments aligned, the magnetic field in a sample of iron can be 2 T.  If each electron contributes a magnetic moment of one Bohr magneton, how many electrons per atom contribute to the saturated field of the iron?
(Iron: ~8.5*10²⁸ atoms/m³)

Solution:

• Concepts:
  The saturation magnetization M_sat,  B = μ₀(H + M).
• Reasoning:
  M_sat = Nmk, for a magnetic field pointing in the z direction.  Here m is the magnitude of the magnetic moment of each atom and N is the number of atoms per unit volume.
  At saturation  B = μ₀M_sat.
• Details of the calculation:
  The magnetization M is defined as the magnetic dipole moment per unit volume.
  M = 8.5*10²⁸ atoms/m³*n*9.27*10^-24 Am².
  Here n is the number of electrons per atom that contribute to the saturated field of the iron and 9.27*10^-24 Am² is the Bohr magneton in SI units.
  2 T = 4π*10^-7(Tm/A)*8.5*10²⁸ m^-3*n*9.27*10^-24 Am²,
  n = 2.