Resistors in series and parallel, Kirchhoff's rules

Resistors in series and parallel

Problem:

Four identical light bulbs of resistance R are connected as shown in the figure. 

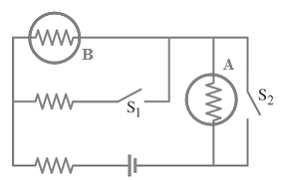
The battery provides a potential difference V₀.  The switches S₁ and S₂ can be open and/or closed in four different combinations: open-open, closed-closed, open-closed, closed-open.
(a)  Consider light bulb A:  determine which switch combinations would produce the brightest and dimmest light in bulb A.
(b)  Consider light bulb B:  determine which switch combinations would produce the brightest and dimmest light in bulb B.

Solution:

• Concepts:
  Resistors in series and parallel
• Reasoning:
  Analyze a simple circuit.
• Details of the calculation:
  (a)        brightest:  S₁ closed, S₂ open, I_A = 2V/(5R).
  dimmest:  S₂ closed,  I_A = 0.
  (b)        brightest:  S₂ closed, S₁ open, I_B = V/(2R).
  dimmest:  S₁ closed, S₂ open, I_B = V/(5R).

Problem:

The circuit shown in the diagram contains an ideal battery and two resistors, R₁ and R₂.
A voltmeter is used to measure the voltage across R₁, then across R₂, then across the battery.
Its readings are, respectively, 2.0 V; 3.0 V; 6.0 V.

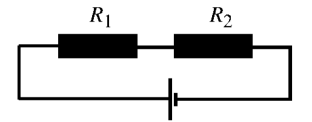
What are the actual voltages across the resistors?

Solution:

• Concepts:
  Resistors in series and parallel
• Reasoning:
  The voltmeter as has a shunt resistance R.  It reads the voltage across this resistance.  When placed in a circuit, it correctly reads the battery voltage but not the voltages across the resistors of the undisturbed circuit.
  The battery voltage is V = 6 V.
  The voltages across R₁ and R₂ (without the voltmeter in the circuit) are
  V₁ = 6V R₁/(R₁ + R₂) and V₂ = 6V R₂/(R₁ + R₂), respectively.
  V₁ = 6V /(1 + R₂/R₁), V₂ = 6V /(1 + R₁/R₂).
  We need to solve for the ratio R₁/R₂.
• Details of the calculation:
  With the voltmeter in the circuit we have:
  2V = 6V [R₁R/(R₁ + R)]/[ (R₁R/(R₁ + R)) + R₂] or 2V = 6V/[1 + R₂(R₁ + R)/(R₁R)]
  3V = 6V [R₂R/(R₂ + R)]/[ (R₂R/(R₂ + R)) + R₁] or 3V = 6V/[1 + R₁(R₂ + R)/(R₂R)]
  [1 + R₂(R₁ + R)/(R₁R)] = 3,  R₂(R₁ + R)/(R₁R) = 2,  R₂/R + R₂/R₁ = 2,  1/R = 2/R₂ - 1/R₁
  [1 + R₁(R₂ + R)/(R₂R)] = 2,  R₁(R₂ + R)/(R₂R) = 1,  R₁/R + R₁/R₂ = 1.  1/R = 1/R₁ - 1/R₂
  Therefore 3/R₂ = 2/R₁,  R₁/R₂ = (2/3).
  V₁ = 6V *2/5 = 2.4 V,  V₂ = 6V*3/5 = 3.6 V.

Problem:

What is the resistance of the following network?  Each ohmic resistor has resistance R.

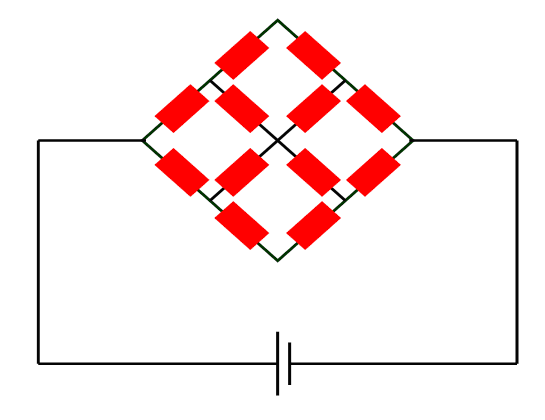
Solution:

• Concepts:
  Resistors in series and parallel
• Reasoning:
  The circuit has enough symmetry so that we can analyze it like a simple circuit with resistors in series and parallel.
• Details of the calculation:
   

  

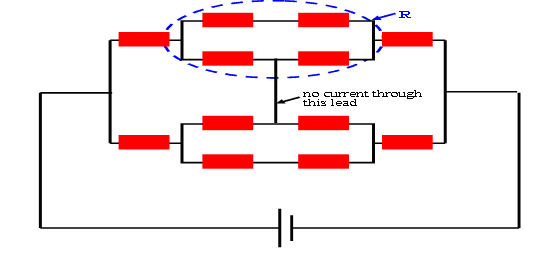
  R_total = (3/2)R.

Problem:

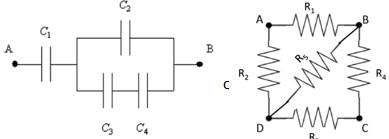
(a)  Four capacitors are connected as shown in the figure.
C₁ = C₂ = C₃ = C₄ = 1 μF.   
What is the total capacitance between points A and B?
(b)  Five identical 1 Ω resistors are joined and form the four sides of square and its diagonal.  What is the resistance between points A and B?

Solution:

• Concepts:
  Capacitors and resistors in series and parallel
• Reasoning:
  We are asked to find the effective capacitance and resistance of given configurations.
• Details of the calculation:
  (a)  The inverse of the equivalent capacitance for the sub-circuit with two capacitors C₃ and C₄ is
  1/C_eq = 1/1 + 1/1 = 2, thus C_eq= ½.   Now, the equivalent capacitance for the sub-circuit with C₂, C₃, and C₄ is C_eq'= C  + C_eq = 1 + ½ = 3/2.   Finally, the equivalent capacitance for the entire circuit is  1/C_eq'' = 1/C₁ + 1/C_eq' = 1 + (2/3) = 5/3, thus C_eq''= 3/5.  The total capacitance is 0.6 uF.

  (b)  The equivalent resistance of a sub-circuit with R₃ and R₄ is 2.  The equivalent resistance of a sub-circuit with R₃, R₄, and R₅ is 1/R_eq =1/1 + ½ = 3/2, thus R_eq = (2/3).  The equivalent resistance of a sub-circuit with R₂, R₃, R₄, and R₅ is R_eq' = R₂ + Re_q  = 1 + (2/3) = 5/3.  Finally, the equivalent resistance of the entire circuit is 1/R_eq''= 1/1 + 3/5 = 8/5, thus R_eq''= 5 /8.  The resistance between points A and B is 5/8 Ω.

Problem:

Find the maximum power of a heating element that can be constructed from a piece of wire that has a resistance of 536 Ω.  The element is to be powered by a constant voltage of V = 110V.  The current through the wire cannot exceed 2.0 A.
(a)  Assume that you are allowed to discard a section of the wire,
(b)  Assume that you are NOT allowed to discard a section of the wire,

Solution:

• Concepts:
  Ohm's law, I = V/R, Power P = IV, resistors in series and parallel
• Reasoning:
  We can cut the wire into N pieces and connect these pieces in parallel to the power supply.
• Details of the calculation:
  Since V is constant, we have to maximize I to maximize P.
  For each of the pieces of wire that are connected in parallel we have
  I = V/R, I_max = 2 A = 110 V /R_min,  R_min = 55 Ω.
  (a)  We can cut 9 pieces of 55 Ω and discard one piece of 41 Ω.
  Then the total current is 9*2 A and the power dissipated is 1980 W.
  (b)  We can cut 8 pieces of 55 Ω and 1 piece of 96 Ω.  The total current them is
  I_total = 8*110 V/(55 Ω) + 110 V/(96 Ω).  The power is P = VI_total = 1886 W.
  But what if we cut some small piece of the 96 Ω wire and added it to one of the 55 Ω wires?
  I = V/R, dI = -(V/R²)dR
  The total change in current through the wires them is dI = -(V/R²_55Ω)dR + (V/R²_96Ω)dR.
  dI is negative, less current flows, less power is dissipated in the heating element.  The maximum power dissipated in the heating element is 1886W.

Problem:

In the infinite circuit shown in the diagram, each battery has emf ε and internal resistance r.  Each resistor has resistance 2r.  Find the emf and the internal resistance of the equivalent battery.

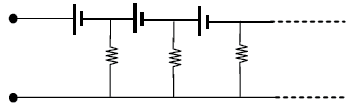
Solution:

• Concepts:
  An infinite ladder network
• Reasoning:
  Since the ladder is infinite, the current through the equivalent emf and internal resistance will not change if an additional section is added to the front of ladder.
• Details of the calculation:
  Any combination of batteries and resistances with two terminals can be replaced by a single voltage source V and a single series resistor R.  The Thevenin voltage V is an ideal voltage source equal to the open circuit voltage at the terminals.  The Thevenin resistance R is the resistance measured at the terminals with all voltage sources replaced by short circuits and all current sources replaced by open circuits.  Let the Thevenin voltage of the network be V am let the Thevenin resistance be R.
  The network is made of an infinite number of sections.
  Let us construct a new two-terminal network by adding another section to the front of the old two-terminal network.

  

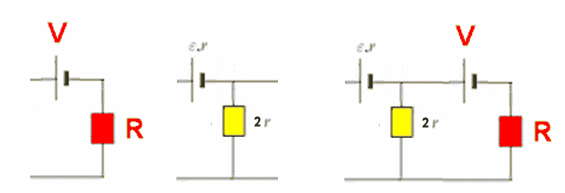
  Let the Thevenin voltage of the new network be V' and let the Thevenin resistance be R'.
  We have
  V' = ε +V2r/(2r + R),  R' = 2rR/(R + 2r) + r = (3rR + 2r²)/(R + 2r).
  Setting R' = R, V' = V we obtain
  R² - rR - 2r² = 0, R = r/2 + ((r/2)² + 2r²)^½ = 2r.
  V = (2r + R)ε/R = 2ε.
  The emf of the equivalent battery is 2ε, and the internal resistance is 2r.

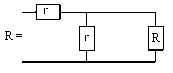
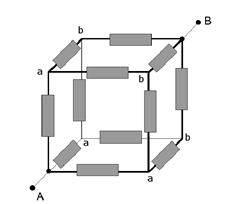
Problem:

(a)  Calculate the resistance between two points A and B of the infinite system of resistors.

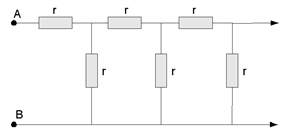
(b)  Calculate the resistance between points A and B of the cube made of identical resistors r.

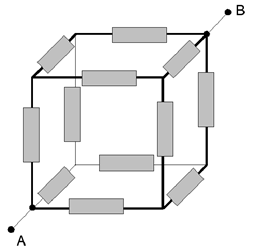
Solution:

• Concepts:
  Resistors in series and parallel, symmetry
• Reasoning:
  We can use symmetry to reduce the given networks to simple networks.
• Details of the calculation:
  (a)  The resistance R of an infinite ladder does not change if we add another section.

  
  R = r + Rr/(r + R).  R = (r/2)(1 + √5).

  (b)
     
  R = r/3 + r/6 + r/3 = 5r/6.

Problem:

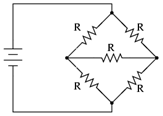
What is the equivalent resistance of the network shown?  Each resistor has resistance R.

Solution:

• Concepts:
  Resistors in series and parallel
• Reasoning:
  No current flows through the center resistor.  It can be ignored.  Then circuit has enough symmetry so that we can analyze it like a simple circuit with two pairs of resistors in series. The pairs are parallel to each other.
• Details of the calculation:
  For two resistors in series:  R_eff = R₁ + R₂.
  For two resistors in parallel:  1/R_eff  = 1/R₁ + 1/R₂.
  Each resistor has resistance R, the equivalent resistance is R.

Kirchhoff's rules

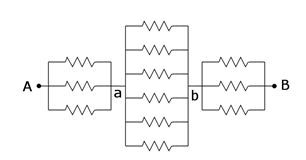
Problem:

Find the equivalent resistance between the points A and B of the circuit shown in the figure below.

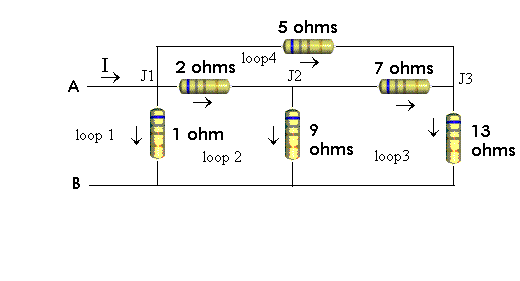
Solution:

• Concepts:
  Kirchhoff's rules
• Reasoning:
  We can find the equivalent resistance using Kirchhoff's rules.  The junction rule states that the sum of the currents entering a junction must equal the sum of the currents leaving that junction.  The loop rule states that the sum of the potential differences around any closed circuit loop must be zero.
  Assume some direction for the current flowing in each part of the circuit.  

  • If a resistor is traversed in the direction of the current, the change in potential across the resistor is -IR.

  • If a resistor is traversed in the direction opposite to that of the current, the change in potential across the resistor is +IR.

  • If a voltage source is traversed in the direction from - to +, the change in potential is +V.

  • If a voltage source is traversed in the direction from + to -, the change in potential is -V.

  We can use the junction rule as many times as it is possible to include in it a current that has not been used in a previous junction rule equation.  The number of equations must be equal to the number of unknowns.

• Details of the calculation:
  Assume you connect a battery between A and B so that A is at some voltage V and B is at ground.  A current I will start flowing through the circuit from A to B.  V = IR, R = V/I.  If you know I, then you know R.
  
  To find R for the circuit we need to know the currents flowing through the 6 resistors.  Let I(1) denote the current flowing through the 1 ohm resistor, I(2) denote the current through the 2 ohm resistor, and so on.  The total current leaving point A is denoted by I.  We need to use Kirchhoff's rules to find 7 equations for the seven currents, and then use algebra to solve those seven equations simultaneously.
  (1) For the junction labeled J1 we have I(1) + I(2) + I(5) - I = 0.
  (2) For the junction labeled J2 we have I(2) - I(7) - I(9) = 0
  (3) For the junction labeled J3 we have I(13) - I(7) - I(5) = 0
  (4) For loop 1 we have V - 1*I(1) = 0
  (5) For loop 2 we have 1*(I1) - 2*I(2) - 9*I(9) = 0
  (6) For loop 3 we have 9*I(9) - 7*I(7) - 13*I(13) = 0
  (7) For loop 4 we have 2*I(2) + 7*I(7) - 5*I(5) = 0
  
  Let us now use equation 4 to eliminate I(1) from the other equations.
  I(1) = V.  We now have six equations.
  (1) For the junction labeled J1 we have V + I(2) + I(5) - I = 0.
  (2) For the junction labeled J2 we have I(2) - I(7) - I(9) = 0
  (3) For the junction labeled J3 we have I(13) - I(7) - I(5) = 0
  (5) For loop 2 we have V - 2*I(2) - 9*I(9) = 0
  (6) For loop 3 we have 9*I(9) - 7*I(7) - 13*I(13) = 0
  (7) For loop 4 we have 2*I(2) + 7*I(7) - 5*I(5) = 0
  
  Let us now use equation 2 to eliminate I(2) from the other equations.
  I(2) = I(7)+I(9).  We now have five equations.
  (1) For the junction labeled J1 we have V + I(7) + I(9) + I(5) - I = 0.
  (3) For the junction labeled J3 we have I(13) - I(7) - I(5) = 0
  (5) For loop 2 we have V - 2*I(7) - 11*I(9) = 0
  (6) For loop 3 we have 9*I(9) - 7*I(7) - 13*I(13) = 0
  (7) For loop 4 we have 9*I(7) + 2*I(9) - 5*I(5) = 0
  
  Let us now use equation 3 to eliminate I(5) from the other equations.
  I(5) = I(13)-I(7).  We now have 4 equations.
  (1) For the junction labeled J1 we have V + I(9) + I(13) - I = 0.
  (5) For loop 2 we have V - 2*I(7) - 11*I(9) = 0
  (6) For loop 3 we have 9*I(9) - 7*I(7) - 13*I(13) = 0
  (7) For loop 4 we have 14*I(7) + 2*I(9) - 5*I(13) = 0
  
  Let us now use equation 5 to eliminate I(7) from the other equations.
  2*I(7) = V-11*I(9).  We now have three equations.
  (1) For the junction labeled J1 we have V + I(9) + I(13) - I = 0.
  (6) For loop 3 we have -7*V + 95*I(9) - 26*I(13) = 0
  (7) For loop 4 we have 7*V - 75*I(9) - 5*I(13) = 0
  
  Let us now use equation 7 to eliminate I(9) from the other equations.
  75*I(9) = 7*V - 5*I(13).  We now have 2 equations.
  (1) For the junction labeled J1 we have 82*V + 70*I(13) - 75*I = 0.
  (6) For loop 3 we have 140*V - 2425*I(13) = 0
  
  Let us now use equation 6 to eliminate I(13) from the other equations.
  485*I(13) = 28*V.  We now have 1 equations.
  (1) For the junction labeled J1 we have 41730*V - 36375*I = 0.
  
  I = (41730/36375)*V = 1.147*V
  R = V/I = 0.87 ohms
  
  The resistance is 0.87 ohms.

Problem:

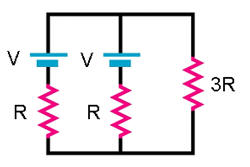
In the circuit above, express the current in the 3R resistor in terms of V and R.

Solution:

• Concepts:
  Kirchhoff's rules
• Reasoning:
  
  
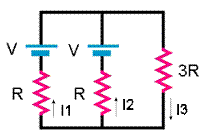
  We can find the currents I₁, I₂, and I₃ using Kirchhoff's rules.  The junction rule states that the sum of the currents entering a junction must equal the sum of the currents leaving that junction.  The loop rule states that the sum of the potential differences around any closed circuit loop must be zero.
• Details of the calculation:
  I₁ + I₂ = I₃,  I₁ = I₂,  V - 3RI₃ - RI₂ = 0.  I₃ = 2V/(7R).