Induced emf and energy

Problem:

A vertically oriented square loop of wire falls from a region where the magnetic field B is horizontal, uniform and perpendicular to the plane of the loop, into a region where the field is zero.  Let the length of each side be s and the diameter of the wire be d.  The resistivity of the wire is ρ_R and the density of the wire is ρ_m.  If the loop reaches terminal velocity while its upper segment is still in the magnetic field region, find an expression for the terminal speed.

Solution:

• Concepts:
  The induce emf ε  = -∂flux/∂t,  Ohms law, energy conservation.
• Reasoning:
  As the loop falls, the flux through the loop changes and an emf is induced in the loop.  This causes a current to flow in the loop, and energy is dissipated in the form of heat.  If the loop falls with constant velocity, then the rate at which the gravitational potential energy decreases must equal the rate at which heat is generated.
• Details of the calculation:
  |emf| = |dflux/dt| = Bsdy/dt,  I = emf/R.  Here dy/dt is the speed with which the loop is falling.
  When terminal speed is reached: I²R = emf²/R = Fv_terminal = mgv_terminal.
  The energy dissipated in the wire per unit time equals the gravitational potential energy lost per unit time.
  (Bsv_terminal)²/R = mgv_terminal,  v_terminal = mgR/(Bs)².
  R = ρ_R16s/πd²,  m = ρ_mπd²s,  v_terminal = 16g ρ_mρ_R/B².

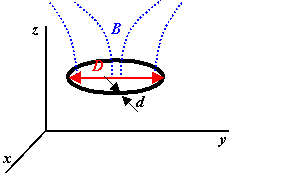
Problem:

A conducting circular loop made of wire of diameter d, resistivity ρ, and mass density ρ_m is falling from a great height h in a magnetic field with a component B_z = B₀(1 + kz), where k is some constant.  The loop of diameter D is always parallel to the x-y plane.  Disregard air resistance, and find the terminal velocity of the loop.

Solution:

• Concepts:
  The induce emf ε  = -∂F/∂t,  Ohms law, energy conservation.
• Reasoning:
  As the loop falls through the inhomogeneous magnetic field, the flux through the loop changes, and an emf is induced in the loop.  This causes a current to flow in the loop, and energy is dissipated in the form of heat.  If the loop falls with constant velocity, then the rate at which the gravitational potential energy decreases must equal the rate at which heat is generated.
• Details of the calculation:
  The gravitational force is in the -z direction, F_g = -mg k.
  The magnetic flux through the loop is F = BA = B₀(1 + kz)πD²/4.
  The emf induced in the loop is ε = -∂F/∂t = -(B₀kπD²/4)dz/dt.
  The current flowing in the loop is I = |ε|/R.
  The rate at which heat is generated is I²R.  The rate at which gravitational potential energy decreases is mg dz/dt
  When dz/dt = -v_t, (v_t = terminal velocity), then I²R = -mg dz/dt = mgv_t.
  Then |ε|²/R  = mgv_t,  [B₀²k²π²D⁴/(16R)]v_t² = mgv_t,  v_t = 16mgR/(B₀²k²π²D⁴).
  m = ρ_mV = ρ_m(πd²/4)πD.  For a wire R = ρ length/area = ρ 4D/d².
  v_t = 16ρ_m(πd²/4)πDg(ρ 4D/d²)/(B₀²k²π²D⁴) = 16ρ_mgρ/(B₀²k²D²).

Problem:

A thin disk of ordinary metal with electrical conductivity σ has radius R and thickness d.  It is held fixed in a perpendicular magnetic field B(t)k = (B₀ + αt)k where B₀ and α are positive constant quantities.  In the following, neglect the self inductance of the disk.  See the sketch.

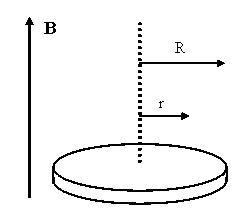
(a)  Find the current density vector j(r) at distance r from the axis of the disk.
(b)  Determine the energy/time delivered to the disk by the field.  What becomes of this energy?
(c)  Suppose that the constant a becomes negative, i.e., that α --> -α.  How do your results in parts (a) and (b) change?

Solution:

• Concepts:
  Faraday's law, Ohms law
• Reasoning:
  Divide the disk into concentric rings.  The magnetic flux through the ring is changing with time.  This flux change induces an emf.  Since the ring has finite resistance, a current flows in the ring.
• Details of the calculation:
  For a ring with inner radius r and outer radius r + dr we have
  ε(r) = -∂F/∂t = induced emf,   ∂F/∂t = (∂B/∂t)пr² = αпr².
  E = αпr²/(2пr) = αr/2.  If α is positive, E points into the -φ direction.
  
  j = σE,  j(r) = σαr/2.
  (b)  The current flowing in the ring with radius r is j(r)*d*dr.  The rate at which energy is delivered to the ring is ε(r)*j(r)*d*dr = (dпr³σα²/2)dr.
  The rate at which energy is delivered to the disk is
  (dпσα²/2)∫₀^Rr³dr = dпσα²R⁴/8.  This energy is converted into thermal energy.
  (c)  E and j now point into the φ direction.  The power delivered to the disk is the same.

Problem:

A uniform magnetic field B = B₀k points in the z-direction.  A particle with mass m and charge q moves with kinetic energy E₀ in the x-y plane in a circular orbit centered at the origin as shown.

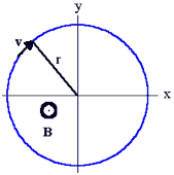
At t = 0 the magnetic field strength starts changing slowly, so that at t = t₁ it is B = B₁k.  Neglect radiation.
(a)  What is the radius of the orbit R₀ of the particle for t < 0 in terms of B₀, and E₀?
(b)  Assuming that the radius R of the orbit of the particle does not change appreciably while the particle completes one revolution, what is the kinetic energy E₁ of the particle at time t₁ in terms of B₀, B₁, and E₀?

Now assume that the magnetic field stays constant (B = B₀k), but that the particle is subject to a drag force F_d = -mv/τ, where τ is a constant.  At time t = 0 the position and velocity of the particle are R₀ = (0, R₀, 0) and v₀ = (v₀, 0, 0).
(c)  Write Newton's equations of motion for the velocity components v_x, v_y, and v_z.
(d)  Construct an equation of motion for z = v_x + iv_y, and solve it. 
(e)  Find expressions for v_x(t), v_y(t), x(t), and y(t).  Describe the trajectory of the particle in words.

Solution:

• Concepts:
  Faraday's law, induced emf, damped oscillations
• Reasoning:
  A changing magnetic flux induces an emf which changes the kinetic energy of the particle.
• Details of the calculation:
  (a)  R₀ = mv/(qB₀) = (2mE₀)^½/(qB₀)
  (b)  Assume that the radius R of the orbit of the particle does not change appreciably while the particle completes one revolution.  Then the particle's kinetic energy changes by
  ΔE = q(dB/dt)πR² over one revolution.
  The time for one gyration is T = 2πR/v,
  so dE/dt = ΔE/T = (qvR/2)(dB/dt) = (qmv²R/(2mv))(dB/dt) = (1/B)(dB/dt)E.
  (We used R = mv/(qB), qR/(mv) = 1/B, ½mv² = E.)
  dE/E = dB/B,  ln(E₁) = ln(B₁E₀/B₀),  E₁ = B₁E₀/B₀.
  (c)  F_x = mdv_x/dt = qv_yB₀ - mv_x/τ,  F_y = mdv_y/dt = -qv_xB₀ - mv_y/τ,  F_z = 0.
  (d)  dz/dt = -i(qB₀/m)(v_x + iv_y) - (v_x + iv_y)/τ = -i(qB₀/m)z - (1/τ) z
   = -i[(qB₀/m)z - (i/τ)]z = gz,
  where g =  -i[(qB₀/m)z - (i/τ).
  z(t) = z₀exp(gt) = z₀exp(-t/τ) exp(-iωt), with ω = qB₀/m.
  (e)  Re(z(t)) = v_x(t) = v₀ exp(-t/τ) cos(ωt),  Im(z(t)) = v_y(t) = -v₀exp(-t/τ) sin(ωt).
  x(t) = ∫₀^t v₀ exp(-t'/τ) cos(ωt') dt'
  = v₀ [exp(-t/τ)[- cos(ωt)/τ + ω sin(ωt)] + 1/τ]/[1/τ² + ω²]
  y(t) = -∫₀^t v₀ exp(-t'/τ) sin(ωt') dt' + R₀
  = -v₀ [exp(t/τ)[ -sin(ωt)/τ - ω cos(ωt)] + ω] /[1/τ² + ω²] + R₀
   As t --> infinity, x(t) --> x_∞ = (v₀ /τ)/[1/τ² + ω²],  y(t) --> y_∞ = -v₀ ω/[1/τ² + ω²] + R₀
  The particle spirals into the point (x_∞, y_∞).

  

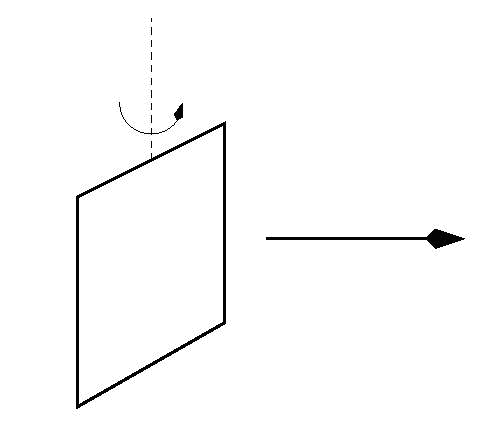
Problem:

A thin metallic square frame of mass m, electrical resistance R, and side a is rotating about an axis perpendicular to a uniform magnetic field B as shown in the figure.  Initially the square frame rotates with a frequency ω₀.
(a)  Determine the average energy loss per cycle due to Joule heating.
(b)  Determine the time it takes for the frequency of the rotation to slow down to 1/e of its initial value.  (Assume that the fractional change in the frame's rotation frequency per cycle is small.)

Solution:

• Concepts:
  The induce emf e  = -∂F/∂t,  Ohms law, energy conservation
• Reasoning:
  A changing magnetic flux produces an emf in the frame.  The emf causes a current to flow which produces Joule heating.  Kinetic energy is converted to thermal energy.
• Details of the calculation:
  (a) (SI units)
  The magnetic flux through the frame is Ba²cosθ.  The angle is changing, dθ/dt = ω.
  The induced emf due to this changing flux is -Ba²sinθ ω.
  The current flowing in the frame is given by I = Ba²sinθ ω/R (neglecting the self inductance of the loop).
  The amount of kinetic energy converted into thermal energy per unit time is P = B²a⁴sin²θ ω²/R.
  Energy loss per cycle (assuming ω changes negligibly):
  ∫₀^T Pdt = ∫₀^2π (P/ω)dθ = πω B²a⁴/R = ΔE.
  Initial average energy loss per cycle due to Joule heating: πω₀ B²a⁴/R.
  <P> = ΔE/T = B²a⁴ω²/(2R).

  (b)  <P> = B²a⁴ω²/2R = -dE/dt.
  E = ½Iω², = ma²ω²/12,  ω² = 12E/ma²,  dE/dt = -E 6B²a²/(Rm).
  E = E₀exp[-6B²a²t/(Rm)],  t_(1/e) = Rm/(6B²a²).