Faradays law/Motional emf

Problem:

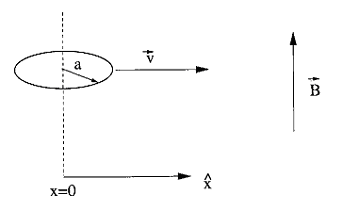
A loop of radius a and mass M made of resistive material has a total resistance R.  At t = 0, the loop is located at x = 0 and moves with velocity v₀ i.  The loop lies in the x-y plane.  There is a magnetic field B = B₀ (x/x₀) k.  How far does the loop travel before stopping?

Solution:

• Concepts:
  Faraday's law
• Reasoning:
  The magnetic flux through a filamentary loop is changing with time.  This flux change induces an emf.  The emf causes a current to flow, which dissipates energy.
• Details of the calculation:
  Flux F = πa²B = πa²B₀x/x₀.  |emf| = ∂F/∂t = (πa²B₀/x₀)∂x/∂t = (πa²B₀/x₀)v.
  I = emf/R.  P = I*emf = emf²/R.  The power dissipated must equal the rate at which the loop looses kinetic energy.
  emf²/R = -Mvd(v/dt).  dv/dt = -bv with b = (πa²B₀/x₀)²/(RM).
  v(t) = v₀exp(-bt).
  The distance the loop travels before stopping is
  d = ∫₀^∞v(t)dt = -(1/b)v₀exp(-bt)|₀^∞  = v₀/b = v₀RMx₀²/(πa²B₀)².

Problem:

(a)  A closed circular coil of N turns, radius a and total resistance R is rotated with uniform angular velocity ω about a vertical diameter in a horizontal magnetic field B₀ = B₀i.  Compute the emf ε induced in the coil, and also the mean power <P> required for maintaining the coil's motion.  Neglect the coil self inductance.
(b)  A small magnetic needle is placed at the center of the coil, as shown in the figure.  It is free to turn slowly around the z-axis in a horizontal plane, but it cannot follow the rapid rotation of the coil.

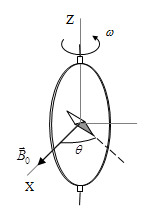
Once the stationary regime is reached, the needle will point in a direction making a small angle θ with B₀.  Compute the resistance R of the coil in terms of this angle and the other parameters of the system.  (Lord Kelvin used this method in the 1860s to set the absolute standard for the ohm.) 

Solution:

• Concepts:
  Induced emf, the magnetic field at the center of a current loop
• Reasoning:
  The changing magnetic flux through the rotating loop produces an emf, which causes a current to flow.  This current produces its own magnetic field.
• Details of the calculation:
  (a)  After some time t, the normal to the coil plane makes an angle ωt with the magnetic field B₀ = B₀i.  Then, the magnetic flux through the coil is Φ = NB∙S, where the vector surface S is given by
  S =  πa²(cos(ωt)i + sin(ωt)j).  Therefore Φ = NB₀πa²cos(ωt).
  The induced emf is ε = -dΦ/dt = NB₀πa²ω sin(ωt).
  The instantaneous power is P = ε²/R.  The mean power is <P> = (NB₀ πa²ω)²/(2R).
  (b)  The total field at the center the coil at the instant t is B_t = B₀ + B_i, where B_i is the magnetic field due to the induced current
  B_i = B_i(cos(ωt)i + sin(ωt)j) with  B_i = μ₀NI/(2a) and I = ε/R.
  [cos(ωt)i + sin(ωt)j is the direction of the vector surface S.]
  Therefore B_i = μ₀N²B₀πaω sin(ωt)/(2R).
  The mean values of its components are
  <B_ix> = [μ₀N²B₀πaω/(2R)]<sin(ωt) cos(ωt)> = 0,
  <B_iy> = [μ₀N²B₀πaω/(2R)]<sin²(ωt)> = μ₀N²B₀πaω/(4R)].
  For the total field we have
  <B_t> = B₀i +  μ₀N²B₀ πaω /(4R)]j.
  The needle orients along the mean field, therefore tanθ = μ₀N²πaω/(4R).
  Finally, the resistance of the coil measured by this procedure, in terms of is
  R = μ₀N²πaω/(4tanθ).

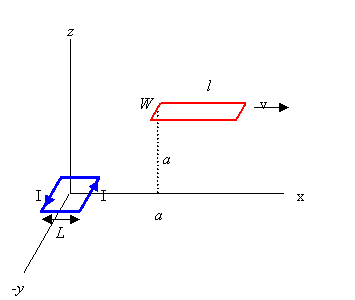
Problem:

A square loop of wire with sides of length L carries a time-independent current I and is located at the origin.  A rectangular loop of wire of length l and width W is moving parallel to the x-axis in the positive direction at a constant velocity v.  Its width is so small that the variation of the field along its width may be neglected.  At t = 0, the nearest edge of the rectangular loop has the coordinates (a,0,a), where a >> L.  Find the induced emf in the rectangular loop at t = 0. 

Solution:

• Concepts:
  Dipole moment, dipole field, induced emf
• Reasoning:
  The small current loop at the origin has a dipole moment, and its magnetic field is approximately a dipole field.  The rate of change of the flux of this field through the rectangular loop is proportional to the induced emf in the rectangular loop.
• Details of the calculation:
  Let us use Gaussian units.
  The dipole moment of the loop is m = k IA = k IL² = k m.
  The magnetic field produced by this loop at r (r >> L) is
  B = k_m(3(m∙r)r - mr²)/r⁵ =  k_m(3mzr - kmr²)/r⁵.  (k_m = μ₀/(4π))
  The induce emf is ε = -(∂F/∂t), with F = ∫_A(B∙k)dA.
  B∙k = k_m(3mz² - mr²)/r⁵ = k_mm(2z² - x²)/(x² + z²)^5/2.
  At t = 0  F = ∫_A(B∙k)dA = Wk_m ∫_a^a+ldx m(2a² - x²)/(a² + x²)^5/2
  After the loop has moved a small distance dx', the flux is
  F = Wk_m ∫_a+dx'^a+l+dx'dx m(2a² - x²)/(a² + x²)^5/2
  The change in flux therefore is
  ∂F/∂x' = -Wk_mm(2a² - a²)/(a² + a²)^5/2 + Wk_mm(2a² - (a + l)²)/(a² + (a + l)²)^5/2
  = Wk_mm[-1/(2^5/2a³) + a²(1- (l² + 2al)/a²)/(2a²(1 + (l² + 2al)/(2a²)))^5/2]
  = Wk_mm(1/(2^5/2a³))[-1 + (1 - (l² + 2al)/a²)/(1 + (l² + 2al)/(2a²))^5/2]
  ∂F/∂t = (∂F/∂x')(∂x'/∂t)
  = Wk_mmv(1/(2^5/2a³))[-1 + (1 - (l² + 2al)/a²)/(1 + (l² + 2al)/(2a²))^5/2]
  ε = -(∂F/∂t) = Wk_mmv(1/(2^5/2a³))[1 - (1 - (l² + 2al)/a²)/(1 + (l² + 2al)/(2a²))^5/2]