Faraday's law

Problem:

A small circular search coil is used to search for stray magnetic fields around a transformer.  The coil diameter is 1.5 cm and its output is connected to an ideal voltmeter.  For a stray field of 1 mT at 60 Hz, how many turns would be required for the search coil to produce a reading of 1 mV?

Solution:

• Concepts:
  Faraday's law
• Reasoning:
  The voltage in the coil is induced by a changing magnetic flux.  The magnetic flux changes with frequency f = 60 Hz.
• Details of the calculation:
  ε  = -∂F/∂t = induced emf, F = ∫_AB∙n dA, F ≈ BA = B₀e^iωtπR²N,  N = number of turns, when the face of the coil is perpendicular to the direction of the magnetic field.
  ∂F/∂t = iωB₀e^iωtπR²N = -ε = V = V₀e^i(ωt+φ).
  V₀ = ωB₀πR²N,  N = V₀/(ωB₀πR²) .
  V_rms = V₀/(√2) = 1 mV is the reading of the voltmeter.
  N =  √2*10^-3V/(2π*60 s^-1*10^-3 T*π(7.5 10^-3 m)²) = 21.

Problem:

(a)  A coil has an inductance of 2 mH, and a current through it changes from 0.2 A to 1.5 A in a time of 0.2 s.  Find the magnitude of the average induced emf in the coil during this time.
(b)  A 25 turn circular coil of wire has a diameter of 1 m.  It is placed with its axis along the direction of the Earth's magnetic field (magnitude 50 μT), and then, in 0.2 s, it is flipped 180^o.  What is the average emf generated?

Solution:

• Concepts:
  Faraday's law, induced emf
• Reasoning:
  The magnetic flux through a coil is changing and we are asked to find the induced emf.
• Details of the calculation:
  (a)  L = 2 mH,  dI/dt = (1.5 - 0.2) A/0.2 s = 6.5 A/s.
  ε = -LdI/dt = -(0.002 Vs/A)(6.5 A/s) = -0.013 V.
  The minus sign indicates that the induced emf opposes the flux changes that produced it.
  |ε| = 13 mV.
  (b)  ε = -dΦ/dt. Φ = NAB = 25π(0.5 m)²50*10^-6 T = 9.82*10^-4 Tm².
  dΦ/dt = 2(9.82*10^-4 Tm²)/(0.2 s) = 9.82*10^-3 V = 9.82 mV.
  (The flux does not just drop to zero, it changes sign.  This introduces the factor of 2.)

Problem:

Clever farmers whose lands are crossed by large power lines have been known to steal power by stringing wire near the power line and making use of the induced current.
Suppose that the farmer places a rectangular loop with two sides of length a parallel to the power line, the closest one at distance 5 m from it.  The loop and the power line lie in the same plane.  Let the length of the sides perpendicular to the power line be b = 0.5 m.  The power line carries a 60 Hz alternating current with a peak current of 10 kA.
(a)  If the farmer wants a peak voltage of 170 V (which is the peak of standard 120 V AC power) what should be the length a?
(b)  If the equipment the farmer connects to the loop has a resistance R = 5 Ω, what is the farmer's average power consumption?
(c)  If the power company charges 10 cents per kWh, what is the monetary value of the energy stolen each day?
(Give a numerical answer!)

Solution:

• Concepts:
  Faraday's law
• Reasoning:
  The magnetic flux through a loop is changing with time.  This flux change induces an emf.  The emf causes a current to flow, which dissipates energy.
• Details of the calculation:
  (a)  Ampere's law:  B = μ₀I/(2πr), B encircles the power line.
  Flux of B through the rectangular loop:  F = a[μ₀I/(2π)] ∫_5m^5.5mdr/r = a[μ₀I/(2π)]ln(5.5/5).
  emf = -dF/dt = -a[μ₀/(2π)](dI/dt)ln(5.5/5).
  Peak emf = a[μ₀/(2π)](2π*60/s*10⁴ A)ln(5.5/5) = a*0.072 V/m.
  For a peak emf of 170 V we need a = 2.37 km.
  (b)  P = V²_rms/R = (120 V)²/(5 Ω) = 2.88 kW.
  (c)  2.88 kW *24 h = 69.12 kWh.  The monetary value is $6.91 per day.

Problem:

A non-conducting ring of mass M, radius R, and total charge Q uniformly distributed around the ring hangs horizontally, suspended by non-conducting thin ("massless") strings as shown.

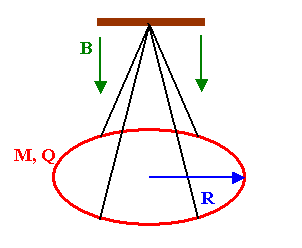
A uniformly increasing magnetic field B = B₀t pointing down is turned on at time t = 0.
(a)   Find the torque on the ring in terms of B₀, M, R, and Q.
(b)   If the strings supporting the ring provide a torque -αφ, where φ is the angle through which the ring turns, write the equation of motion in terms of B₀, M, R, Q and α.

Solution:

• Concepts:
  Faraday's law
• Reasoning:
  A changing magnetic flux through a ring induces an emf.  The resulting electric field exerts a force on the charge Q on the ring.  This force produces a torque about the center of the ring.
• Details of the calculation:
  (a)  The emf induced in the ring is  
  ∮_Γ E∙dr = -∂/∂t∫_AB∙n dA = -πR²∂B/∂t = -πR²B₀.
  The magnitude of the induced electric field is therefore given by
  2πRE = πR²B₀, E = RB₀/2.
  The direction of E is tangential, counterclockwise for increasing B.
  The torque on the ring τ = QRE = QR²B₀/2 in the vertical direction.
  (b)  Total torque τ_total = Id²φ/dt² = MR² d²φ/dt² = QR²B₀/2 - αφ, where we measure φ ccw from the equilibrium position.
  Equation of motion:  d²φ/dt² = QB₀/(2M) - αφ/( MR²).
  Resulting motion:
  Harmonic oscillation about a position φ₀ = QR²B₀/(2α) with angular frequency ω = (α/( MR²))^½.

Problem:

An electron accelerator employs a time varying magnetic flux through a plane circular loop of radius R = 0.85 m, and the electrons always move in this circular path with this radius.  The magnetic induction in the loop plane

B(r) = B₀ - Kr²,  r < R;    B = 0, r > R,

is everywhere normal to the loop plane with r the distance from the loop center.
(a)  Show that, at any instant, the average magnetic induction in the loop B_av, must be related to B_R by B_av = 2B_R.  Evaluate K.
(b)  B₀ increases linearly from 0 to 1.2 Tesla in 5.3 sec.  Deduce the energy gain per turn for the electrons and the maximum electron energy achieved.

Solution:

• Concepts:
  Faraday's law, induced emf, motion in a circular orbit at relativistic speeds
• Reasoning:
  The changing magnetic flux through a circular loop induces an emf.  The resulting electric field is tangential to the loop and accelerates the electron.  A light electron soon reaches relativistic speed.
• Details of the calculation:
  (a)  You can show part (a) using relativistic or non-relativistic equations.
  For an electron in a circular orbit lying in the x-y plane perpendicular to the magnetic field B = Bk and centered at the origin we have
  F = -q_ev × B(R) = -q_evB(R)(r/r) (SI units).
  For a particle in a circular orbit the centripetal force is F = -(γmv²/R)(r/r).
  
  [Assume a particle moving in a circular orbit of radius r with constant speed v.
  x = rsinωt,  y = -rcosωt,
  v_x = ωrcosωt,  v_y = ωrsinωt,
  p_x = γmωrcosωt,  p_y = γmωrsinωt,
  F_x = dp_x/dt = -γmω²rcosωt = -γmω²x,  F_y = dp_y/dt = γmω²rcosωt = -γmω²y.
  F = -γmω²r = -(γmv²/r²)r.]
  We therefore have q_evB(R) = γmv²/R = pv/R,  B(R) = p/(q_eR).
  |ε|  = |∂F/∂t| is the magnitude of the induced emf.  Assume B is increasing with time.
  2πRE = ∂(B_avgπR²)/∂t,  E = (R/2)dB_avg/dt.
  The magnitude of the tangential force accelerating the electron is
  F_t = q_eE = (q_eR/2)dB_avg/dt.
  So we have dp/dt = (q_eR/2)dB_avg/dt, and  dp/dt = (q_eR)dB(R)/dt.
  ½dB_avg/dt = dB(R)/dt, ΔB_avg/2 = ΔB(R).
  If we start with B = 0 we have  B_avg = 2B(R).
  B(r) = B₀ - Kr²,  r < R,    πR²B_avg = 2π∫(B₀ - Kr²)rdr with integration limits 0 and R.
  B_avg = B₀ - KR²/2,  B(R) = B₀ - KR², B₀ - KR²/2 = 2(B₀ - KR²),
  B₀ = (3/2)KR², K = (2/3)B₀/R².
  B(r) = B₀(1 - (2/3)r²/R²).
  (b)  |ε|  = ∂(B_avgπR²)/∂t = (2πR²/3)dB₀/dt = energy gain per unit charge per revolution.
  q_e|ε|  = energy gain of an electron per revolution.
  dB₀/dt = (1.2 T)/(5.3 s),  q_e|ε| = 5.48*10^-20 J.
  To find the total energy gained we note:
  F = dp/dt = q_eE = constant.  p = q_eEt.  Energy = (p²c² + m²c⁴)^½.
  E = (R/2)dB_avg/dt = (2/3)(R/2)dB₀/dt = (R/3)dB₀/dt.
  p = q_e(R/3)(1.2 T/5.3 s)t.  After 5.3 s p = q_e(R/3)1.2 T = 5.44*10^-20 kgm/s.
  Energy = ((5.44*10^-20 kgm/s)²c² *(1 MeV/1.6*10^-13 J)² + (0.511 MeV )²)^½ = 102 MeV.
  Energy gained:  102 MeV - 0.511 MeV.

Problem:

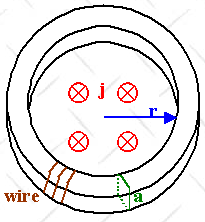
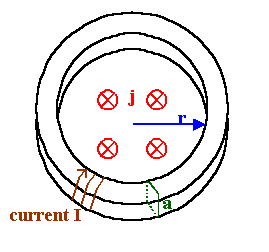
A spatially uniform current density j = j₀ cosωt flows through the hole of a torus along the axis of the torus as shown.  The inner radius of the torus is r, and the cross section is square with sides a (a << r).  The torus is made of an insulating material with m = μ₀.  A wire of resistance R wraps around the torus with a total of N turns.  Determine the current flowing in the wire.

Solution:

• Concepts:
  Ampere's law, Faraday's law
• Reasoning:
  Amperes law, ∮_Γ B∙ds =  μI_{through_Γ}  yields B inside the torus.  Since the flux of B through the wire loops surrounding the torus is changing, an emf is induced in the wire loops and a current flows.
  Assume R is large and neglect the self-inductance of the loops.
• Details of the calculation:
  B inside the torus is tangential (clockwise for j pointing into the paper),
  2πrB(r) = μ₀ j₀ cosωt πr², 
  B(r) = μ₀ j₀ cosωt r/2. 
  Since a << r, we assume that B is approximately constant inside the torus.
  (Note: r here is not a variable, but the radius of the torus.)
  The flux of B through one loop of the wire is B(r)a².  The total flux through the N loops is NB(r)a².
  The emf induced in the wire is
  ∮_Γ E∙dr = -∂/∂t∫_AB∙n dA = -Na²∂B/∂t.
  We have V = Na² μ₀ ω j₀ sinωt r/2.
  I = V/R = Na² μ₀ ω j₀ sinωt r/(2R).
  

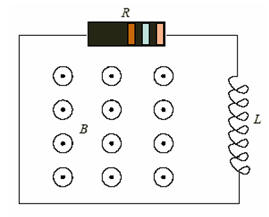
Problem:

A loop of wire of resistance R and a coil of self-inductance L encloses an area A.  A spatially uniform magnetic field is applied perpendicular to the plane of the loop with the following time dependence:
For t < 0 the field is zero, for 0 < t < t₀ B(t) = kt, for t > t₀  the field remains constant at B₀ = kt₀. 
(a)  Calculate the current I in the loop for all times t > 0, given that I = 0 for t = 0. 
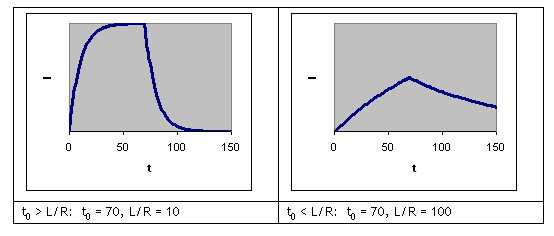
(b)  Make simple sketches of the current vs.  time for t₀ < L/R and t₀ > L/R..

Solution:

• Concepts:
  Faraday's law, Lentz's rule
• Reasoning:
  The magnetic flux through a filamentary loop is changing with time.  This flux change induces an emf.
• Details of the calculation:
  (a)  Flux Φ = BA = ktA for t < t₀,  Φ = BA = kt₀A for t > t₀.
  emf = -dΦ/dt = -kA for t < t₀,  Φ = BA = 0 for t > t₀.
  The resulting current flows in the clockwise direction.
  For t < t₀:  IR + LdI/dt = kA,  dI/dt = kA/L - IR/L,
  Try I = a - bexp(-ct),  Then a = kA/R, c = R/L,  I = 0 at t = 0 yields b = kA/R,
  I(t) = (kA/R)(1 - exp(-Rt/L)).
  For t > t₀:  dI/dt = -IR/L,  I(t) = I(t₀)exp(-R(t - t₀)/L)
  (b) 

  

Problem:

A square loop with side b is made of a wire of mass m and negligible electric resistance. The loop has a gap which can be closed with a switch.  Initially the switch is open.  The loop is pivoted along its top horizontal side and placed in the weak vertical uniform magnetic field B as shown.  The loop is then pulled to a horizontal position, the switch is closed and the loop is released. Eventually, the loop comes to rest due to air resistance. Find the angle θ that the plane of the loop makes with the vertical at the final position. The self inductance of the loop is L.

Solution:

• Concepts:
  Induced emf, quasi-static situations
• Reasoning:
  The wire has no resistance.  The flux of B through the loop is constant.  Any change in the flux of the external field through the loop is immediately canceled by the change in the flux F = LI due to a induced current in the loop. 
  We therefore have Bb² = Bb²sinθ + LI.
  (initial flux = final flux)
• Details of the calculation:
  In equilibrium the gravitational torque must cancel the torque on the current loop in the magnetic field.
  Magnitude of gravitational torque about pivot line: 
  (m/4)g b sinθ + 2(m/4)g (b/2) sinθ = ½ b mg sinθ.
  Magnitude of magnetic torque about pivot line:
  Ib²B cosθ.
  We need:
  ½ b mg sinθ = Ib²B cosθ.
  We have two equations for two unknowns, I and θ,
  I = (Bb²/L)(1 - sinθ)  and tanθ = 2IbB/(mg).
  Combining these equations we obtain
  tanθ = C(1 - sinθ),  with C = 2b³B²/(mgL).
  Since the field is weak, θ << 1, tanθ ~ sinθ ~ θ,  θ  = C(1 - θ),  θ = C/(1 + C).