Mutual and self inductance

Problem:

You need 12 V to run an electric train, but the outlet voltage is 120 V.  What is the ratio of the number of turns on the primary coil to the number of turns on the secondary coil of the transformer you are using?

Solution:

• Concepts:
  Mutual inductance, self inductance, the transformer
• Reasoning:
  A prototype of a transformer has a primary and a secondary coils wound on either side of an iron ring.  If the current in the primary coil is changing, the flux through the secondary coil changes and an emf is induced in the secondary coil. The emf induced in the secondary coil is proportional to the number of turns N₂ of the secondary coil, since the number of turns determines the total magnetic flux passing through this coil.  The induced emf is also proportional to the voltage V₁ across the primary coil, since this determines the magnitude of the primary current and its associated magnetic field.  The induced voltage is inversely proportional, however, to the number of turns N₁ of the primary coil.  The relationship takes the form

  V₂/N₂ = V₁/N₁.

  The ratio of the number of turns on the two coils determines the ratio of the voltages.  Self-inductance is the reason that the emf induced in the secondary coil is inversely proportional to the number of turns of the primary coil.  If the primary coil has more turns, it is harder to produce a rapid change in current flowing through it, because of the back emf produced by self-induction.  This effect limits the current and therefore the magnitude of the magnetic field produced by the primary coil, which in turn limits the magnetic flux passing through the secondary coil.
  
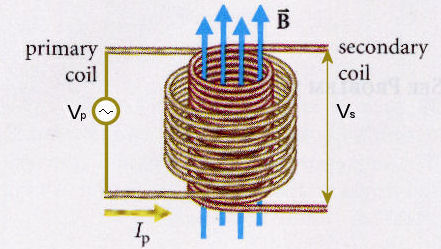
  Assume the same field B is penetrates both coils and the flux per turn Φ_B is the same for both coils.  The total flux per turn is due to the currents in both coils.  In a well designed transformer, the resistance of the coils is small, and we neglect it here.  Then the induced emf in the primary coil must exactly balance the applied voltage V_p.
  V_p = N₁dΦ_B/dt.
  Since Φ_B is the same for the secondary coil, the induced emf in the secondary coil is ε_s = N₂dΦ_B/dt.  As long as no load is connected, we measure an output voltage V_s =  N₂dΦ_B/dt.
  V_p/N_p = V_s/N_s.

• Details of the calculation:
  N₁/N₂ = V₁/V₂.  You need a transformer with ten times as many turns on the primary coil as on the secondary coil.

Problem:

A large coil of radius a is lying in the x-y plane, centered at the origin.   A coaxial small coil of radius b << a with its axis parallel to the z-axis lies at a distance z above the large coil.  The small coil carries a steady current I.
(a)  Find the magnetic flux coupled into the large coil.
(b)  If the small coil moves along the z-axis at constant velocity v = v₀k, what is the emf ε induced in the large coil as a function of time?  Let z = 0 at t = 0.

Solution:

• Concepts:
  Flux  F = ∫_AB∙n dA,  F = MI,  M = mutual inductance, ε  = -∂F/∂t = induced emf
• Reasoning:
  After finding the mutual inductance of the coils as a function of coil separation, we can find the flux through the large coil and the induced emf.
• Details of the calculation:
  (a)  The flux through the large coil due to a current I in the small coil is F = MI.  To find M, we calculate the flux through the small coil due to a current I in the large coil.
  [When calculating the mutual inductance, you can calculate the flux through circuit 1 due to a current in circuit 2 or the flux through circuit 2 due to a current in circuit 1.  In a given problem, one of these calculations is often much simpler than the other.]
  The field on the axis of a current loop of radius a is B = k μ₀Ia²/[2(a² + z²)^3/2] (SI units), if the current flows in the φ direction. 
  The flux through the loop of radius b is   F = ∫_AB∙n dA.
  F = πb² μ₀Ia²/[2(a² + z²)^3/2].  (Since b << a, B is nearly constant over the area if the small loop.)
  F = MI,  M = πb²a²μ₀/[2(a² + z²)^3/2].
  (b)  ε  = -∂F/∂t = -(πb²a²μ₀I/2)(∂/∂t)(1/(a² + z²)^3/2)
  = (3πb²a²μ₀I/4)(1/(a² + z²)^5/2)2zv₀.
  ε  = (3πb²a²μ₀I/2)(zv₀/(a² + z²)^5/2).

Problem:

A toroidal coil of N turns has a square cross section, each side of the square being of length a, and inner radius b.
(a)  Find the self-inductance of the coil.
(b)  Find the mutual inductance of the system consisting of the coil and a long, straight wire along the axis of symmetry of the coil.  (Assume that the conductors closing the circuit of which the long straight wire is part of are located far from the coil, so that their influence may be neglected.)
(c)  Find the ratio of the self-inductance of the coil to the mutual inductance of the system.

Solution:

• Concepts:
  Ampere's law, magnetic flux, mutual inductance, self inductance
• Reasoning
  Ampere's law can be used to find the magnetic fields due to the coil and due to the wire.  By finding the flux of these fields through the coil we can find the self inductance and the mutual inductance.
• Details of the calculation:
  (a) Amperes law yields the magnetic field inside the torus due to a current I in the windings.  Symmetry dictates that the magnetic field points into the (φ/φ)-direction.
  B = (φ/φ) μ₀NI/(2πr).  Here N is the number of turns of the windings.
  
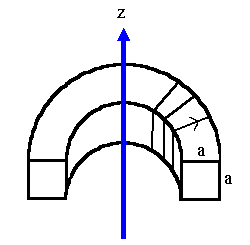
  The flux of this field through the windings is
  F = ∫ B∙dA  = [μ₀N²I/(2π)]a∫_b^b+a(1/r)dr = [μ₀N²I/(2π)]a ln((b+a)/b).
  F = LI,  L = [μ₀N²a/(2π)] ln((b+a)/b).
  (b)  Amperes law yields the magnetic field inside the torus due to a current I in the wire.
  B = (φ/φ)μ₀I/(2πr).
  The flux of this field through the windings is
  F = ∫ B∙dA  = [μ₀NI/(2π)]a∫_b^b+a(1/r)dr = [μ₀NI/(2π)]a ln((b+a)/b).
  F = MI, M = [μ₀Na/(2π)] ln((b+a)/b).
  (c)  L/M = N.

Problem:

A long cable carries current in one direction uniformly distributed over its circular cross section.  The current returns along the surface (there is a very thin insulating sheath separating the currents).  Find the self inductance per unit length.

Solution:

• Concepts:
  Self inductance, Ampere's law, U = ½LI² = (1/(2μ₀))∫ B²dV.
• Reasoning:
  We find the magnetic field produce by the current from Ampere's law and solve
  ½LI² = (1/(2μ₀))∫ B²dV for the self inductance L.
• Details of the calculation:
  Assume the wire has radius a and is concentric with the z-axis.  Assume it carries a current I.
  For a circular loop Γ of radius r, concentric with the z-axis and lying in the x-y plane  we have
  2πrB = μ₀I_{through Γ}. 
  B = B (φ/φ).
  I_{through Γ} = Ir²/a².
  r < a:  B = μ₀Ir/(2πa²)
  r > a:  B = 0.
  For a section of unit length we have
  (½μ₀)∫ B²dV = (π/μ₀)( μ₀I/(2πa²))²∫₀^ar³dr = (π/μ₀)(μ₀I/(2πa²))²(a⁴/4)
  = (μ₀I²/(16π)) = ½LI².
  L = (μ₀/(8π)).

Problem:

A superconducting loop of radius R has self inductance L.  A uniform and constant magnetic field B is applied perpendicular to the plane of the loop.  Initially, current in this loop is zero.  The loop is rotated by 180^o.  Find the current in the loop after the rotation.

Solution:

• Concepts:
  Motional emf
• Reasoning:
  The loop has no resistance.  The motional emf must be canceled by the induced emf due to the self inductance of the loop.
• Details of the calculation:
  Motional emf = -dF/dt,  F = flux= BA cosθ. 
  As the loop is rotated, the magnitude of the flux changes from B πR to -B πR
  LdI/dt = -dF/dt,  LI = 2πR²B.  I = 2πR²B/L.