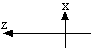Motional emf

Problem:

Solution:

• Concepts:
  Motional emf
• Reasoning:
  The emf is generated by sliding the conducting rod in a direction perpendicular to the magnetic field
• Details of the calculation:
  The emf driving the current is equal to vBd where d is the length of the section of wire connecting the rails. (The work done per unit charge (voltage) is vBd, when a charge moves from one end of the moving wire to the other end.)  The current flowing in the circuit will be I = vBd/R, where R is the resistance of the circuit.
  Therefore v = IR/Bd = 0.5 A*6 Ω/(2.5 T*1.2 m) = 1 m/s.

Problem:

A pair of parallel conducting rails a distance d apart is placed in a uniform magnetic field B which is perpendicular to the rails.  A resistance R is connected across the rails and a conducting bar of mass m and negligible resistance is placed at rest on the rails and perpendicular to them.  A constant force F is applied to the bar pulling it along the rails.
(a)  What is the value of v when the bar's acceleration becomes zero?
(b)  Derive an expression for the speed v(t) of the bar as a function of time.
(c)  If F is suddenly reduced to zero at time t' = ln(2) mR/(Bd)², find the rate of decrease of the kinetic energy of the bar for t > t'.
(d)  Show that the rate of decrease of the kinetic energy of the bar is equal to the ohmic heating rate.

Solution:

• Concepts:
  Motional emf,  Newton's second law
• Reasoning:
  The motional emf causes a current to flow.  The magnetic force on this current points into the opposite direction of the velocity of the bar.
• Details of the calculation:
  (a)  Current in the circuit:  I = ε/R, ε = Bd(dx/dt) = Bdv.
  Net force on the rod and mass: F_net = F - IdB.
  Constant speed:  F_net = 0, F = IdB = (Bd)²v/R,  v =  FR/(Bd)².
  (b)  m(d²x/dt²) = F - (Bd)²(dx/dt)/R,  dv/dt = F/m - [(Bd)²/(mR)]v.
  Let v = v₀(1 - exp(-t/τ)), then dv/dt = (v₀/t) exp(-t/τ) = -v/τ + v₀/τ.
  τ = mR/(Bd)²,  v₀/τ = F/m, v₀ = FR/(Bd)².
  v = [FR/(Bd)²] [1 - exp(-(Bd)²t/ (mR))].
  (c)  At t = ln(2) mR/(Bd)² = ln(2) τ, v = v₀/2 = ½ FR/(Bd)².
  When F = 0, dv/dt =  -[(Bd)²/(mR)]v = -v/ τ.
  For t > t', v(t) = (v₀/2)exp(-(t-t')/τ),  T = ½mv² = (mv₀²/8) exp(-2(t-t')/τ),
  dT/dt = -(mv₀²/(4τ)) exp(-2(t-t')/τ).
  (d)  The rate of ohmic heating is P = ε²/R.
  P = (Bdv)²/R = ((Bd)²/R](v₀²/4) exp(-2(t-t')/τ) = (mv₀²/(4τ)) exp(-2(t-t')/τ),  using τ = mR/(Bd)². 

Problem:

Two identical conducting bars rest on two horizontal parallel conducting rails.  The bars are perpendicular to the rails and parallel to each other as shown.  The distance between the bars is L.  At a certain moment, a uniform vertical upward magnetic field is turned on.  The field quickly reaches its maximum magnitude and then remains constant.
Neglecting friction, find the new distance between the bars.  Assume that the resistance of each bar is much greater than the resistance of the rails.

Solution:

• Concepts:
  Quasi-static approximation
• Reasoning:
  We neglect radiation in this problem.
• Details of the calculation:
  The magnetic field in the z-direction increases from 0 to B in a small time interval Δt.
  Δt --> 0, so the displacement of the rods ±Δx --> 0 during this time interval.
  During the time interval Δt the emf in the circuit is
  |ε| = (∂B/∂t)LW = (B/Δt)LW as Δt --> 0.
  During the time interval Δt a current I = |ε|/(2R) flows clockwise in the circuit.  Here R is the resistance of each rod.
  The bar in the right experiences a force F(t) = IWB(t) in the negative x-direction.  The magnitude of the average force during he time interval Δt is F_avg = IWB/2 = W²B²L/(4RΔt), if the magnetic field increases linearly.  This force is responsible for a impulse of magnitude F_avgΔt.  After the time interval Δt the bar on the right will have momentum p = W²B²L/(4R) in the negative x-direction and the bar on the left will have momentum of the same magnitude in the positive x-direction.
  Set t = 0 when the magnetic field has reached its maximum magnitude.  At t = 0 the bars approach each other each with speed v = v₀ = W²B²L/(4RM), where M is the mass of each bar.
  If the bars move in a magnetic field with speed v, the motional emf generated in the circuit is |ε| = dF/dt, where F is the flux through the circuit. 
  |ε| = dF/dt = 2BWv.

  (We can also argue that each electron in the bars experiences a force of magnitude F = q_evB.  The work done on an electron by this force in moving it once around the circuit is F2W = q_evB2W, and the emf is the work per unit charge, |ε| = 2BWv.)
  The emf results in a current I = |ε|/(2R) = BWv/R, flowing counterclockwise in the circuit.  The magnitude of the force on each bar therefore is F = IWB = B²W²v/R, opposite to the direction of its motion.
  F = -Mdv/dt,  dv/dt = -B²W²v/(MR).
  This differential equation has the solution v = v₀exp(t/τ), where 1/τ = B²W²/(MR).
  The total distance traveled by each bar therefore is x = v₀∫₀^∞exp(t/τ)dt = v₀τ.
  x = [W²B²L/(4RM)][MR/(B²W²)] = L/4.
  The final distance between the bars is L/2.

Problem:

Under the influence of the gravity near the surface of the earth a square wire of length l, mass m and resistance R slides without friction down very long parallel conducting rails of negligible resistance.  The rails are connected to each other at the bottom by a rail of negligible resistance, parallel to the wire, so that the wire and the rails form a closed rectangular conducting loop.  The plane of the rails makes an angle θ with the horizontal, and a uniform vertical magnetic field B exists throughout the region.
(a)  Show that the wire acquires a steady state speed for any fixed θ.
(b)  If the angle θ is lowered from θ₁ = π/3 to θ₂ = π/6, find the percent change of the steady-state speed of the wire.
(c)  Find the percent change of the corresponding power converted into joule energy.

Solution:

• Concepts:
  Motional emf
• Reasoning:
  The square wire moves in a constant magnetic field.  The filamentary circuit changes shape.
• Details of the calculation:
  For a well-defined filamentary circuit which can change its shape we may write
  ε = -d/dt∫B∙dA.
  i.e. we can combine the emf due to flux changes and the emf due to shape changes into one equation.
  (a)  The wire and the rails form a circuit.  The flux through this circuit if F = BAcosθ.  A is the area of the circuit.
  Let us use SI units.  Then ε = -dF/dt, = -(Bcosθ l)(ds/dt) = -Bcosθ lv.  Here l is the length of the wire.
  I = |ε|/R.
  I = Bcosθ lv/R, the current flows counterclockwise when looking from above for a wire moving down the rail.
  The component of the Lorentz force on the rod in the direction opposite to the velocity is F_L = I l Bcosθ  = B²l²vcos²θ/R.
  The gravitational force is mgsinθ in the direction of the velocity, for a wire sliding down the rail.
  F_tot =-B²l²vcos²θ/R + mgsinθ.
  F_tot = mdv/dt.
  For dv/dt = 0 we need  B²l²vcos²θ/R = mgsinθ, v = R m g tanθ/(B²l²cosθ).
  (b)  v(π/3)/v(π/6) = tan(π/3)cos(π/6)/(tan(π/6)cos(π/3) = 5.2
  (v(π/3) - v(π/6))/v(π/3) = 0.8
  Percentage change: 80%
  (c)  Once the wire moves with constant speed, the rate at which gravitational potential energy is converted into thermal energy is P = mgdh/dt = mgvsinθ.
  P ∝ tan²θ.
  (P(π/3) - P(π/6))/P(π/3) = 0.89
  Percentage change: 89%

Problem:

A rod of length L, lying in the xy-plane, pivots with constant angular velocity ω counterclockwise about the origin.  A constant magnetic field of magnitude B₀ is oriented in the z-direction.  Find the motional emf in the rod.

Solution:

• Concepts:
  Motional emf
• Reasoning:
  The conducting rod is moving in a plane perpendicular to B.
• Details of the calculation:
  Speed of the rod as a function of the distance r from the origin: v(r) = ωr.
  Force on an electron: F_e = q_evB = q_eBωr. 
  Work done per unit charge: emf = Bω∫₀^Lrdr = BωL²/2.

Problem:

One end of a conducting rod rotates with constant angular velocity ω in a circle of radius r making contact with a horizontal, conducting ring of the same radius.  The other end of the rod is fixed.  Stationary conducting wires connect the fixed end of the rod (A) and a fixed point on the ring (B) to either end of a resistance R.  A uniform vertical magnetic field B passes through the ring.

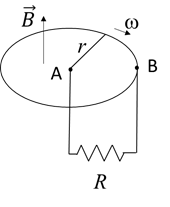
(a)  Find the emf produced in the system and its time dependence.   [Hint: find Lorentz force acting on the charges in the moving rod].
(b)  Determine direction of current flows in the circuit.
(c)  Determine work needed to rotate the rod for one full turn.

Solution:

• Concepts:
  Motional emf
• Reasoning:
  The conducting rod is moving in a plane perpendicular to B.
• Details of the calculation:
  (a)  Speed of the rod as a function of the distance r' from the origin: v(r') = ωr'.
  Force on an electron: F_e = q_evB = q_eBωr'.
  Work done per unit charge: emf = Bω∫₀^rr'dr' = Bωr²/2.
  The emf does not depend on time.
  (b)  The direction of the force on an electron is outward.
  The current flows from the ring through the rod towards the center.
  (c)  Assume that the resistance of the conducting rod and the wires is negligible.
  I = emf/R = Bωr²/(2R) is the current flowing through the resistor.
  P_e = I²R = B²ω²r⁴/(4R) is the rate heat is generated.
  W = P_eT = P_e2π/ω = πB²ωr⁴/(2R) is the work needed to rotate the rod for one full turn.

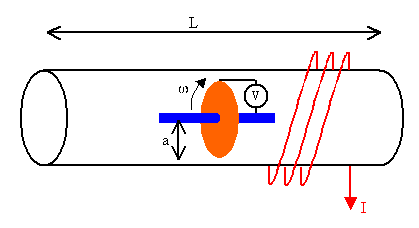
Problem:

(a)  A long solenoid of length L is wound with N turns of wire that carry a current I.  A copper disk of radius a rotates with angular velocity ω about a shaft at the center of the solenoid as shown in the figure below.  What is the potential difference between slip rings on the shaft and on the edge of the disk?
(b)  Assume L = 1 m, a = 10 cm, N = 1000, I = 2 A and the disk rotates 1200 revolutions per minute.  Calculate the potential difference in Volts.

Solution:

• Concepts:
  Motional emf
• Reasoning:
  Electrons in the disk are moving in circular orbits in a plane perpendicular to the magnetic field inside the solenoid.
• Details of the calculation:
  (a)  Use the orientation of the coordinate axes as shown below.
  
  The magnetic field inside the solenoid is B = μ₀I(N/L)k = Bk.
  An electron a distance ρ from the center of the disk is moving with velocity
  v = -ρω (φ/φ) and feels a magnetic force F_m = -q_ev × B = q_eρωB (ρ/ρ). 
  In equilibrium this force is balanced by an electric force F_e = -F_m.
  We therefore have a difference in electrostatic potential energy of the electron
  ΔU = U_rim - U_center = -∫₀^aF_e∙dr = ∫₀^aF_edr
  ΔU = ∫₀^aq_eρωBdρ = q_ea²ωB/2.
  ΔV = V_rim - V_center = ΔU/(-q_e) = -a²ωB/2 = -a²ωμ₀I(N/2L)
  (b)  ΔV = -(0.1 m)² 2π (1200/(60 s)) (1000/(2 m)) 2A (4*10^-7 N/A²) = -1.58*10^-3 V.
  The rim is at a lower potential than the center.

Problem:

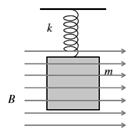
(a)  A thin copper plate of mass m has a shape of a square with a side b and thickness d.  The plate is suspended on a vertical spring with a force constant k in a uniform horizontal magnetic field B parallel to the plane of the plate.  Find the period of the small-amplitude vertical oscillations of the plate. 
Neglect the resistivity of the plate.

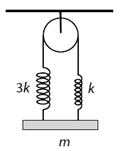
(b)  A bar of mass m is suspended horizontally on two vertical springs with the force constants k and 3k.  The bar bounces up and down while remaining horizontal.  Find the period of oscillations of the bar.  Neglect the mass of the string that connects the springs and the friction between the string and the pulley.

Solution:

• Concepts:
  Small oscillations, motional emf
• Reasoning:
  (a)  In addition to energy being stored in the spring, there is also energy stored in the separated charge on the plate.
  (b)  Since the bar remains horizontal at all times, the forces exerted by each of the springs always have equal magnitudes. 
• Details of the calculation:
  (a)  Consider the plate at an instant that it is moving vertically downward with velocity v.  The motional emf (Hall voltage) produced is ε = Bvd.
  The front square face of the plate will become positively charged, and the back face will have a negative surface charge density of equal magnitude and opposite sign.  We thus have a parallel-plate capacitor with capacitance C = ε₀b²/d.
  The energy stored in this capacitor is U_E = ½Cε² = ½ε₀b²B²v²d.
  Let the y-axis point downward.
  dU_E = -F_Eydy,  F_Ey = -dU_E/dy = -ε₀b²B²d (v dv/dy) = -ε₀b²B²d (v dv/dt dt/dy) = -ε₀b²B²d a.
  Newton's second law:  ma = -ε₀b²B²d a - ky.
  (m + ε₀b²B²d) d²y/dt² = -ky.
  y = y₀cos(ωt + φ) ,  ω² = k/((m + ε₀b²B²d).
  T = 2π/ω = 2π[(m + ε₀b²B²d)/k]^½.
  
  (b)  Assume that the bar has an instantaneous displacement y below its equilibrium position.  The total elongation of both springs together is then 2y.  If the individual springs are stretched by y₁ and y₂ then y₁ + y ₂ = 2y.
  We have y₁ = F/(3k) and y₂ = F/k, so y₂ = 3y₁ and y₁ = ½ y,  y₂ = (3/2 )y.
  The effective spring constant is k_eff = 2F/y = 2ky₂/y = 3k.
  The period of oscillation therefore is T = 2π/ω = 2π[(m/(3k)]^½.