Other AC circuits

Problem:

(a)  Show that in an AC circuit (V = Re(V₀exp(iωt)) with resistive and reactive circuit elements the average power dissipated is P_avg = ½Re(VI*) = I²_rmsR.
(b)  Calculate the average power dissipated by a 25 Ω resistor, when powered by a square-wave with a symmetrical amplitude of 100 volts and a frequency of 2 kHz:

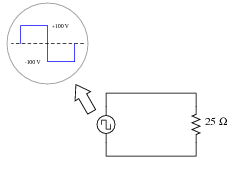
Solution:

• Concepts:
  AC circuits
• Reasoning:
  We have to average the instantaneous power over one cycle.
• Details of the calculation:
  (a) I =  Re(I₀exp(i(ωt + φ)) =  I₀cos(ωt + φ)
  V = Re(IZ) = Re(I(R + iX)) = I₀Rcos(ωt + φ) - I²₀Xsin(ωt + φ)
  Instantaneous power:  P = IV = I₀²Rcos²(ωt + φ) - I₀²Xsin(ωt + φ)cos(ωt + φ)
  Averaged over one cycle, <cos²(ωt)> = ½, <cos(ωt)sin(ωt> = 0.
  Therefore P_avg = ½I₀²R = I²_rmsR.
  There is no energy loss in the reactive part.
  In complex notation: VI* = I₀²(R + iX)), ½Re(VI*) = ½I₀²R = I²_rmsR.
  (b)  There is no reactance in the circuit.  P(t) = I(t)V(t) = I²(t)R = 400 W
  P_avg = I²_rmsR = V²_rms/R = 400 W  (The formula still works.)

Problem:

A heavy block is attached to the ceiling by a spring that has a force constant k.  A conducting rod is attached to the block.  The combined mass of the block and the rod is m.  The rod can slide without friction along two vertical parallel rails, which are a distance l apart.  A capacitor of known capacitance C is attached to the rails by the wires.  The entire system is placed in a uniform magnetic field B directed as shown.  Find the period T of the vertical oscillations of the block.  Neglect the electrical resistance of the rod and all wires.

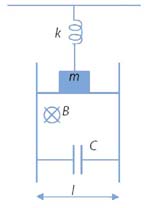
Solution:

• Concepts:
  Motional emf, AC circuits
• Reasoning:
  If the block oscillates with angular frequency ω, then the motional emf induced in the circuit has angular frequency ω.  Since the circuit has no resistance the sum of the motional emf and the voltage across the capacitor must be zero.  The capacitor must charge and discharge appropriately and we can find the current flowing in the AC circuit.  Given the current, we can find the total force on the rod.
• Details of the calculation:
  We neglect the self inductance of the circuit.
  Let the z-axis be the vertical axis, let z = 0 denote the equilibrium position of the rod, and let the upward direction be the positive z-direction.
  Assume the mass is oscillating with angular frequency ω.
  Let z = z₀exp(iωt).  [The real part of the equation describes the motion.]
  Then v = iωz₀exp(iωt).  [z and v are 90^o out of phase.]
  The motional emf is ε = vBl = iωz₀Blexp(iωt).  [The emf and v are in phase.]
  When the mass moves through its equilibrium position into the positive z-direction, v and the emf have their maximum values, the left plate of the capacitor is positively charged.
  As z increases, v and the emf decrease, and a current flows from left to right through the rod as the capacitor discharges.
  I = ε/Z_C,  Z_C = 1/(iωC) is the impedance of the capacitor.
  I = -ω²z₀BlCexp(iωt).
  The force on the wire therefore is F = IlB in the upward direction.
  F = ω²z₀B²l²Cexp(iωt) = ω²B²l²Cz.
  The force due to the spring is F = -kz, so F_total = -(k - ω²B²l²C)z = -k'z,
  ω = (k'/m)^½ = [(k - ω²B²l²C)/m]^½.  ω² = (k - ω²B²l²C)/m.  (1 + B²l²C/m)ω²  =  k/m.
  ω²  =  k/[m + B²l²C].  T = 2π/ω = 2π/[k/[m + B²l²C]]^½ = 2π[m + B²l²C]^½/k^½.