RC circuits (AC)

Problem:

For the RC circuit shown on the picture, calculate the U₂, knowing the sinusoidal change of U₁.

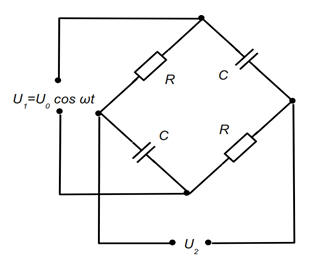
Solution:

• Concepts:
  AC circuits
• Reasoning:
  The circuit shown is a simple, two terminal, AC circuit.
• Details of the calculation:
  The impedance of the capacitor is Z_C = -i/(ωC) = -iX and the impedance of the resistor is Z_R = R.
  In each branch  of the circuit (left and right) I = U₁/(Z_C + Z_R).
  U₂ = IZ_R - IZ_C = U₁(Z_R - Z_C)/(Z_R + Z_C) = U₁(R + iX)/(R - iX) = U₁e^iφ.
  tan(φ/2) = X/R = 1/(ωRC).
  U₂ = Re(U₁exp(iφ)).
  U₂ = U₀cos(ωt + φ).
  The voltage amplitude stays the same, the phase is shifted.

Problem:

In electronic circuits it is often desired to provide a sinusoidal voltage of constant amplitude but variable phase.  A circuit which accomplishes this is called a phase shifting network.  One example of such a network is shown in the figure.  Show that the voltage measured between terminals A and B has half the amplitude of the input voltage, and a phase which may be adjusted between 0^o and 180^o by changing the resistance R'.

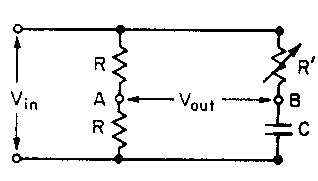
Solution:

• Concepts:
  AC circuits
• Reasoning:
  We have a two-terminal network and a AC generator, generating a sinusoidal voltage.
• Details of the calculation:
  V_in = I₁Z₁ = I₂Z₂.  Z₁ and Z₂ are in parallel.
  Z₁ = 2R,  Z₂ = R' + 1/(iωC) = R' - i/(ωC).
  V_in = V₀exp(iωt),  I₁ = (V₀/2R)exp(iωt),  I₂ = (V₀/(R' - i/(ωC)))exp(iωt).
  V_A = V_in - I₁R,  V_B = V_in - I₂R'.
  V_out = V_A - V_B = -I₁R + I₂R'.
  V_out = [V₀R'/(R' - i/(ωC)) - V₀/2]exp(iωt) 
  = [(V₀R' - V₀R'/2 + iV₀/(2ωC))/(R' - i/(ωC))]exp(iωt).
  V_out = (V₀/2)(R' + i/(ωC))/(R' - i/(ωC))exp(iωt) = (V₀/2)exp(i(ωt + 2φ)).
  tanφ = 1/(R'ωC

Problem:

A student measures voltage drops in an AC circuit using three voltmeters and arrives at the following measurements:

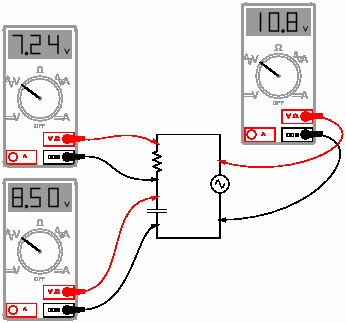
Upon viewing these measurements, the student becomes very perplexed.  Aren't voltage drops supposed to add in series, just as in DC circuits?  Why, then, is the total voltage in this circuit only 10.8 volts and not 15.74 volts?   Explain the reason for the "discrepancy" in the voltage measurements. Show that at any point in time Kirchhoff's loop rule is satisfied.

Solution:

• Concepts:
  AC circuits
• Reasoning:
  We have a series RC circuit.
• Details of the calculation:
  V = V₀ exp(iωt),  I = V/(Z_C + R). 
  V_R = IR = VR/(Z_C + R),  V_C = IZ_C = VZ_c/(Z_C + R), V_R + V_C = V.
  The AC voltages add in series, but phase must be considered. Multi-meters display no phase information, just RMS voltages.
  Z = R - i/(ωC) = (R² + 1/(ωC)^½)exp(iφ) = |Z|exp(iφ).  Here tanφ = -1/(ωRC)
  V_R = VRexp(-iφ) /|Z|,  V_C = V(-i/(ωC))exp(-iφ)/|Z|,
  V_R + V_c = V|Z|exp(iφ)exp(-iφ)/|Z| = V.