RL circuits (AC)

Problem:

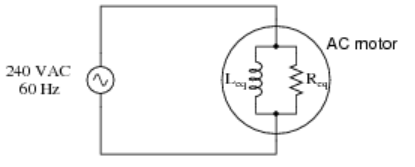
A large AC electric motor under load can be considered as a parallel combination of resistance and inductance.  If the equivalent resistance is 20 Ω and the inductance is 238 mH, calculate the rms current delivered by the 60 Hz, V_rms = 240 V AC power supply.

Solution:

• Concepts:
  AC circuits
• Reasoning:
  We are analyzing a parallel RL circuit.
• Details of the calculation:
  I_rms = V_rms/|Z|.
  Z = RZ_L/(R + Z_L) = (ω²L²R + iωLR²)/(R² + ω²L²)
  = ωLR(R² + ω²L²)^½/(R² + ω²L²)exp(iφ) = ωLR/(R² + ω²L²)^½exp(iφ) = |Z|exp(iφ).
  |Z| = 19.52 Ω.
  I_rms = V_rms/|Z| = (240 V)/(19.52 Ω) = 12.3 A.

Problem:

In an AC circuit, a filter circuit or filter removes unwanted frequency components from an input.  A passive filter consists of a circuit with at least one reactive component.  A filter with a single reactive component, either a capacitor or an inductor, is called a first-order filter.  Filters are described according to their behavior.  A low-pass filter will pass all signals below a specific frequency, but will attenuate or block signals of a higher frequency.  A high-pass filter will do just the opposite.  The boundary line is somewhat arbitrary since there exists a "transition zone".  The cutoff frequency is defined as the frequency at which |V_out| = 2^-½|V_in|.
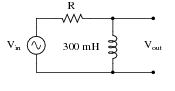
Inspect the filter shown below.  Identify what type of filter this circuit is, and calculate the size of resistor necessary to give it a cutoff frequency of 3 kHz:

Solution:

• Concepts:
  AC circuits
• Reasoning:
  We have a series RL circuit.
• Details of the calculation:
  Z = R + iωL.
  We want V_out = V_in Z_L/Z = V_inexp(iφ)ωL/(R² + (ωL)²)^½ = (1/√2)V_inexp(iφ).
  We need R  = ωL = 2π*3*10³*3*10^-1 Ω = 5.65 kΩ.
  This is a high-pass filter.

Problem:

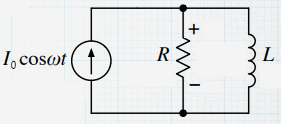
In this circuit with an AC current source, find the voltage across the resistor.
Let I₀ = 20/3 mA,  ω = 5*10⁴/s, R = 750 Ω, and L = 15 mH.

Solution:

• Concepts:
  AC circuits
• Reasoning:
  We have a parallel RL circuit.
• Details of the calculation:
  V = IZ.  I = I₀exp(iωt).
  The equivalent impedance is
  Z = Z_RZ_L/(Z_R + Z_L) = iRωL/(R + iωL).
  Z = R/(1 - iR/ωL) = R/(1 + R²/(ωL)²)^½exp(iφ) with tanφ = R/ωL.
  Z = 530.33 exp(iπ/4).
  V = 3.54 exp(iπ/4) V is the voltage across the resistor.