RLC circuits (AC)

Problem:

A series RLC circuit is driven by a generator with an emf amplitude of 80 V and a current amplitude of 1.25 A.  The current leads the emf by 0.65 rad.  What are the impedance and the resistance of the circuit?

Solution:

• Concepts:
  AC circuits
• Reasoning:
  We have a series RLC circuit and a AC generator, generating a sinusoidal voltage.
• Details of the calculation:
  In general: V = IZ
  Z = R + iωL + 1/(iωC) = R + i(ωL - 1/(ωC)) = (R² + (ωL - 1/(ωC))²)^½exp(iφ)
  φ = tan^-1((ωL - 1/(ωC))/R)
  All that is needed for this problem:
  Z = R + iX.
  Given:  V = 80 V exp(iωt), I = 1.25 A exp(i(ωt + 0.65)),
  Z = V/I = 64 Ω exp(-i0.65),  R =  64 Ω cos(0.65) = 50.95 Ω.

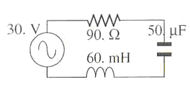
Problem:

In the circuit below a 30 V (peak) AC source at 60 Hz is connected to a 90 Ω resistor, a 50 μF capacitor, and a 60 mH inductor in series.  Find the phase of the current through the circuit with respect to the voltage across the source.

Solution:

• Concepts:
  AC circuits
• Reasoning:
  We are asked to analyze an AC circuit.
• Details of the calculation:
  V = IZ.
  Z = R + iωL + 1/(iωC) = [90 + i*22.6 - i*53)] Ω.
  = [90 - i*30.4] Ω = 95 exp(iφ) Ω with φ = -0.326.
  I = V/Z = (30 V)/(95 exp(-i0.326)) Ω = 0.316 A exp(i0.326).
  The peak value of the current is 0.316 A.
  φ_I - φ_V = 0.326.  I(t) leads V(t).

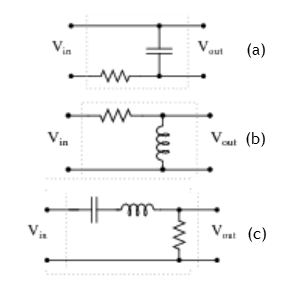
Problem:

For the circuits shown below, V_in = V₀exp(iωt).
In terms of R L and C find V_out and identify which type of filter each circuit represents.

Solution:

• Concepts:
  Filter circuits
• Reasoning:
  We are asked to analyze 3 different AC filter circuits.
• Details of the calculation:
  (a)  I = V_in/(Z_C + Z_R),  V_out = IZ_C = V_inZ_C/(Z_C + Z_R).
  Z_C/(Z_C + Z_R) = 1/(1 + iRωC) = (1 - iRωC)/(1 + ω²R²C²) = [1/(1 + ω²R²C²)^½]e^-iφ.
  tanφ = RωC.
  V_out = V₀[1/(1 + ω²R²C²)^½]e^i(ωt-φ).
  V_out --> 0 as ω --> ∞,  V_out --> V₀ as ω --> 0, we have a low-pass filter.
  
  (b)   I = V_in/(Z_L + Z_R),  V_out = IZ_L = V_inZ_L/(Z_L + Z_R).
  Z_L/(Z_L + Z_R) = ωLexp(iπ/2)/(R + iωL) = exp(iφ)ωL/(R² + (ωL)²)^½.
  V_out = V₀[ωL/(R² + (ωL)²)^½]e^i(ωt+φ).
  V_out --> 0 as ω --> 0,  V_out --> V₀ as ω --> ∞, we have a high-pass filter.
  
  (c)   I = V_in/(Z_c + Z_L + Z_R),  V_out = IZ_R = V_inZ_R/(Z_C + Z_L + Z_R).
  Z_R/(Z_C + Z_L + Z_R) = exp(iφ) R/(R² + (ωL - 1/(ωC))²)^½.
  V_out = V₀[R/(R² + (ωL - 1/(ωC))²)^½]e^i(ωt+φ).
  V_out = V₀ when ω = 1/(LC)^½.
  V_out --> 0 as ω --> 0 and as as ω --> ∞, we have a band-pass filter.

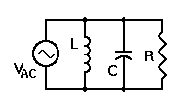
Problem:

Find the currents in each arm of the parallel LRC circuit with V_AC = Re(V₀e^iωt).   Find the total current and the average power drawn from the generator.

Solution:

• Concepts:
  AC circuits
• Reasoning:
  We have a parallel RLC circuit and a AC generator, generating a sinusoidal voltage.
• Details of the calculation:
  Let V = V₀e^iωt.  
  I_L = Re(V/Z_L) = Re(V/iωL) = Re((V₀/(ωL))e^{i(ωt - π/2)}) = (V₀/(ωL))cos(ωt - π/2)
  = (V₀/(ωL))sin(ωt).
  I_C = Re(V/Z_c) = Re(ViωC) = Re(V₀ωC e^{i(ωt + π/2}) = V₀ωC cos(ωt + π/2)
  = -V₀ωC sin(ωt).
  I_R = Re(V/R) = Re((V₀/R)e^iωt) = (V₀/R)cos(ωt).
  I_tot = V₀ [(1/(ωL) -  ωC)sin(ωt) + (1/R)cos(ωt)].
  P_avg = ½V₀²/R,  there is no energy dissipated in the reactive part.

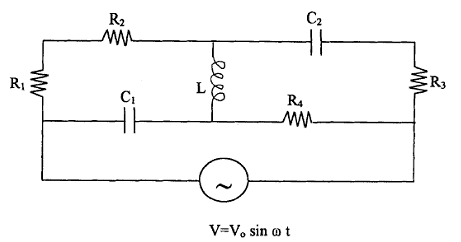
Problem:

For the circuit shown below, determine the value of the current output through the AC generator, in terms of the symbols given, for two limiting conditions.
(a)  The frequency of the AC generator approaches zero.
(b)  The frequency of the AC generator approaches infinity.

Solution:

• Concepts:
  AC circuits
• Reasoning:
  We have a two-terminal network and a AC generator, generating a sinusoidal voltage.
• Details of the calculation:
  Assume V(t) and I(t), are  proportional to exp(iωt).  Assume idealized circuit elements.  Define the impedance Z as Z = V/I.  Then
  Z(capacitance) = Z_C = 1/(iωC), 
  Z(inductance) = iωL,
  Z(resistance) = Z_R = R.
  (a)  As ω approaches zero the inductance becomes a short circuit and the capacitors become open circuit elements.  Then the circuit is just a simple loop with 3 resistors in series.  I = V₀ exp(iωt)/(R₁+R₂+R₄).
  (b)  As ω approaches infinity the capacitors become a short circuits and the inductor becomes an open circuit element.  The circuit then contains 2 loops in parallel, one with resistance R₄ and one with the resistors R₁ R₂ and R₃ in series.  The current through the AC generator is I = V₀ exp(iωt)(1/(R₁+R₂+R₃) + 1/R₄).

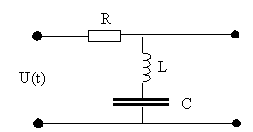
Problem:

On the input of the RLC filter shown below the periodic voltage oscillating as U(t) = A sin⁴(ωt) is applied.  Calculate the output voltage after all transients have decayed if the elements R, L, C have been chosen such that  4ω²LC = 1 and  ωRC = 2.

Solution:

• Concepts:
  AC circuits, Fourier series, the principle of superposition
• Reasoning:
  U = ZI for a sinusoidally varying voltage.
• Details of the calculation:
  sin⁴(x) = (1/8)cos(4x) - ½cos(2x) + 3/8.
  Use complex notation, the real part of the expression describes the physical quantity.
  U(t) = (A/8)exp(i4ωt) + (A/2)exp(i2ωt) + 3A/8 = U₁ + U₂ + U₃.
  Use the principle of superposition.
  For each of the 3 terms in the Fourier series:  U_i = IZ_i, U_i' = IZ_i', U_i' = U_iZ_i'/Z_i.
  Here U_i is the input and U_i' the output voltage.
  Z_i/Z_i' = (i(ω_iL - 1/(ω_iC)) + R)/(i(ω_iL - 1/(ω_iC))) = 1 - iω_iRC/(ω_i²LC - 1).
  Z_i/Z_i' = [1 + (ω_iRC/(ω_i²LC - 1))²]^½ exp(-iφ), with tanφ = ω_iRC/(ω_i²LC - 1).
  Z_i'/Z_i = [1 + (ω_iRC/(ω_i²LC - 1))²]^-½ exp(iφ).
  For ω_i = 0, Z_i'/Z_i = 1.
  For ω_i = 2ω, Z_i'/Z_i =  i(4ω²LC - 1)/(i(4ω²LC - 1) + 2ωRC) = 0.
  For ω_i = 4ω, Z_i'/Z_i = [1 + (4ωRC/(16ω²LC - 1))²]^-½ exp(iφ) = [1 + (8/3)²]^-½ exp(iφ) = 0.3511exp(iφ).
  U' = 3A/8 + (A/8)exp(i(4ωt + φ) = 3A/8 - 0.3511(A/8)cos(4ωt + φ).
  The filter passes only the 4ω component (plus a constant offset).

Problem:

Consider a series RLC circuit. The circuit is driven by a sinusoidal voltage V(t) = V₀exp(iωt).  The resonant frequency of the circuit is ω = ω₀ = 1/√(LC).
(a)  Solve for the current I(t) in the circuit.
(b)  Find the voltage V_L across the inductor.  For which frequency ω_max is |V_L| largest?
(b)  Find the average power dissipated by the circuit at the resonant frequency ω₀.

Solution:

• Concepts:
  AC circuits
• Reasoning:
  We are asked to analyze an AC circuit.
• Details of the calculation:
  (a)  V = IZ.
  Z = R + iωL + 1/(iωC) = R + i(ωL - 1/(ωC)) = (R² + (ωL - 1/(ωC))²)^½exp(iφ).
  φ = tan^-1((ω²LC - 1)/(ωRC)).
  I = V/Z = [V₀/(R² + (ωL - 1/(ωC))²)^½]exp(i(ωt - φ)).
  If ω = ω₀ = 1/√(LC) then I = [V₀/R]exp(iω₀t - φ).
  
  (b)  V_L = I Z_L = VZ_L/Z.
  Z_L/Z = iωL /(R + iωL + 1/(iωC))
  = iωL(R - i(ωL - 1/(ωC))/(R² + (ωL - 1/(ωC))²)
  = ωL(iR + (ωL - 1/(ωC))/(R² + (ωL - 1/(ωC))²)
  = ωLexp(iφ')/(R² + (ωL - 1/(ωC))²)^½.
  |Z_L/Z| = ωL/(R² + (ωL - 1/(ωC))²)^½.
  d|Z_L/Z|/dω = L/(R² + (ωL - 1/(ωC))²)^½ - ωL(ωL - 1/(ωC))(L + 1/(ω²C)))/(R² + (ωL - 1/(ωC))²)^3/2.
  = L[(2/C)((1/(ω²C) - L) + R²]/(R² + (ωL - 1/(ωC))²)^3/2.
  d|Z_L/Z|/dω = 0 --> (2/C)((1/(ω²C) - L) + R² = 0,
  1/ω_max² = LC - R²C²/2 = (1/ω₀²)(1 - ½R²C/(Lω₀²)).
  ω_max² = ω₀²/(1 - ½R²C/(Lω₀²)).
  If R << (L/C)^½ then ω_max ≈ ω₀.
  
  (c)  P = Re(I)Re(V) = |I||V|cos(ωt) cos(ωt - φ)
  = |I||V|(cos²(ωt) cos(φ) + cos(ωt) sin(ωt) sin(φ)).
  P_avg = ½|I||V|cos(φ) = ½Re(VI*).
  If ω = 1/√(LC) then I = [V_in/R]exp(iωt).
  P_avg = ½V_in²/R = V_{in_rms}²/R.