Ladder circuits (AC)

Problem:

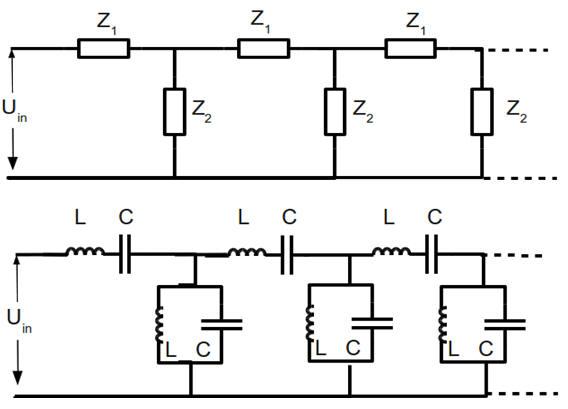
(a)  Calculate the impedance Z of an infinite chain of elements with impedances Z₁ and Z₂, as shown in the top figure.
(b)  Calculate Z₁ and Z₂ for the specific case shown in the bottom figure.

Solution:

• Concepts:
  Ac circuits, ladder networks

• Reasoning:
  We treat the circuit as an infinite ladder network with characteristic impedance Z.
  Since the ladder is infinite, the impedance Z will not change if an additional section is added to the front of ladder. 

• Details of the calculation:
  (a)  An equivalent network with impedance Z is shown in the figure.
  
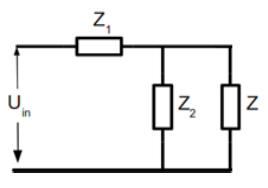
  Z = Z₁ + ZZ₂/(Z + Z₂),  Z² - Z₁Z - Z₁Z₂ = 0,  Z = Z₁/2 + (Z₁²/4 + Z₁ Z₂)^½.
  (b)  For the network in the bottom figure
  Z₁ = iωL - i/(ωC) = (i/(ωC))(ω²LC - 1),  Z₂ = (-iωL)/(ω²LC - 1).
  Z₁² = (-1/(ωC)²)(ω²LC - 1)²,  Z₁ Z₂ = L/C.

Problem:

Consider the "twin-T" band-pass filter as shown below.  Find the highest and lowest frequency passed by this filter if it is properly terminated.

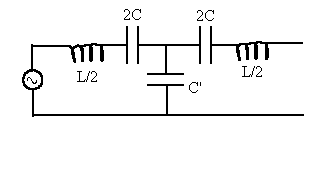
Solution:

• Concepts:
  Ac circuits, ladder networks

• Reasoning:
  In order to act as a filter, the circuit must be terminated with the characteristic impedance Z₀ of the ladder network.  Z₀ = (Z₁²/4 + Z₁Z₂)^½ if the sections of the ladder look as shown below.

  

  If Z₀² > 0 the frequency is passed.
  If Z₀² < 0 the frequency is not passed.  (The circuit absorbs no power.)

• Details of the calculation:
  We treat the circuit as an infinite ladder network with characteristic impedance Z₀.
  Z₀ = (Z₁²/4 + Z₁Z₂)^½.
  Z₁ = iωL + 1/(iωC),  Z₂ = 1/(iωC').
  Z₁² = -ω²L² - 1/(ω²C²) + 2L/C.
  Z₁Z₂ = L/C' - 1/(ω²C'C).
  Z₀² = L/2C + L/C' - ω²L²/4 - 1/(4ω²C²) - 1/(ω²C'C) 
  = (LC'+2LC)/(2CC')  - ω²L²/4 - (¼ + C/C')/(ω²C²).
  Set Z₀² = 0, then ω²(LC'+2LC)/(2CC')  - ω⁴L²/4 - (¼ + C/C')/C² = 0.
  Quadratic equation in ω²:  ω² = 1/(LC) +2/(LC') ± 2/(LC').
  ω_min² = 1/(LC),  ω_max² = 1/LC + 4/(LC')
  If ω ≈ 0, Z₀² <  0 the frequency is not passed.
  If ω --> ∞,Z₀² < 0 the frequency is not passed.
  Frequencies between ω_min² = 1/(LC) and ω_max² = 1/LC + 4/(LC') are not filtered out.