Transients, RC circuits

Problem:

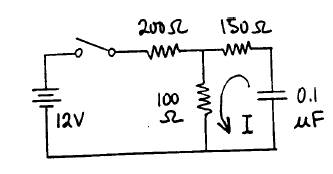
In the circuit shown, the switch is opened at t = 0, after having been closed for a long time.  Find the current I as a function of time for t > 0.

Solution:

• Concepts:
  RC circuits
• Reasoning:
  While the switch is closed the charge on the capacitor is Q = CV.
  When the switch is opened the capacitor discharges through the resistor.
• Details of the calculation:
  While the switch is closed the voltage across the capacitor is 4 V.
  When the switch is opened the capacitor discharges through a 250 Ω resistor.
  V = V₀exp(-t/τ),  τ = RC.
  V = (4 V)exp(-t/(2.5*10^-5 s)).
  I = V/R  = (1.6*10^-2 A) exp(-t/(2.5*10^-5 s)).

Problem:

Consider the RC circuit below with a switch S that can be opened and closed.

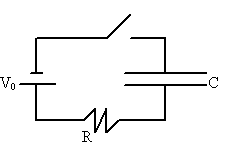
The capacitor is uncharged when, at t = 0, the switch is closed.  Current begins to flow and the capacitor will charge. 
(a)  Write the equation relating the charge on the capacitor Q(t) and the current in the circuit I(t) to V₀ and time. 
(b)  Solve for the voltages V_C(t) across the capacitor and V_R(t) across the resistor.
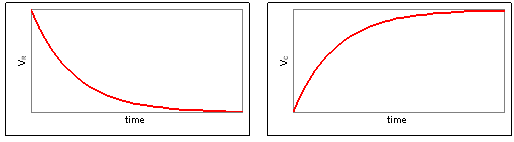
(c)  Sketch V_C(t) and V_R(t).

 Solution:

• Concepts:
  RC circuits
• Reasoning:
  We are asked to analyze the transient behavior of an RC circuit.
• Details of the calculation:
  (a)  V₀ - RdQ/dt - Q/C = 0,   dQ/dt = I(t) = V₀/R - Q/(RC). 
  (b)  Q(t) = CV₀(1 - exp(-t/(RC)),   V_C(t) = V₀(1 - exp(-t/(RC)), 
   I(t) = (V₀/R)exp(-t/(RC)),   V_R(t) = V₀exp(-t/(RC).
  (c) 
   
   

Problem:

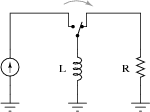
(a)  Suppose a capacitor is charged by a voltage source, and then switched to a resistor for discharging.  Would a larger capacitance value result in a slower discharge, or a faster discharge?  How about a larger resistance value? 

(b)  Now consider an inductor, "charged" by a current source and then switched to a resistor for discharging.  Would a larger inductance value result in a slower discharge, or a faster discharge?  How about a larger resistance value?

Solution:

• Concepts:
  Transients in circuits
• Reasoning:
  The transient behavior of a circuit is characterized by is time constant τ.
• Details of the calculation:
  (a)  τ = RC.
  Larger capacitance --> slower discharge
  Larger resistance --> slower discharge
  (a)  τ = L/R.
  Larger inductance --> slower discharge
  Larger resistance --> faster discharge

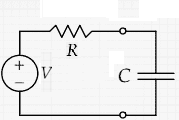
Problem:

(a)  In the RC circuit shown, V abruptly changes value from V₁ to V₂ at t = 0 after having been at V₁ for a long time.  Find the expression for the capacitor voltage as a function of time.

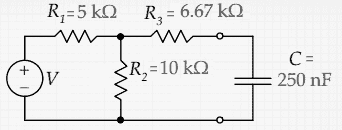
(b)  In the RC circuit shown, V abruptly changes value from V₁ = 6 V to V₂ = 15 V at t = 0 after having been at V₁ for a long time.  Find the expression for the capacitor voltage as a function of time.

Solution:

• Concepts:
  Transients in circuits
• Reasoning:
  We are asked to analyze the transient behavior of an RC circuit.
• Details of the calculation:
  (a)  For t < 0 we have V_C(t) = V₁.  Q(t) = CV₁.
  For t > 0 we have
  dQ/dt = I(t) = V₂/R - Q/(RC). 
  Q(t) = CV₂ - C(V₂ - V₁)exp(-t/RC).
  V_C(t) = V₂ - (V₂ - V₁)exp(-t/RC).
  
  (b)  There are different approaches to analyzing this circuit.
  (i)  Using Kirchhoff's rules:
  Use SI units, measure resistance in Ω, voltages in V and C in Farad.
  For t > 0 we have
  15 - 5*10³I₁ - 10⁴I = 0.
  Q/C - (20*10³/3)I₂ - 10⁴I = 0.
  I₁ + I₂ = I.  I₂ = -dQ/dt.
  
  Eliminate I₁ = I - I₂:
  15 - 15*10³I + 5*10³I₂ = 0.
  
  Eliminate I:
  I = 1*10^-3 + I₂/3.
  Q/C - (10⁴)I₂ - 10I = 0.
  dQ/dt = 10^-3 - Q/(10⁴C).
  
  Assume Q = A - Bexp(-t/x).
  dQ/dt = -Q/x + A/x
  x = 10⁴C = 2.5*10^-3s,  A = 10C.
  Q(t) = 10C - Bexp(-t/2.5*10^-3 s).
  V_C(t) = 10 V - (B/C)exp(-t/2.5*10^-3 s).
  Initial condition:  V(0) = (2/3)6 V = 4 V.
  B/C = 6 V.
  V_C(t) = 10 V - 6 V exp(-t/2.5*10^-3 s).
  
  (ii)  Using Thevenin equivalent circuits:
  
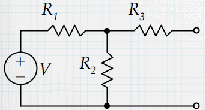
  ε_eff = VR₂/(R₁ + R₂) = 2V/3.
  Z_eff = R₃ + R₁R₂/(R₁ + R₂) = 10 kΩ.
  The equivalent circuit looks like this,
  
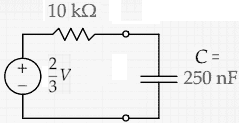
  V_C(t) = 10 V - 6 V exp(-t/(RC)) =   10 V - 6 V exp(-t/2.5*10^-3 s) .