Transients, RLC circuits

Problem:

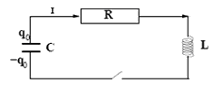
The capacitor shown in the circuit below initially holds a charge q₀.  The switch is closed at t = 0.  Find the charge on the capacitor as a function of time, if R²/4 < L/C.  What is the oscillation frequency of the circuit when R --> 0?

Solution:

• Concepts:
  RLC circuits
• Reasoning:
  We are asked to analyze the transient behavior of an RLC circuit.
• Details of the calculation:
  Q/C - IR - LdI/dt = 0.  I = - dQ/dt.  d²Q/dt² + (R/L)dQ/dt + Q/(LC) = 0.
  Let Q(t) = Aexp(-bt).  Then b² - b (R/L) + 1/(LC) = 0.
  b = R/(2L) ± (R²/(4L²) - 1/(LC))^½.
  If  R²/4 < L/C, then b = R/(2L) ± i(1/(LC)) - R²/(4L²))^½ = α ± iω.
  α = R/(2L), ω = (1/(LC)) - R²/(4L²))^½.  Q(t) = q₀exp(-αt)cos(ωt).
  When R --> 0 then α --> 0 and ω --> 1/(LC)^½.

Problem:

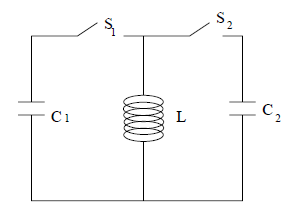
Consider the circuit below, where C₁ is initially charged to 75 V.  Assume that C₁ = 0.01 F, C₂ = 0.003 F, and L = 15 H.  Explain how to open and close the switches so as to discharge C₁ and charge C₂.  Starting at t = 0 give explicit times for opening and closing each switch.  What is the final voltage across C₂?

Solution:

• Concepts:
  RL transient circuits
• Reasoning:
  We are asked to analyze the transient behavior of an RL circuit.
• Details of the calculation:
  Assume that at t = 0 the switch S₁ is closed and the switch S₂ stays open.
  The equation of the circuit is Q/C₁ = -LdI/dt,  Ld²Q/dt² = -Q/C₁.
  Q = Q₁exp(iω₁t), where ω₁ = 1/(LC₁)^½. 
  After time t₁ = π/(2ω₁) the capacitor C₁ will be discharged, all the energy will be stored in the inductor.
  ½Q₁²/C₁ = ½LI_max².
  Q₁ = (0.01*75) = 0.75 C,  t₁ = 0.6 s, ½Q₁²/C₁ = 28.13 J,  I_max = 1.94 A.
  At t₁ we close S₂ and open S₁.  The equation of the circuit now is Q'/C₂ = -LdI/dt,  Ld²Q'/dt² = -Q'/C₂.
  I' = I_maxexp(iω₂(t-t₁)), where ω₂ = 1/(LC₂)^½.
  At time t₂ = π/(2ω₂) + t₁ the capacitor C₂ will hold the maximum charge Q₂ and no energy will be stored in the inductor.
  At time t₂ we open switch S₂.
  ½Q₂²/C₂ = ½LI_max².  V₂(final) = Q₂/C₂.
  t₂ = 0.94 s, Q₂ = 0.41 C.  V₂(final) = 137 V.

Problem:

A mass m fixed to a spring of spring constant k and immersed in a fluid provides a model for a damped harmonic oscillator.  A circuit with inductance L, capacitance C and resistance R provides an electric analog to such an oscillator.
(a) Write out the circuit equation for the LCR circuit and Newton's second law of motion for the damped oscillator.  What assumption must be made about the dependence of the damping of the mass on velocity for the two equations to have the same mathematical form?
(b)  How are the constants m, k, and b (damping constant) related to the circuit constants L, C and R?  To what parameters of the electric circuit are the mechanical quantities x (displacement) and v (velocity) related?
(c)  Derive and expression for the displacement and velocity in the limit of weak damping.
(d)  What voltages measured in the circuit would give values proportional to the displacement and velocity of the mechanical oscillator?

Solution:

• Concepts:
  RLC circuit, damped harmonic oscillator
• Reasoning:
  We are asked to compare the differential equation describing the behavior of a series LRC circuit with the equation of motion for a damped harmonic oscillator.
• Details of the calculation:
  (a)  LRC circuit:  Q/C = -IR - LdI/dt.  Ld²Q/dt² = -RdQ/dt - Q/C
  Damped oscillator:  md²x/dt² = -bdx/dt - kx.  We must assume that the magnitude of the damping force is proportional to the speed.

  (b)  d²Q/dt² = -(R/L)dQ/dt - Q/(LC),  d²x/dt² = -(b/m)dx/dt - (k/m)x.
  R/L --> b/m,  1/(LC) --> k/m.
  Possible substitutions:  L --> m,  R --> b, k --> 1/C.
  Q --> x,  I = dQ/dt --> v = dx/dt.

  (c)  Try x = x₀exp(at+ d).
  a² + ba/m + k/m = 0.  a = -b/2m ± ( b²/4m² - k/m)^½.
  x = x₀exp(-βt) cos(ωt + d),  β = b/2m,  ω² = k/m - β² = ω₀² - β².
  If the damping is weak then x ≈ x₀exp(-βt) cos(ω₀t + d).

  (d)  The voltage across the capacitor is proportional to Q --> x,  The voltage across the resistor is proportional to I --> v.