Energy and momentum flux (examples)

Problem:

(a)  Compare the intensity of a light bulb at a distance of 6 m from it to the intensity at 2 m from it.  Repeat this comparison for laser light.  Explain fully but briefly.
(b)  Compute the electric field corresponding to a focused light intensity of I = 10¹²W/cm², and compare the result with the electric field experienced by the electron in a hydrogen atom.

Solution:

• Concepts:
  The inverse square law, the Poynting vector, the electric field of a point charge
• Reasoning:
  (a)  The energy emitted by the bulb is emitted into a solid angle of 4π.  It is spread over an area that increases as 4πr² with distance r.
  (b)  The magnitude of the Poynting vector S = (1/μ₀)E×B relates the intensity of an electromagnetic wave to the field strength.  For a sinusoidal electromagnetic wave we have <S> = (|E₀²|/2)(ε₀/μ₀)^½.
  The electron in hydrogen atom experiences the electric field of a point charge q = 1.6*10^-19 C a distance a₀ = 5.29*10^-11 m from the point charge, E_q = q/(4πε₀a₀²) .
• Details of the calculation:
  (a)  For a light bulb we have:  Intensity = energy/(area * time) proportional to 1/r².
  Intensity at 6 m = (1/9) * intensity at 2 m.
  A laser beam with a Gaussian profile has a waist d₀.  It either diverges from or converges to this beam waist.  This divergence or convergence is measured by the angle θ  which is subtended by the points on either side of the beam axis where the irradiance has dropped if to 1/e² of its value on the beam axis.
  
  For a Gaussian beam of a particular wavelength, the product d₀θ is constant.  A highly collimated beam with small θ has a large beam waist d₀.  Over short distances, the change in d is negligible to d₀.  The intensity is therefore practically the same at 2 m and at 6 m.

  (b)  10¹²W/(0.01 m)² = (|E₀²|/2)(ε₀/μ₀)^½,  E₀ = 2.74*10⁹ N/C is the electric field of the light wave.
  E_q = q/(4πε₀a₀²) = 5.15*10¹¹ N/C is the electric field experienced by the electron in a Hydrogen atom.
  E_q >> E₀.

Problem:

A plane electromagnetic wave of intensity 6 W/m² strikes a small pocket mirror of area 40 cm² held perpendicular to the approaching wave.
(a)  What momentum does the wave transfer to the mirror each second?
(b)  Find the magnitude of the force that the wave exerts on the mirror.

Solution:

• Concepts:
  Energy and momentum flux of an electromagnetic wave, radiation pressure
• Reasoning:
  The energy flux of an electromagnetic wave is given by the Poynting vector S.  Its magnitude is the intensity.  The momentum flux is S/c.  The wave is reflected by the mirror.  The momentum transferred to the mirror per unit area per second is twice the momentum of the light striking the mirror per unit area per second.
• Details of the calculation:
  (a)  dp/dt = 2(1/c)S∙A.
  S∙A = (6 W/m²)(4*10^-3 m²) = 0.024 W.
  dp/dt = 2*0.024 W/(3*10⁸ m/s) = 1.6*10^-10 kgm/s².
  Each second the wave transfers 1.6*10^-10 kgm/s of momentum to the mirror in the incident wave direction.
  (b)  F = dp/dt = 1.6*10^-10N.

Problem:

A beam of light with an intensity of 10⁸ W/m² traveling in free space hits normally on a lossy mirror.  The mirror reflects 60% of the light and absorbs 40%.  What is the resulting radiation pressure on the surface of the mirror?

Solution:

• Concepts:
  Momentum transported by an EM wave
• Reasoning:
  The momentum of an object absorbing the radiation changes.  The rate of change is dp_perp/dt = (1/c)SA_perp, where A_perp is the cross-sectional area of the object perpendicular to the direction of propagation of the electromagnetic wave. (We assume a massive object absorbing a negligible fraction of the energy.)
  If the radiation is reflected instead of absorbed, then its momentum changes direction. The radiation pressure on an object that reflects the radiation is therefore twice the radiation pressure on an object that absorbs the radiation.
• Details of the calculation:
  Momentum flux of incident wave: S/c = (10⁸ W/m²)/c
  Force exerted on an area A of the mirror:  0.4*(S/c)A + 0.6*(2S/c)A
  Radiation pressure:  P = 0.4*(1/3) N/m² + 0.6*(2/3) N/m² = 8/15 N/m²

Problem:

It has been proposed to drive a spacecraft remotely by directing an intense electromagnetic beam to the craft.
(a)  Is it more efficient to absorb the beam or reflect it from the craft?
(b)  If the beam carries 10⁶ watts uniformly in an area of 5 m² and the beam is reflected, how long would it take for a 1000 kg spaceship to reach a final velocity of 10⁶ m/s, and how far would the craft travel in this time?

Solution:

• Concepts:
  Energy and momentum flux for an electromagnetic wave, momentum conservation
• Reasoning:
  Electromagnetic waves carry energy and momentum. When an EM wave is absorbed or reflected, momentum must be conserved.
• Details of the calculation:
  (a)  Approximately twice as much momentum is transferred by reflecting the beam than by absorbing the beam.  Nonrelativistic kinematics can be used.
  (b)  <S> = 2*10⁵ W/m² = energy flux.
  <S>/c = momentum flux.
  dp/dt = 2*<S>A/c = 2*10⁶ W/c = (2/3)*10^-2 N.
  dv/dt = (2/3)*10^-5 m/s².
  t = 10⁶ s/((2/3)*10^-5) = 1.5*10¹¹ s.
  d = ½*(2/3)*10^-5(1.5*10¹¹)² m = 7.5*10¹⁶ m = 7.9 ly.

Problem:

By considering the Poynting vector S = (1/μ₀)(E×B) comment as quantitatively as possible on the energy flow in the following situations:
(a)  a long cylindrical wire of conductivity σ carrying a current I.
(b)  a stationary electric charge q sitting on top of a magnetic dipole with magnetic moment m.

Solution:

• Concepts:
  The Poynting vector, energy conservation
• Reasoning:
  The Poynting vector represents the energy flux in the electromagnetic field.  The energy can circulate or flow into an object.  If it flows into an object and is absorbed, energy conservation requires that the field energy is converted into another form of energy.
• Details of the calculation:
  (a)  In the wire j = σE.  Let j = j k, I = jπR² = σEπR².  E = I/(σπR²).
  On the surface of the wire E = I/(σπR²) k.
  Outside of the wire B = (φ/φ) μ₀I/(2πr).  On the surface B = (φ/φ) μ₀I/(2πR). 
  S = (1/μ₀)(E×B).  S = -(ρ/ρ) I²/(2σπ²R³).
  Energy is flowing into the wire and is converted into heat.
  [The field energy that is flowing into the wire per unit length is P = S2πR = I²/(σπR²).
  The thermal energy dissipated per unit length is P = I²R_{res per unit length}.
  R_{res per unit length} = 1/(σπR²), since j = σE,  πR²j = πR²σE, or,
  I = πR²σV/l = V/R_res,  R_res = l/(πR²σ).
  Therefore thermal energy dissipated per unit length = field energy flowing into the wire per unit length.]
  
  (b)  Assume the point charge and the magnetic dipole are located at the origin with m = m k.
  E = [1/(4πε₀)] (q/r²) (r/r),  B = [μ₀/(4π)] (m/r³)(2cosθ (r/r) + sinθ (θ/θ)).
  S = (1/μ₀)(E×B), S = 1/(16π²ε₀) (mq/r⁵) sinθ (φ/φ).
  Field energy circulates about the z-axis in the (φ/φ) direction.

Problem:

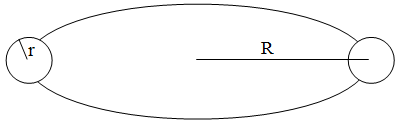
An "air core" toroid of mean radius R and cross-sectional area πr² is wound with N turns of wire.  (r << R).  A current with a time dependence I(t) = Kt is turned on at t = 0.
(a)  Find the energy stored in the magnetic field at time t.
(b)  Find the direction and magnitude of the Poynting vector at a point just inside the toroid at time t.
(c)  Using the Poynting vector, find the rate of change of the field energy inside the toroid at time t.  Check your answer with that of part (a).

Solution:

• Concepts:
  The Poynting vector
• Reasoning:
  The Poynting vector represents the energy flux in the electromagnetic field.
• Details of the calculation:
  
  (a)  B inside the torus is tangential the to a circle with radius R (right-hand rule) with approximately constant magnitude
  B(t) = μ₀nI(t) = μ₀NI(t)/(2πR) = μ₀NKt/(2πR)
  The energy stored in the magnetic field inside the torus is
  U_mag = (1/(2μ₀))B²*πr²*2πR = μ₀N²K²t²r²/(4R)
  (b)   The flux of B through a loop encircling the inner surface of the torus is B(R)πr².  If this flux changes an electric field is induced.
  The  electric field just inside the torus is tangential to a circle with radius r (Lenz's rule) with magnitude given by 
  2πr*E = πr²∂B/∂t =  μ₀Nkπr²/(2πR).  E = μ₀Nkr/(4πR)
  S = (1/μ₀)(E×B), S = μ₀N²k²tr/(8π²R²) pointing everywhere towards the center circle (r = 0) of the torus.
  (c)  P = ∫_A(S∙n)dA  = S*2πR*2πr = μ₀N²K²tr²/(2R) = dU_mag/dt.

Problem:

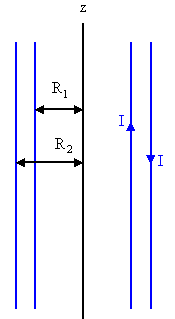
A long coaxial cable consists of two concentric cylindrical conducting sheets of radii R₁ and R₂ respectively (R₂ > R₁).  The two conductors are connected to a battery which maintains a voltage V₀ between them.  They carry equal and opposite currents I.
(a)  Use Ampere's law to calculate the magnetic field everywhere.
Plot the magnetic field as a function of r (use cylindrical coordinates).
(b)  Use Gauss' law to show that the electric field between the two conductors is
E(r) = Cr/r².  Express C in terms of R₁, R₂, and V₀.  (Here r is a cylindrical coordinate.)
(c)  Calculate the Poynting vector.  Show that the power carried by the cable is P = V₀I.

Solution:

• Concepts:
  Gauss' law, Ampere's law, the Poynting vector S = (1/μ₀)(E×B)
• Reasoning:
  We are instructed to use Gauss' law and Ampere's law and to calculate the Poynting vector.
• Details of the calculation:
  
   
  • (a)  For a circular loop Γ of radius r, concentric with the z-axis and lying in the x-y plane  we have
    2πrB = μ₀I_{through Γ}.  B = B (φ/φ).
    r > R₂:  B = 0.
    r < R₁:  B = 0.
    R₁ < r < R₂:  B = (φ/φ) μ₀I/(2πr).
    (b)  For a Gaussian surface in the form of a cylinder with radius r and length L and its axis on the z-axis we have
    2πrE_rL = λ_insideL/ε₀.  E_r = λ_inside/(2πε₀r)(r/r)
    For a current to flow in the conductor in a static situation we need a voltage.
    ∫_R1^R2 E∙dr = V₀.  ∫_R1^R2 E∙dr = λ/(2πε₀)[lnR₂ - lnR₁),  λ = 2πε₀V₀/ln(R₂/R₁).
    E_r = V₀/(ln(R₂/R₁))(r/r²).
    If the conductors have no resistance, the electric field only has a radial component.
    (c)  Assume E = V₀/(ln(R₂/R₁))(r/r²), i.e. the conductors have no resistance.
    Then S = (1/μ₀)(E×B), S = k IV₀/[2πr² ln(R₂/R₁)].
    P = ∫S∙n dA = ∫_R1^R2 2πrdr IV₀/[2πr² ln(R₂/R₁)] = [IV₀/ln(R₂/R₁)]∫_R1^R2 (1/r)dr = IV₀.
    P is the power flowing between the conductors into the k direction.

Problem:

Consider two concentric spherical metal shells of radius a and b, a < b.  There is a charge +q on the inner and a charge -q on the outer sphere.  A magnetic dipole with dipole moment m is in the center of the inner sphere.  Find the angular momentum associated with the electromagnetic field of the system.

Solution:

• Concepts:
  The Poynting vector, energy momentum and angular momentum density in the electromagnetic field.
• Reasoning:
  S = (1/μ₀)(E×B) is the energy flux.  The momentum flux is S/c.  (Photon energy: hf, photon momentum: hf/c.)
  The momentum flux equals the moment density times c.
  When S is circulating the angular momentum density will not be zero.
• Details of the calculation:
  Assume the magnetic dipole is located at the origin with m = m k.
  Then B = [μ₀/(4π)](m/r³)(2cosθ (r/r) + sinθ (θ/θ)).
  The electric field is nonzero only between the shells.
  E = [1/(4πε₀)](q/r²) (r/r) between the shells.
  S = (1/μ₀)(E×B), S = [1/(16π²ε₀)](mq/r⁵) sinθ(φ/φ).
  Field energy circulates about the z-axis in the (φ/φ) direction.
  The  momentum density in the field is g = S/c²,
  and the angular momentum density is r×g.
  sinθ (φ/φ)= (r×z)/(rz)
  r×(r×z) = (r∙z)r - (r∙r)z = rz cosθ r - r² z.
  L = ∫_V r×g dV = -[mq/(16π²ε₀c²)]∫_V dV (cosθ(xi + yj + zk)/r⁵ - (1/r⁴)k)
  = [mq/(16π²ε₀c²)]k[∫_a^b 4πr²dr/r⁴ - ∫_a^b ∫₀^π 2πr²dr sinθdθ  rcos²θ/r⁵]
  The x and y components of L vanish from symmetry.
  L = [mq/(4πε₀c²)]k[(1/a - 1/b) - (1/a - 1/b)∫₀^π cos²θ sinθdθ]
  = ⅔mq/(4πε₀c²)][(1/a - 1/b)k.

Problem:

A (locally) plane electromagnetic wave in vacuum is propagating in the positive z-direction.  The angular frequency of the wave is ω.  The wave generator slowly decreases the amplitude of the wave.  At the position z = 0 the amplitude of the wave is E₀(1 - at) for times between t = 0 and t = 1/a, with a << ω.
Consider a cylindrical surface as shown.

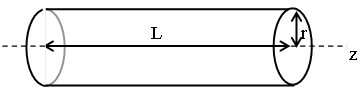
(a)  Find the average outward energy flux from the cylinder.
(b)  Find the field energy enclosed by the surface, and show that it decreases at a rate equal to the flux found in part (a).

Solution:

• Concepts:
  The Poynting vector, energy density
• Reasoning:
  The Poynting vector represents the energy flux.
• Details of the calculation:
  (a)  At z = 0 and t = t₀ we have E(0,t₀) = E₀(1 - at₀) cos(ωt₀).
  The field at z = L and t = t₀ is the same as the field at z = 0 and t = t₀ - L/c.
  E(L,t₀) = E₀(1 - a(t₀ - L/c) cos(ω(t₀ - L/c)).
  S = (1/μ₀)(E×B) = k (1/μ₀)E² = k ε₀c E².
  S points in the z-direction, so the integral of S∙n over the surface of the cylinder reduces to an integral over the ends of the cylinder.
  ∮ S∙n dA = ε₀cπr²E₀²[(1 - at₀ + aL/c²)cos²(ωt₀ - L/c) - (1 - at₀)²cos²(ωt₀)].
  Since a <<  ω, averaging over one period of the oscillation yields
  ∮ <S>∙n dA = ½ε₀cπr²E₀²[(1 - at₀ + aL/c²) - (1 - at₀)²]
  = ½ε₀cπr²E₀²[(1 - at₀)(2aL/c) + (aL/c)²].

  (b)  The energy density is u = (1/(2μ₀))B² + (ε₀/2)E² = ε₀E².
  The energy density averaged over one period is <u> =  (ε₀/2)E².
  The average energy inside the cylinder at t = t₀  therefore is
  U = (ε₀/2)πr²E₀²∫₀^Ldx (1 - at + ax/c)² = ½ε₀cπr²E₀²(ax/c - at + 1)³/(3a)|₀^L.
  U = ½ε₀cπr²E₀²[(aL/c - at + 1)³/(3a) - (1 - at)³/(3a)].
  U decreases at a rate
  dU/dt = ½ε₀cπr²E₀²[-(aL/c - at + 1)² + (1 - at)²]
  = -ε₀cπr²E₀²[(1 - at)(2aL/c) + (aL/c)²].
  At t = t₀, the rate at which W decreases equals the average outward energy flux from the cylinder.