Maxwell's equations, (charge conservation, wave equation)

Problem:

(a)  By applying charge conservation to a volume V, derive the integral form of the equation of charge conservation.  Deduce the equation of continuity, ∇∙j + (∂/∂t)ρ = 0.
(b)  Show that the equation of continuity is a consequence of Maxwell's equations.
(c)  A region containing a charge Q₀ is produced at time t = 0 inside a conductor of conductivity σ.  By considering the flow of current across the surface of the region, show that at subsequent times the charge inside the region is Q(t) = Q₀exp(-σt/ε₀).
HINT:  Use Gauss' Law and Ohm's Law in the form j = σE.
(d)  Explain why you expect Q --> 0 as t --> ∞ .

Solution:

• Concepts:
  Gauss' theorem, Maxwell's equations, properties of a conductor
• Reasoning:
  (a)  If we have a conserved quantity in a volume V, then the rate at which it flows out of the volume must equal the rate it decreases inside the volume. 
  For charge this is expressed as ∫_{closed_A}j∙ndA = -(∂/∂t)∫_VρdV for any volume V.
  Gauss' theorem then yields ∫_V∇∙jdV = -(∂/∂t)∫_VρdV for any volume V.
  Therefore ∇∙j = -∂ρ/∂t.
  (b)  Maxwell's equations relate the sources and the fields.
• Details of the calculation:
  ∇×B = μ₀j + (1/c²)∂E/∂t (SI units), ∇∙(∇×B) = 0 --> μ₀∇∙j + (1/c²)(∂/∂t)∇∙E = 0.
  ∇∙E = ρ/ε₀, μ₀∇∙j + (1/(ε₀c²))(∂ρ/∂ t) = 0.
  μ₀ε₀ = 1/c², ∇∙j + (∂ρ/∂t) = 0.
  (c)  ∫_V∇∙jdV = -(∂/∂t)∫_VρdV.
  For a conductor we have j = σE.
  ∫_Vσ∇∙EdV = ∫_V(σρ/ε₀)dV = (σ/ε₀)Q = -(∂Q/∂ t).
  Q = Q₀exp(-σt/ε₀).
  (d)  In a conductor charges are free to move.  They will move and distribute themselves over the surface until the electric field inside the conductor is zero. 
  Q_inside ≠ 0 implies E_inside ≠  0, therefore we expect Q(t) = 0 as as t --> ∞ .

Problem:

(a)  Show that Maxwell's equations are consistent with the conservation of electric charge.
(b)  Show that the power P injected into a circuit by an electric field is given by ∫j∙E dV.  Verify that in steady state this reproduces the Ohmic heat loss in a "thin wire" approximation.

Solution:

• Concepts:
  Maxwell's equations
• Reasoning:
  (a)  If we have a conserved quantity in a volume V, then the rate at which it flows out of the volume must equal the rate it decreases inside the volume. 
  For charge this is expressed as ∫_{closed_A}j∙ndA = -(∂/∂t)∫_VρdV for any volume V.
  Gauss' theorem then yields ∫_V∇∙jdV = -(∂/∂t)∫_VρdV for any volume V.
  Therefore ∇∙j = -∂ρ/∂t.
• Details of the calculation:
  Maxwell's equations relate the sources and the fields.
  ∇×B = μ₀j + (1/c²)∂E/∂t (SI units), ∇∙(∇×B) = 0 --> μ₀∇∙j + (1/c²)(∂/∂t)∇∙E = 0.
  ∇∙E = ρ/ε₀, μ₀∇∙j + (1/(ε₀c²))(∂ρ/∂ t) = 0.
  μ₀ε₀ = 1/c², ∇∙j + (∂ρ/∂ t) = 0.
  Maxwell's equations are consistent with the conservation of electric charge.
  (b)  For a single charge, the rate of doing work by external fields B and E is qv∙E, in which v is the velocity of the charge.  Let ρdV = dq be the amount of charge in a volume element dV.
  dW/dt = dq v∙E = ρv∙E dV = j∙E dV = rate at which work is done by the field on the charges in dV.  The power P injected into a circuit is obtained by integration dW/dt over the volume of the circuit, P = ∫j∙E dV.  If we consider a steady current to a thin wire, then for an element of length dl and cross section dA of the wire, dV = dl∙dA.  In this approximation j is parallel to dl and E does not vary appreciably over the cross section of the wire.  Hence   ∫j∙E dV =  ∫j∙dA ∫E∙dl = IV = I²R  which is the Ohmic heat loss.

Problem:

Do the fields E = i E₀cos(ωt − kx ), B = 0  satisfy Maxwell's equations?
If a special condition for ρ and  j is needed, what is it?

Solution:

• Concepts:
  Maxwell's equations
  ∇∙E = ρ/ε₀,  ∇×E = -∂B/∂t,  ∇∙B = 0,  ∇×B = μ₀j + (1/c²)∂E/∂t
• Reasoning
  We are supposed to check if E = i E₀ cos (ωt − kx) is consistent with Maxwell's equations.
• Details of the calculation:
  ∇·E = ∂[E₀cos (ωt − kx)]/∂x = kE₀sin(ωt − kx) ≠ 0, ρ ≠ 0 .
  ρ = kε₀E₀sin(ωt − kx).
  Since B = 0, ∇·B = 0.
  ∇×E = 0,  ∂B/∂t = 0,  B = 0 is a possible solution.
  The equation of continuity follows from Maxwell's equations.
  ∇∙j = -(∂ρ/∂t) = -ωkε₀E₀cos(ωt − kx).
  Since B = 0, ∇×B = 0.  This requires j = (-1/μ₀c²)∂E/∂t = (ω/μ₀c²)E₀sin(ωt − kx)i.
  ∇∙j = ∂[(ω/μ₀c²)E₀sin(ωt − kx))]/∂x = (-kω/μ₀c²)E₀cos(ωt − kx) = -ωkε₀E₀cos(ωt − kx).
  The fields E = i E₀cos(ωt − kx ), B = 0  satisfy Maxwell's equations
  with ρ = kε₀E₀sin(ωt − kx) and j  = (ω/μ₀c²)E₀sin(ωt − kx)i.

Problem:

(a)  Write down Maxwell's equations in vacuum for a charge density and current density free medium (ρ = 0 and j = 0).
(b)  Show that the electric field and the magnetic field satisfy a wave equation.
(c)  Write down plane-wave solutions of the wave equations for the electric field and magnetic field.  How are they related to each other?  Find the group velocity and phase velocity of the electromagnetic waves.

Solution:

• Concepts:
  Maxwell's equations
• Reasoning:
  Maxwell's equations in free space yield the wave equation for both E and B.
• Details of the calculation:
  (a) ∇∙E = 0, ∇×E = -∂B/∂t, ∇∙B = 0, ∇×B = (1/c²)∂E/∂t.
  (b) ∇×(∇×E) = ∇(∇·E) - ∇²E = -(∂/∂t)(∇×B) = -μ₀ε₀∂²E/∂t².
  ∇²E = μ₀ε₀∂²E/∂t².
  ∇×(∇×B) = ∇(∇·B) - ∇²B = μ₀ε₀(∂/∂t)(∇×E) = -μ₀ε₀∂²B/∂t².
  ∇²B = μ₀ε₀∂²B/∂t².
  (c)  Plane wave solutions E = E((k/k)∙r - vt),  B = B((k/k)∙r - vt) exist. 
  (v = (μ₀ε₀)^-½ = c)  All plane wave solutions are linear superpositions of harmonic waves of the form sin(k∙r - ωt) and cos(k∙r - ωt), with ω/k = c.
  The phase velocity is ω/k = c, the group velocity is dω/dk = c.  There is no dispersion for EM waves in free space.

Problem:

Consider an electromagnetic traveling wave with electric and magnetic fields given by
E_x = E₀cos(kz - ωt) + φ),
and
B_y = B₀cos(kz - ωt) + φ).
Using Maxwell's equations show that B₀ can be written in terms of E₀.

Solution:

• Concepts:
  Maxwell's equations
• Reasoning:
  Maxwell's equations in free space  yield the wave equation for both E and B.   They can also be used to show that E ⊥ B,  E ⊥ k,  B ⊥ k,  B = (μ₀ε₀)^½(k/k)×E.
• Details of the calculation:
  From Maxwell's equations:
  ∇×E = -∂B/∂t.
  ∇×E = ∂E_x/∂z j = -kE₀sin(kz - ωt + φ) j,  -∂B/∂t = -ωB₀sin(kz - ωt + φ) j.
  Therefore kE = ωB₀,  B₀ = (k/ω)E₀.
  In free space k/ω = 1/c.

Problem:

Use Maxwell's equations to find the magnetic field of an EM wave in vacuum for which the electric field is given by 
E = (E_0xi + E_0yj)sin(ωt - kz + φ).

Solution:

• Concepts:
  Maxwell's equations
• Reasoning:
  Maxwell's equation in vacuum are
  ∇∙E = 0,  ∇×E = -∂B/∂t,  ∇∙B = 0, ∇×B = (1/c²)∂E/∂t.
  Using these equations we can derive the homogeneous wave equation for E and B and show that 
  E ⊥ B,  E ⊥ k,  B ⊥ k,  B = (1/c²)∂(k/k)×E.
• Details of the calculation:
  For the given plane wave:
  (∇×E)_x = ∂E_z/∂y - ∂E_y/∂z = k E_0ycos(ωt - kz + φ) = -∂B_x/∂t
  Therefore B_x = (k/ω)E_0ysin(ωt - kz + φ) = -(E_0y/c)sin(ωt - kz + φ)
  (∇×E)_y = ∂E_x/∂z - ∂E_z/∂x = -k E_0xcos(ωt - kz + φ) = -∂B_y/∂t
  Therefore B_y = (k/ω)E_0xsin(ωt - kz + φ) = (E_0x/c)sin(ωt - kz + φ)
  (∇×E)_z = ∂E_y/∂x - ∂E_x/∂y = -∂B_z/∂t = 0, therefore B_z = 0.
  (We are not interested in constant fields.)
  B = (1/c)(E_0xj - E_0yi)sin(ωt - kz + φ).

Problem:

Starting with Maxwell's equations:
(a)  Derive the wave equations for a light wave in vacuum.  Write out solutions for these equations for E and B.
(b)  Show that the electric and magnetic fields are in phase, perpendicular to each other and perpendicular to the direction of motion.
(c)  Determine the relative magnitude of the E and B fields.

Solution:

• Concepts:
  Maxwell's equations
• Reasoning:
  In regions where ρ and j are zero Maxwell's equations lead to the homogeneous wave equation for E and B.  All solutions can be viewed as linear superpositions of sinusoidal plane wave solutions.  Inserting these solutions into Maxwell's equations we derive (b) and (c).
• Details of the calculation:
  (a)  Maxwells equations in SI units are
  ∇∙E = ρ/ε₀,  ∇×E = -∂B/∂t,  ∇∙B = 0,  ∇×B = μ₀j + (1/c²)∂E/∂t
  Assume ρ and j are zero in the medium.
  ∇×(∇×E) = ∇(∇∙E) - ∇²E = -(∂/∂ t)(∇×B) = -μ₀ε₀∂²E/∂t².
  ∇²E = μ₀ε₀∂²E/∂t².
  ∇×(∇×B) = ∇(∇∙B) - ∇²B = μ₀ε₀(∂/∂ t)(∇×E) = -μ₀ε₀∂²B/∂t².
  ∇²B = μ₀ε₀∂²B/∂t².
  μ₀ε₀ = 1/c².
  (b)  Each Cartesian component of E and B satisfies the 3-dimensional, homogeneous wave equation.
  Sinusoidal plane wave solutions E(r,t) = E₀ exp(i(k_i∙r - ωt)),  B(r,t) = B₀ exp(i(k_i∙r - ωt)) exist.
  ∇∙E = ∂E_x/∂x + ∂E_y/∂y +∂E_z/∂z = ik∙E  = 0
  ∇∙E = 0 requires that E∙k = 0 for radiation fields, i.e. that E is perpendicular to k.
  Similarly, ∇∙B = 0 requires that B∙k = 0 for radiation fields.
  ∇×E = -∂B/∂t requires that ik×E = iωB,  i.e. B is perpendicular to E and k.
  (c) B = (k/ω)E = E/c.

Problem:

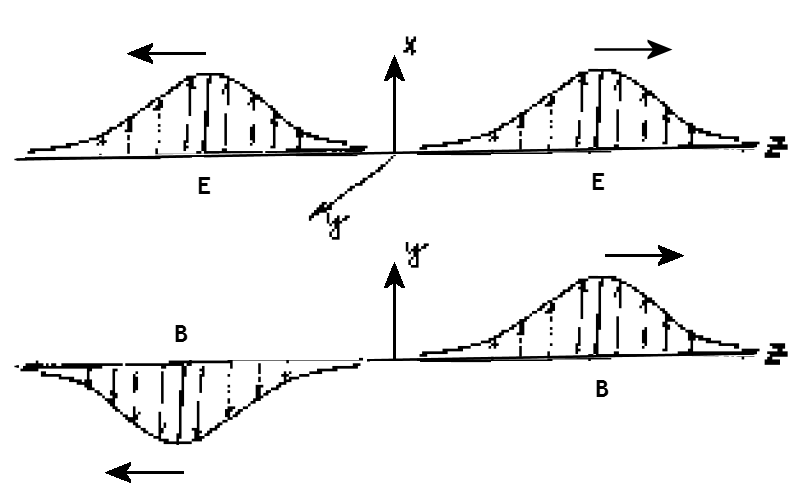
A time-dependent, vacuum electromagnetic field in three dimensions (x, y, z) at time, t = 0, is shown in the figure.

It has the following form:
E(r, t = 0) = i  E₀exp(-(z/a)²),  B(r, t = 0) = 0.
(a) Evaluate ∂E/∂t at t = 0.
(b) Evaluate ∂B/∂t at t = 0.
(c) Evaluate ∂²E/∂t² at t = 0 and show that E satisfies the wave equation at t = 0.
(d) What are the values of the fields E(r, t ) and B(r, t ) for a general time t, satisfying the inequality ct/a >> 1.
(e) Sketch in a single diagram the fields found in (d).

Solution:

• Concepts:
  Maxwell's equations
• Reasoning:
  Maxwell's equations relate partial derivatives of E and B with respect to space and time and yield the wave equation
• Details of the calculation:
  ∇∙E = 0,  ∇∙B = 0,
  ∇×E = -∂B/∂t,  ∇×B = (1/c²)∂E/∂t
  (a)  Here E(r, t = 0) = i  E₀exp(-(z/a)²),  B(r, t = 0) = 0.
  At t = 0, ∇×B = (1/c²)∂E/∂t = 0, ∂E/∂t = 0.
  (b)  ∇×E = -∂B/∂t = j (∂E_x/∂z),  ∂B/∂t = j (2z/a²) E₀exp(-(z/a)²).
  (c)  ∂²E/∂t² = c²(∂/∂t)(∇×B)  = c²∇×∂B/∂t.
  At t = 0, ∂²E/∂t² = c²∇×(j (2z/a²) E₀exp(-(z/a)²)).
  ∂²E/∂t² = -c²i (∂/∂z)[(2z/a²) E₀exp(-(z/a)²))] = c²i (∂²/∂z²)[E₀exp(-(z/a)²))] = c²∇²E.
  ∇²E - (1/c²)∂²E/∂t² = 0.
  E satisfies the wave equation at t = 0.
  (d)  The given E can only satisfy the wave equation if it is the sum of a function of z - ct and another function of c + zt.  The same holds for B.
  E(r, t) = i [(E₀/2)(exp(-((z-  ct)/a)²) + exp(-((z + ct)/a)²)],
  B(r, t) = j [(E₀/(2c))(exp(-((z - ct)/a)²) - exp(-((z + ct)/a)²)].
  (e)  We have two Gaussian-shaped electromagnetic pulses one traveling into the positive and one in the negative z-direction.
  

Problem:

In unbounded free space the electric and magnetic fields satisfy

∇∙E = ∇∙B = 0,  ∇×E = -∂B/∂t,  ∇×B = (1/c²)∂E/∂t,

and therefore  the homogeneous wave equation.
Assume that at t = 0 E(r, t = 0) = j f(x) and B(r, t = 0) = 0.
Find E(r,t) and B(r, t) for t > 0.

Solution:

• Concepts:
  Maxwell's equations
• Reasoning:
  Maxwell's equations relate partial derivatives of E and B with respect to space and time and yield the wave equation
• Details of the calculation:
  E and B must satisfy the homogeneous wave equation, ∇²E = (1/c²)∂²E/∂t².
  We have E ⊥ B,  E, B ⊥ direction of propagation, E×B pointing in the direction of propagation.
  E is perpendicular to the xz-plane.  ∇×E = k ∂E_y/∂x =  k ∂f(x)/∂x.
  B points in the ±z-direction.  The EM wave therefore propagates along the ±x-direction.
  The given E can only satisfy the wave equation if it is the sum of a function of x - ct and another function of x + ct.  The same holds for B.
  E(r, t) = j ½(f(x - ct) + f(x + ct)),
  B(r, t) = k ½(f(x +  ct) - f(x + ct)).
  We have two electromagnetic pulses, one traveling into the positive and one in the negative x-direction.