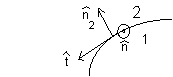Scalar and vector potentials

Problem:

(a)  Write down Maxwell's equations in free space and in the presence of the current density j(r,t) and charge density ρ(r,t).  Introduce the electromagnetic potentials and derive the differential equation that they satisfy.
(b)  State the Lorentz condition and show the simplification found thereby.
(c)  Define a gauge transformation and describe its effect on the electromagnetic fields.

Solution:

• Concepts:
  Maxwell's equations, scalar and vector potential, the Lorentz condition, gauge transformations
• Reasoning:
  Starting from Maxwell's equations, we are asked to introduce the electromagnetic potentials and derive the differential equation that they satisfy.
• Details of the calculation:
  (a)  Maxwell's equations in SI units are
  ∇∙E = ρ/ε₀,  ∇×E = -∂B/∂t,  ∇∙B = 0,  ∇×B = μ₀j + (1/c²)∂E/∂t.
  We find
  ∇∙B = 0 --> B = ∇×A,   ∇×(E + ∂A/∂t) = 0 --> -> E + ∂A/∂t = -∇Φ.
  Therefore
  ∇²Φ + ∂∇∙A/∂t = -ρ/ε₀,  and  ∇×(∇×A) - (1/c²)∂(-∇Φ - ∂A/∂t)/∂t = μ₀j.
  are the differential equations satisfied by the potentials.
  Using
  ∇×(∇×A) = ∇(∇∙A) - ∇²A
  we write
  ∇²A - (1/c²)∂²A/∂t² - ∇(∇∙A +(1/c²)∂Φ/∂t ) = -μ₀j.
  
  (b)  Lorentz condition:  ∇∙A = -(1/c²)∂Φ/∂t  (We pick an expression for ∇∙A.)
  Simplification: 
  ∇²Φ - (1/c²)∂²Φ/∂t² = -ρ/ε₀,    ∇²A - (1/c²)∂²A/∂t² = -μ₀j.
  are now the differential equations satisfied by the potentials.
  Φ, A_x, A_y, A_z now satisfy the inhomogeneous wave equation.
  (c)  A and Φ are not unique.
  A --> A + ∇ψ,  Φ --> Φ - ∂ψ/∂t is called a gauge transformation.
  E and B are invariant under such a transformation.

Problem:

In the derivation of the wave equations for A and Φ from Maxwell's equations in a vacuum, one gets at one stage
∇²A - (1/c²)∂²A/∂t² - ∇(∇∙A +(1/c²)∂Φ/∂t ) = -μ₀j.
and
∇²Φ + ∂∇∙A/∂t = -ρ/ε₀.
This is made solvable by use of a gauge choice, using the fact that physics is invariant under a gauge transformation.  Write down the Lorentz gauge condition and the resulting PDE's for Φ and A.

Solution:

• Concepts:
  Maxwell's equations, scalar and vector potential, the Lorentz condition, gauge transformations
• Reasoning:
  We are asked to use the Lorentz condition to simplify the given PDE's.
• Details of the calculation:
  Lorentz condition:  ∇∙A = -(1/c²)∂Φ/∂t  (we pick an expression for ∇∙A.)
  Simplification:
  ∇²Φ - (1/c²)∂²Φ/∂t² = -ρ/ε₀,    ∇²A - (1/c²)∂²A/∂t² = -μ₀j.
  are now the differential equations satisfied by the potentials.
  Φ, A_x, A_y, A_z now satisfy the inhomogeneous wave equation.
  A and Φ are not unique.
  A --> A + ∇ψ,  Φ --> Φ - ∂ψ/∂t is called a gauge transformation.
  E and B are invariant under such a transformation.

Problem:

(a)  Find the magnetic field associated with the potential A(r,t) = (b/2)n×r.
(b)  Find the charge and current distributions that would lead to
A(r,t) = (bt/r³)r,  Φ(r,t) = 0.
(c)  Determine the charge distribution that will give rise to the potential
Φ(r,t) = W₀exp(-αr)/r.

Solution:

• Concepts:
  Maxwell's equations, scalar and vector potential, Gauss' law
• Reasoning:
  E = -∂A/∂t - ∇Φ, B = ∇×A, (SI units).
  Given the potentials we are asked to find the fields.
• Details of the calculation:
  (a)  A_x = (b/2)(n_yz - n_zy), A_y = (b/2)(n_zx - n_xz), A_z = (b/2)(n_xy - n_yx).
  B_x = ∂A_z/∂y - ∂A_y/∂z = (b/2)(n_x + n_x) = bn_x, B_y = bn_y,  B_z = bn_z.
  B = bn, a uniform field in the n direction of strength b.
  (b)  E = -∂A/∂t - ∇Φ = (b/r³)r.
  This is the field of a point charge at the origin with q = 4πε₀b.
  B = ∇×A = 0, ∇×B = μ₀j + (1/c²)∂E/∂t = 0, this implies that j = 0.
  (c)  E(r) = -∇Φ(r) = W₀(α exp(-αr)/r + exp(-αr)/r²)(r/r).
  E(r) is radial, we have a spherically symmetric charge distribution.
  ∫_{surface of sphere of radius R}E∙ndA = E(R)4πR² = 4πW₀(1 + αR)exp(-αR) = Q_inside/ε₀.
  As r --> 0, Q_inside --> 4πε₀W₀, there is a point charge at the origin.
  For r ≠ 0, ρ(r) = -ε₀∇²Φ(r) = -ε₀∇²(W₀exp(-αr)/r)
  = -ε₀W₀(1/r²)(∂/∂r)[r²(∂/∂r)(exp(-αr)/r)].
  ρ(r) = -ε₀W₀α²exp(-αr)/r.
  Therefore ρ(r) = ε₀W₀(4πδ(r) - α²exp(-αr)/r).

Problem:

(a)  State Maxwell's equations and prove that they are satisfied by E = -∂A/∂t, B = ∇×A,  provided ∇∙A = 0, ∇²A = (1/c²)∂²A/∂t².
(b)  Derive E and B when A = i a cos(k(z - ct))+ + j b sin(k(z - ct)).
(c)  Verify that E and B are orthogonal and their directions rotate about the z-axis with  frequency kc/(2π).

Solution:

• Concepts:
  Maxwell's equations, E = -∂A/∂t - ∇Φ,  B = ∇×A
• Reasoning:
  Given ∇∙A = 0, ∇²A - (1/c²)∂²A/∂t² = 0,  we are supposed to show that E = -∂A/∂t, B = ∇×A satisfy Maxwell's equations.
• Details of the calculation:
  (a)  Maxwell's equations in SI units are
  ∇∙E = ρ/ε₀,  ∇×E = -∂B/∂t,  ∇∙B = 0,  ∇×B = μ₀j + (1/c²)∂E/∂t
  Assume that E = -∂A/∂t, B = ∇×A.
  ∇∙B = 0 automatically and ∇∙E = 0 from ∇∙A = 0, which implies that ρ = 0.
  ∇×E = -∂/∂t(∇×A) = -∂B/∂t.
  Only the ∇×B equation remains.
  ∇×B = ∇×(∇×A) = ∇(∇∙A) - ∇²A =  -∇²A.
  Given: ∇²A - (1/c²)∂²A/∂t² = 0
  Therefore ∇×B = -(1/c²)∂²A/∂t² = (1/c²)∂E/∂t, which is the remaining equation.  It implies that j = 0.
  In free space with ρ = 0 and  j = 0 Maxwell's equations are correctly obtained from a single vector potential A satisfying
  ∇∙A = 0, ∇²A - (1/c²)∂²A/∂t² = 0,  Φ = 0.
  (b)  When A = i a cos(k(z - ct)) + j b sin(k(z - ct)), we have
  E = -∂A/∂t = -i akc sin(k(z - ct)) + j bkc cos(k(z - ct)).
  B = ∇×A = -i kb cos(k(z - ct)) - j ak sin(k(z - ct)).
  (c)  E∙B = akc sin(k(z - ct)) kb cos(k(z - ct)) - bkc cos(k(z - ct)) ak sin(k(z - ct)) = 0.
  E and B are orthogonal.
  At a given position along the z-axis, say z = 0,  E =  i akc sin(kct) + j bkc cos(kct) =  i akc sin(ωt) + j bkc cos(ωt).
  The x and y coordinates oscillate 90^o out of phase with angular frequency ω = kc, the tip of E  moves clockwise on an ellipse.
  B = -i kb cos(ωt) + j ak sin(ωt), the tip of B  moves clockwise on an ellipse.

Problem:

(a)  A point charge q rests at the origin.  
A natural choice of potentials for this static problem is V(r,t) = q/(4πε₀r), A(r,t) = 0.
Consider the gauge transformation with λ(r,t) = qt/(4πε₀r) + k/r³,
where k is a constant.
Calculate the transformed potentials and fields.   Discuss the result.
(b)  Find E and B given the potentials  A(ρ,φ,z) = -k C ln(ρ²)/(4π),  V = 0.
Which charge or current distributions produce these fields?   Can you find a gauge transformation which leaves the transformed vector potential  A(ρ,φ,z) = 0?

Solution:

• Concepts:
  Gauge transformations
• Reasoning:
  A and Φ are not unique.
  A --> A + ∇λ, V --> V - ∂λ/∂t is called a gauge transformation.
• Details of the calculation:
  (a) Transformed potentials:
  A_r(r,t)  = ∂λ/∂r = -qt/(4πε₀r²) - 3k/r⁴.  The other components of A are zero.
  V(r,t) = -q/(4πε₀r)  - q/(4πε₀r)  = 0.
  E = -∂A/∂t - ∇V, B = ∇×A, (SI units).
  Transformed fields:
  E_r = -∂A_r/∂t = q/(4πε₀r²), the other components of E are zero.
  B = ∇×A = 0 since A is irrotational.  It has only a radial component which does not depend on θ and φ.
  E and B are invariant under a gauge transformation.
  (b) B = ∇×A = -∂A_z/∂ρ (φ/φ) = C/(2πρ) (φ/φ),  E = 0.
  This is the magnetic field produced by a current I = C/μ₀ in an infinitely long, straight wire.  No free charges are present.
  A gauge transformation leaving A' = 0 does not exist since B = ∇×A is not equal to zero.

Problem:

(a)  Write down expressions for the electric field E and the magnetic field B in terms of the scalar potential Φ and the vector potential A.
(b)  Given Φ = 0 and  A = k [μ₀α/(4c)](ct -|x|)² for |x| < ct, A = 0 for |x| > ct, find E and B.
(c)  Write down the boundary conditions for the normal component of E and the tangential component of B at the x = 0 interface.
(d)  Find the surface charge density and the surface current density at the x = 0 interface.  (Assume media with ε₀ and μ₀ on both sides of the interface.)

Solution:

• Concepts:
  Maxwell's equations, scalar and vector potential
• Reasoning:
  We are supposed to write down E and B in terms of the scalar and vector potential.
• Details of the calculation:
  (a)  E = -∂A/∂t - ∇Φ, B = ∇×A
  (b)  E = -k [μ₀α/2](ct -|x|),  B = ±j [μ₀α/(2c)](ct -|x|),  It  x > 0 B points into the y-direction, if x < 0 B points into the -y-direction
  (c and d)
  
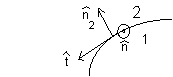
  (E₂ - E₁)∙n₂ = σ/ε₀,,  E is continuous at x = 0, there is no surface charge density.
  
  (B₂ - B₁)∙t = μ₀k∙n, B is discontinuous at x = 0, k_surface = -αt k.

Problem:

Show that in free space with ρ = 0 and  j = 0 Maxwell's equations are correctly obtained from a single vector potential A satisfying

∇∙A = 0, ∇²A - (1/c²)∂²A/∂t² = 0,  Φ = 0.

Solution:

• Concepts:
  Maxwell's equations, E = -∂A/∂t - ∇Φ, B = ∇×A
• Reasoning:
  Given ∇∙A = 0, ∇²A - (1/c²)∂²A/∂t² = 0,  Φ = 0, we are supposed to obtain Maxwell's equations.
• Details of the calculation:
  Φ = 0, therefore E = -∂A/∂t, B = ∇×A.
  ∇∙B = 0 automatically and ∇∙E = 0 from ∇∙A = 0.
  ∇×E = -∂/∂t(∇×A) = -∂B/∂t.
  Only the ∇×B equation remains.
  ∇×B = ∇×(∇×A) = ∇(∇∙A) - ∇²A =  -∇²A.
  Given: ∇²A - (1/c²)∂²A/∂t² = 0.
  Therefore ∇×B = -(1/c²)∂²A/∂t² = (1/c²)∂E/∂t, which is the remaining equation.

Problem:

(a)  Consider the following vector potential A:
A_x = 0,  A_y = bx,  A_z = 0. 
Find the corresponding magnetic field.
(b)  Consider the following vector potential A':
A'_x = -by,  A'_y = 0,  A'_z = 0. 
Find the corresponding magnetic field.
(c)  A' = A + ∇f(x, y,z).  Find f.
(d)  The Lagrangian of a particle with mass m and charge q moving in the presence of a magnetic field is
L = ½ mv² + qv∙A.
Using the vector potential from part (a) or part (b), write down Lagrange's equations of motion, the Hamiltonian, and Hamilton's equations of motion.
(e)  Solve the equations of motion.

Solution:

• Concepts:
  The vector potential
• Reasoning:
  The vector potential is not unique.  It enters into the Lagrangian, but the equations of motion do not depend on the gauge.
• Details of the calculation:
  (a)  B = ∇×A = b k.
  (b)  B = ∇×A' = b k.
  (c)  ∂f/∂x = -by,  ∂f/∂y = -bx,  ∂f/∂z = 0.
  f = -byx + constant.
  (d)  Using the vector potential from part (a): 
  L = ½ m(v_x² + v_y² + v_z²) + qv_ybx.
  ∂L/∂v_x = mv_x = p_x  ∂L/∂v_y = mv_v + qbx = p_y = constant,  ∂L/∂v_z = mv_z = p_z = constant.
  Lagrange's equations of motion:
  p_z = mv_z = constant, dv_z /dt = a_z = 0.
  p_y = mv_v + qbx = constant, dv_y /dt = a_y = -qbv_x/m.
  d/dt(∂L/∂v_x) - ∂L/∂x = 0,  a_x = qbv_y/m.
  H(x,p) = p_xv_x + p_yv_y + p_zv_z - L
  = p_x²/m + p_y(p_y - qbx)/m + p_z²/m - ½p_x²/m - ½(p_y -qbx)²/m - ½p_z²/m - qv_ybx
  = ½p_x²/m + ½(p_y - qbx)²/m + ½p_z²/m.
  Note: p is the canonical, not the mechanical momentum.
  Hamilton's equations of motion:  ∂H/∂p_x = dx/dt,  ∂H/∂x = -dp_x/dt, similar for the other components.
  v_x = p_x/m,  v_y = (p_y - qbx)/m,  v_z = p_z/m,
  dp_x/dt = qb(p_y - qbx)/m,  dp_y/dt = 0,  dp_z/dt = 0.
  This yields a_z = 0,  a_y = -qbv_x,  a_x = qb(p_y  - qbx)/m² = qbv_y/m.
  (e) a_z = 0,  v_z = v_z0,  z = z₀ + v_z0t.
  a_y = -qbv_x,  a_x = qbv_y/m.
  x = Acos(ωt + φ) + x₀,  y = Asin(ωt + φ) + y₀,  v_x = -ωAsin(ωt + φ),  v_y = ωAcos(ωt + φ),
  a_x = -ω²Acos(ωt + φ) = ωv_y,  a_y = -ω²Asin(ωt + φ) = ωv_x, ω = qb/m.
  The initial conditions determine x₀, y₀, A and φ.