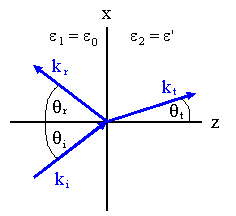Plane waves in dielectrics, dielectric-dielectric boundaries

Problem:

In a purely classical model we consider a dielectric medium as a collection of uncoupled classical harmonic oscillators.  Assume that each oscillator consists of an electron connected to a fixed ion by a harmonic spring with frequency ω₀.
(a)  Write down and solve the equation of motion for the electron when a monochromatic electric field with frequency ω is applied.
(b)  For an electron density n, calculate the electric polarization and the dielectric constant ε(ω).
(c)  For a free electron gas, at what frequency is ε = 0?  What is the physical significance of this frequency?

Solution:

• Concepts:
  The driven harmonic oscillator, polarization, the plasma frequency
• Reasoning:
  We model a medium interacting with an electromagnetic as a collection of driven harmonic oscillators.
• Details of the calculation:
  (a)  Let E = E₀ exp(-iωt).
  The electric field and the spring exert a force on the electron.  The total force is
  F = -q_e E - mω₀²r =  md²r/dt².
  To solve this differential equation try a solution of the form
  r = r₀ exp(-iωt).  This yields
  r₀ = -(q_eE₀/m)/(ω₀² - ω²).
  (b)  The induced dipole moment is p = -q_er = (q_e²E₀/m)/(ω₀² - ω²) exp(-iωt).
  Polarization = dipole moment per unit volume
  P = np = n(q_e²E/m)/(ω₀² - ω²) = ε₀χ_eE.
  ε(ω) = ε₀(1 + χ_e) = ε₀ + n(q_e²/m)/(ω₀² - ω²).
  (c)  For a free electron ω₀ = 0.
  We then have ε(ω) = ε₀ - nq_e²/(m ω²) = ε₀(1 - nq_e²/(ε₀m ω²)) = ε₀(1 - ω_p²/ω²).
  When ω = ω_p the ε(ω) = 0.  ω_p = (nq_e²/(ε₀m))^½ is called the plasma frequency.  The plasma is opaque to EM waves with frequencies less than ω_p and transparent to EM waves with frequencies greater than ω_p.

Dielectric-dielectric boundaries

Problem:

A plane electromagnetic wave is incident normally from vacuum onto a plane (uniform, isotropic, non permeable, loss-less) dielectric interface.
(a)  Formulate the problem in terms of Maxwell's equations with the appropriate boundary conditions.
(b)  Determine the amplitude of reflected and transmitted waves.
(c)  Determine (i) the ratio of the reflected to the incident intensity, and (ii) the ratio of the transmitted to the incident intensity.

Solution:

• Concepts:
  Maxwell's equations, boundary conditions for the electric and magnetic fields
• Reasoning:
  The intensities of the reflected and transmitted waves are proportional to the squares of the corresponding electric field amplitudes.  We find the ratio of these amplitudes to the incident amplitude by applying boundary conditions.
• Details of the calculation:
  (a)  Maxwell's equations in an ideal linear, isotropic, homogeneous dielectric medium are
  ∇∙E = ρ_f/ε,  ∇×E = -∂B/∂t,  ∇∙B = 0,  ∇×B = μj_f + εμ∂E/∂t.
  You may replace E by D/ε and B by μH.
  Assume ρ_f and j_f are zero in the medium.  Then
  ∇×(∇×E) = ∇(∇∙E) - ∇²E = -(∂/∂ t)(∇×B) = -με∂²E/∂t².
  ∇²E = με∂²E/∂t².
  ∇×(∇×B) = ∇(∇∙B) - ∇²B = με(∂/∂ t)(∇×E) = -με∂²B/∂t².
  ∇²B = με∂²B/∂t².
  Plane wave solutions E = E((k/k)∙r - vt).  B = B((k/k)∙r - vt) exist.  (v = (με)^-½).
  We have  E ⊥ B.  E ⊥ k.  B ⊥ k.  B = (με)^½(k/k)×E.
  k² = μεω²   (SI units).
  Sinusoidal plane waves are of the form  E = E₀e^{i(k∙r - ωt)}.  B = B₀e^{i(k∙r - ωt)}.
  Maxwell's equation yield the boundary conditions
   

  (SI units)

  (D2 - D1)∙n2 = σf

  (B2 - B1)∙n2 = 0

  (E2 - E1)∙t = 0

  (H2 - H1)∙t = kf∙n

  At a dielectric-dielectric interface σ_f and k_f are zero

  
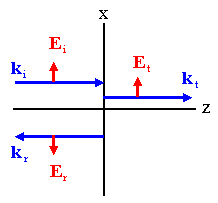
  If we set up the problem as shown in the figure above the boundary conditions yield
  (E₂ - E₁)∙t = 0.  (E₂ - E₁)∙(x/x) = 0.  E_i - E_r = E_t.
  (H₂ - H₁)∙t = k_f∙n, (H₂ - H₁)∙(y/y) = 0, there are no free surface currents.
  H₂ = B₂/μ₂.  H₁ = B₁/μ₁.
  B = (1/v)(k/k)×E.  B_i = (y/y)E_i(n₁/c), B_r = (y/y)E_i(n₁/c), B_t = (y/y)E_t(n₂/c).
  (n₁/μ₁)(E_i + E_r)  = (n₂/μ₂)E_t.
  (b) (n₁/μ₁)(E_i + E_r)  = (n₂/μ₂)(E_i - E_r).
  E_r/E_i = (n₂μ₁ - n₁μ₂)/(n₂μ₁ + n₁μ₂) = r₁₂  is the reflection coefficient.
  Let β = (μ₁n₂/μ₂n₁) = (μ₁/μ₂)(ε₂μ₂)^½/(ε₁μ₁)^½ = (ε₂μ₁)^½/(ε₁μ₂)^½.
  Then we can write
  (β - 1)/(β + 1) = r₁₂.
  
  (n₁/μ₁)(2E_i - E_t)  = (n₂/μ₂)E_t.
  E_t/E_i = 2n₁μ₂/(n₁μ₂ + n₂μ₁) = t₁₂  is the transmission coefficient.
  We can write
   2/(1 + β) = t₁₂.
  (c) The reflectance is  R = <S_r>/<S_i> = |r₁₂|²,
  and the transmittance is  T = <S_t>∙n/<S_i>∙n where n is a unit vector normal to the interface.
  T = <S_t>/<S_i> = (μ₁n₂/μ₂n₁)|t₁₂|².  R + T = 1.
  [<S> = (|E₀²|/2)(ε/μ)^½] =  (|E₀²|/2)(n/(cμ).]

Problem:

A plane electromagnetic wave is incident upon a a plane dielectric-dielectric interface as shown below.

The polarization is normal to the plane defined by the incident, reflected, and transmitted wave vector.
(a)  Show that Snell's law and the law of reflection result from application of the appropriate boundary conditions.
(b)  Show that the reflection coefficient is given by E_r/E_i = sin(θ_t - θ_i)/sin(θ_t + θ_i).

Solution:

• Concepts:
  Maxwell's equations, boundary conditions for the electric and magnetic fields
• Reasoning:
  The intensities of the reflected and transmitted waves are proportional to the squares of the corresponding electric field amplitudes.  We find the ratio of these amplitudes to the incident amplitude by applying boundary conditions.
• Details of the calculation:
  (a)  The y-direction is the direction of the polarization, we have s-polarization.
  E_i(r,t) = j E_i exp(i(k_i∙r - ωt)). 
  E_r(r,t) = j E_r exp(i(k_r∙r - ωt)). 
  E_t(r,t) = j E_t exp(i(k_t∙r - ωt)).
  The tangential component of E is continuous across the boundary.  The y-direction is tangential to the interface.  Therefore E_i exp(i(k_i∙r)) + E_r exp(i(k_r∙r)) = E_t exp(i(k_t∙r)) for all r in the z = 0 plane.
  This is only possible if k_i∙r = k_r∙r = k_t∙r for all r in the z = 0 plane.
  Let r = i, then k_ix = k_rx = k_tx.  or   k_isin(θ_i) = k_rsin(θ_r) = k_tsin(θ_t).
  k_i = k_r = (με)^½ω = n₁ω/c.  k_t = (με')^½ω = n₂ω/c.  Therefore
  n₁sin(θ_i) = n₁sin(θ_r) = n₂sin(θ_t).
  This implies θ_i = θ_r (law of reflection) and n₁sin(θ_r) = n₂sin(θ_t) (Snell's law).
  (b)  The tangential component of H = B/μ is continuous across the boundary.  The x-direction is tangential to the interface.  Since μ is the same on both sides of the interface, the tangential component of B is continuous across the boundary.
  B_i = k_i×E_i/ω.  B_i∙i = (1/ω)(k_i×E_i)∙i = (1/ω)(E_i×i)∙k_i = -(1/ω)E_ik_iz = -(1/ω)E_ik_icos(θ_i).
  Similarly B_r∙i = (1/ω)E_rk_rcos(θ_r).  B_t∙i = -(1/ω)E_tk_tcos(θ_t).
  We then have E_ik_icos(θ_i) - E_rk_rcos(θ_r) = E_tk_tcos(θ_t),
  or  n₁E_icos(θ_i) - n₁E_rcos(θ_r) = n₂E_tcos(θ_t).
  Combining this equation with E_i + E_r = E_t and θ_i = θ_r yields
  E_r/E_i = (n₁cosθ_i - n₂cosθ_t)/(n₁cosθ_i + n₂cosθ_t)
  = (cosθ_i - (sinθ_i/sinθ_t)cosθ_t)/(cosθ_i + (sinθ_i/sinθ_t)cosθ_t)
  = (1 - (tanθ_i/tanθ_t))/(1 + (tanθ_i/tanθ_t))
  = (tanθ_t - tanθ_i)/(tanθ_t + tanθ_i)
  = sin(θ_t - θ_i)/sin(θ_t + θ_i).
  [sin(a - b)/sin(a + b) = (sina cosb - cosa sinb)/(sina cosb + cosa sinb)
  = sina cosb/(sina cosb + cosa sinb) - cosa sinb/(sina cosb - cosa sinb)
  = 1/(1 + tanb/tana) - 1/(1 + tana/tanb)
  = (tana - tanb)/(tana + tanb)].

Problem:

Fresnel's reflectance formulas are given by

R = |sin(θ_i - θ_r)/sin(θ_i + θ_r)|²   or   R = |tan(θ_i - θ_r)/tan(θ_i + θ_r)|²

depending on the polarization of the incident wave with respect to the plane of incidence, and with θ_i and θ_r the angles of incidence and refraction, respectively.
(a)  Specify the boundary conditions across an interface.
(b)  For simplicity assume μ₁ = μ₂ = μ₀, ε₁ = ε₀, ε₂ = ε, and derive the reflectance formulas.
(c)  For polarization parallel to the plane of incidence, find the Brewster angle for an index of refraction of n₂ = 1.50, and comment on the polarization of the reflected radiation for a wave of mixed polarization incident on a plane interface at the Brewster angle.

Solution:

• Concepts:
  Maxwell's equations, boundary conditions for the electric and magnetic fields
• Reasoning:
  The intensities of the reflected and transmitted waves are proportional to the squares of the corresponding electric field amplitudes.  We find the ratio of these amplitudes to the incident amplitude by applying boundary conditions.
• Details of the calculation:
  (a)  At a dielectric-dielectric interface Maxwell's equation yield the boundary conditions
   

  (SI units)

  (D2 - D1)∙n2 = σf

  (B2 - B1)∙n2 = 0

  (E2 - E1)∙t = 0

  (H2 - H1)∙t = kf∙n

  (b)  In the figure below, the y-direction is the direction of the polarization for s-polarization.
  
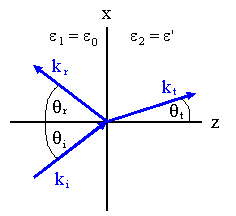
  E_i(r,t) = j E_i exp(i(k_i∙r - ωt)). 
  E_r(r,t) = j E_r exp(i(k_r∙r - ωt)). 
  E_t(r,t) = j E_t exp(i(k_t∙r - ωt)).
  The tangential component of E is continuous across the boundary.
  The y-direction is tangential to the interface.
  Therefore E_i exp(i(k_i∙r)) + E_r exp(i(k_r∙r)) = E_t exp(i(k_t∙r)) for all r in the z = 0 plane.
  This is only possible if k_i∙r = k_r∙r = k_t∙r for all r in the z = 0 plane.
  Let r = i, then k_ix = k_rx = k_tx,   or   k_isin(θ_i) = k_rsin(θ_r) = k_tsin(θ_t).
  k_i = k_r = (μ₀ε₀)^½ω = ω/c.  k_t = (μ₀ε')^½ω = n₂ω/c.  Therefore
  sin(θ_i) = sin(θ_r) = n₂sin(θ_t).
  This implies θ_i = θ_r (law of reflection) and sin(θ_r) = n₂sin(θ_t) (Snell's law) for s-polarization.
  
  The tangential component of B = μ₀H is continuous across the boundary.  The x-direction is tangential to the interface.
  B = k×E/ω,  B_i∙i = (1/ω)(k_i×E_i)∙i = (1/ω)(E_i × i)∙k_i = -(1/ω)E_ik_iz = -(1/ω)E_ik_icos(θ_i).
  Similarly B_r∙i = (1/ω)E_rk_rcos(θ_r),  B_t∙i = -(1/ω)E_tk_tcos(θ_t).
  We then have E_ik_icos(θ_i) - E_rk_rcos(θ_r) = E_tk_tcos(θ_t),
  or  E_icos(θ_i) - E_rcos(θ_r) = n₂E_tcos(θ_t).
  Combining this equation with E_i + E_r = E_t and θ_i = θ_r from above yields
  E_r/E_i = (cosθ_i - n₂cosθ_t)/(cosθ_i + n₂cosθ_t)
  = (cosθ_i - (sinθ_i/sinθ_t)cosθ_t)/(cosθ_i + (sinθ_i/sinθ_t)cosθ_t)
  = (1 - (tanθ_i/tanθ_t))/(1 + (tanθ_i/tanθ_t))
  = (tanθ_t - tanθ_i)/(tanθ_t + tanθ_i)
  = sin(θ_t - θ_i)/sin(θ_t + θ_i).
  R =|E_r/E_i|² = |sin(θ_t - θ_i)/sin(θ_t + θ_i)|².
  [sin(a - b)/sin(a + b) = (sina cosb - cosa sinb)/(sina cosb + cosa sinb)
  = sina cosb/(sina cosb + cosa sinb) - cosa sinb/(sina cosb - cosa sinb)
  = 1/(1 + tanb/tana) - 1/(1 + tana/tanb)
  = (tana - tanb)/(tana + tanb)].

  In the figure below, the direction of B is tangential to the interface for p-polarization.
  
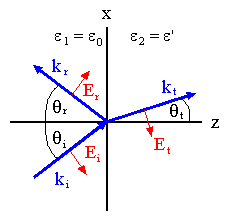
  B_i(r,t) = -j B_i exp(i(k_i∙r - ωt)), 
  B_r(r,t) = -j B_r exp(i(k_r∙r - ωt)), 
  B_t(r,t) = -j B_t exp(i(k_t∙r - ωt)).
  
  The tangential component of E is continuous across the boundary.
  The x-direction is tangential to the interface.
  Therefore the x-component of E is continuous across the boundary.
  E_i exp(i(k_i∙r))cos(θ_i)  - E_r exp(i(k_r∙r))cos(θ_r) = E_t exp(i(k_t∙r))cos(θ_t) for all r in the z = 0 plane.
  This is only possible if k_i∙r = k_r∙r = k_t∙r for all r in the z = 0 plane.
  Let r = i, then k_ix = k_rx = k_tx,   or   k_isin(θ_i) = k_rsin(θ_r) = k_tsin(θ_t).
  k_i = k_r = (μ₀ε₀)^½ω = ω/c.  k_t = (μ₀ε')^½ω = n₂ω/c.  Therefore
  sin(θ_i) = sin(θ_r) = n₂sin(θ_t).
  This implies θ_i = θ_r (law of reflection) and sin(θ_r) = n₂sin(θ_t) (Snell's law) for p-polarization.
  
  The tangential component of B = μH is continuous across the boundary.
  The y-direction is tangential to the interface.
  B_i + B_r = B_t.
  B = k×E/ω,  B_i = (1/ω)E_ik_i, = E_i/c. B_r = (1/ω)E_rk_r = E_r/c, B_t = (1/ω)E_tk_t = n₂E_t/c.
  We then have E_i + E_r = n₂E_t.
  Combining this equation with E_i cos(θ_i)  - E_r cos(θ_r) = E_t cos(θ_t) and θ_i = θ_r  ffom above yields
  E_r/E_i = (n₂cosθ_i - cosθ_t)/(n₂cosθ_i + cosθ_t)
  = ((sinθ_i/sinθ_t)cosθ_i - cosθ_t)/((sinθ_i/sinθ_t)cosθ_i + cosθ_t)
  = (sinθ_icosθ_i - cosθ_tsinθ_t)/(sinθ_icosθ_i + cosθ_tsinθ_t)
  = tan(θ_i - θ_t)/tan(θ_i + θ_t).
  R =|E_r/E_i|² = |tan(θ_i - θ_t)/tan(θ_t + θ_i)|².
  [(sina cosa - cosb sinb)/(sina cosa + cosb sinb)
  = (sina cosa(sin²b + cos²b) - cosb sinb(sin²a + cos²a))/(sina cosa(sin²b + cos²b) + cosb sinb(sin²a + cos²a))
  = (sin(a - b)cos(a + b)/[sin(a + b)cos(a - b)] = tan(a - b)/tan(a  +b)].
  
  (c)  When θ_t + θ_i = п/2, the reflectance is zero for p-polarization.
  This happens when θ_i = θ_B, n₂sinθ_B  = n₂sin((п/2) - θ_B), tanθ_B = n₂/n₁.
  θ_B is called the Brewster angle.
  When θ_i = θ_B, then only light with s-polarization is reflected.  For a wave incident with mixed polarization incident with θ_i = θ_B, the reflected light is polarized.
  With n₁ = 1, n₂ = 1.5 we have θ_B = 56.31^o.

Problem:

An electromagnetic wave passes through a boundary between two media with n₁ = 1 and n₂ = 3 at near-normal incidence of θ_i = 0.5 degree.
(a)  Find the angle θ_t of the transmitted wave
(b)  Find the reflectance and the transmittance for the wave.

Solution:

• Concepts:
  Snell's law, the Fresnel reflection coefficients
• Reasoning:
  Snell's law lets us calculate  and the Fresnel reflection coefficients let us calculate the reflected intensity.
• Details of the calculation:
  (a)  Snell's law:  n₁sinθ₁ = n₂sinθ₂.
  Small angle approximation: n₁θ₁ = n₂θ₂.
  θ₁ = θ_i = 0.5^o =  8.727 mrad.  θ₂ = θ_t = (1/3)*8.727 mrad =  0.1667^o.

  (b)  Fresnel reflection coefficient for p-polarization:  r_12p = tan(θ₁ - θ₂)/tan(θ₁ + θ₂).
  Fresnel reflection coefficient for s-polarization:  r_12s = sin(θ₁ - θ₂)/sin(θ₁ + θ₂).

  Small angle approximation: r₁₂ = (θ₁ - θ₂)/(θ₁ + θ₂), independent of polarization.
  The reflectance R = |r₁₂|² , and the transmittance T = 1 - R.
  r₁₂ = 0.5,  R = 0.25 = 25%,  T = 0.75 = 75%.

Problem:

A beam of light with wavelength 450 nm in vacuum is incident on a prism as shown in the figure, and totally reflected through 90^o.  The index of refraction of the prism is 1.6.

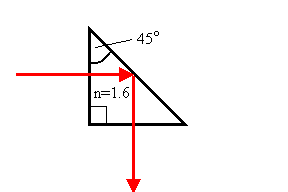
(a)  Compute the distance beyond the long side of the prism at which the electric field strength is reduced to 1/e of its value just at the surface.  Assume the light is polarized so that E is perpendicular to the plane of incidence.
(b)  Is your answer changed if E lies in the plane of incidence?

Solution:

• Concepts:
  Snell's law, total internal reflection, the evanescent wave
• Reasoning:
  If n₂ < n₁ , then for  θ_i > θ_c = sin^-1(n₂/n₁)  we have total internal reflection.  The wave vector k_t then has a component parallel to the interface which is real and a component perpendicular to the interface which is imaginary.  We use Snell's law to calculate the components of the wave vector of the transmitted wave.
• Details of the calculation:
  (a)  Choose a coordinate system.
  
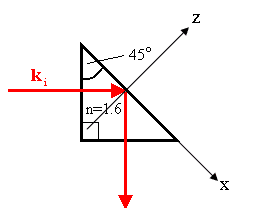
  The interface lies in the x-y plane.  k_i makes an angle of 45_o with the z-axis.  The critical angle for total internal reflection is θ_c = sin^-1(n₂/n₁) = sin^-1(1/1.6) = 38.7^o, so we have total internal reflection.
  n sinθ_i = sinθ_t = 1.1313
  k_tx = k_tsinθ_t.  k_tz = k_tcosθ_t.
  cosθ_t = (1 - sin²θ_t)^½ = i*0.5295.
  k_tcosθ_t = i*0.5295*(2π/450 nm) = iβ.
  E_t = E_0texp(i(k_t∙r - ωt)) = E_0te^-βzexp(i(k_txx - ωt))
  The electric field strength is reduced to 1/e of its value just at the surface when z = 1/β = 135 nm.
  (b)  Polarization does not enter into the above calculation, so the result is independent of the direction of polarization.