Geometrical optics

Snell's law

Problem:

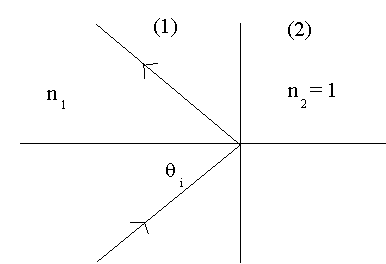
A plane wave is propagating from inside material 1 with index of refraction n₁ toward a plane interface with material 2, as shown.  The index of refraction of material 2 is n₂ = 1.  For angles θ_i > 50^o the wave is totally reflected.
(a)  Find the index of refraction n₁ of material 1.
(b)  For θ_i = 0 find the transmittance T.

Solution:

• Concepts:
  Snell's law: n₁sinθ_i = n₂sinθ_t, total internal reflection, transmission coefficient and transmittance
• Reasoning:
  If n₂ < n₁, then for angles θ_i > sin^-1(n₂/n₁) we have total internal reflection.
  The transmission coefficient for normal incidence is t_12s = t_12p = 2n₁/(n₂ + n₁) if we assume μ₁ = μ₂ = μ₀.
• Details of the calculation:
  (a)  sin(50^o) = 1/n₁.  n₁ = 1.3.
  (b)  t_12s = t_12p = 2n₁/(n₂ + n₁) = 1.13.
  T = <S_t>∙n/<S_i>∙n where n is a unit vector normal to the interface.
  T = (n₂/n₁)|t₁₂|² = 0.986

Problem:

A beam of monochromatic light traveling through air strikes the top of a flat slab of glass at an angle 60^o to the normal, passes through the glass, and emerges from the bottom of the slab.  The glass has a thickness t and a refractive index n = 1.52.

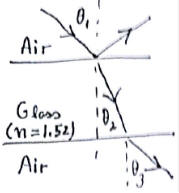
(a)  What is the angle of refraction where the light enters the glass?
(b)  Show that the beam emerging from the glass is parallel to the incident beam.

Solution:

• Concepts:
  Snell's law
• Reasoning:
  We apply Snell's law at both interfaces.
• Details of the calculation:
  (a)  n₁ sinθ₁ = n₂ sinθ₂, 
  sinθ₂ = (n₁/n₂) sinθ₁ = (1/1.52) sin 60^o = 0.569
  θ₂ = 34.7^o
  (b)  Substitute from part (a) and use n₁ = n₃.
  n₂ sinθ₂ = n₃ sinθ₃,
  n₂ (n₁/n₂) sinθ₁ = n₁ sinθ₃,  sinθ₁ = sinθ₃,  θ₁ = θ₃

Problem:

A small source of light is mounted inside a cylindrical container of height h.  The bottom of the container is covered with a mirror.  Initially, the container is empty.  Then a clear liquid with the index of refraction n is slowly poured into the container.  The level of liquid rises steadily, reaching the top of the container in time t.  Find the speed of the image of the source during this process.

Solution:

• Concepts:
  Reflection and refraction
• Reasoning:
  The light is refracted at at the boundary between liquid and air and reflected at the bottom of the container.
  Ignore reflections from the surface of the liquid.
• Details of the calculation:
  Let the source be located a distance d above the bottom of the container, d < h.
  The height of the liquid at time t' is h' = (h/t)t'.
  Trace two rays leaving the source, one vertical, and one making a small angle θ with the vertical.  Their (virtual) intersection marks the image position
  (a)  Assume h' < d.
  
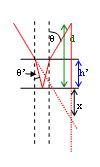
  Applying the law of refraction sinθ = nsinθ' in the small angle approximation we have θ = nθ'. 
  Trigonometry then yields (d - h')θ + 2h'θ/n = (x + h')θ or x = d - 2h' + 2h'/n.
  Here x is the distance of the image below the bottom of the container.
  dx/dt' = -2h/t + 2h/(tn) = -(2h/t)(1 - 1/n).
  So x is decreasing at a steady rate, the image of the source is moving up with speed
  v = (2h/t)(1 - 1/n).
  
  (b)  Assume h' > d < h.
  
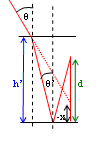
  In the small angle approximation trigonometry yields
  dθ/n + h'θ/n = (x + h')θ.
  Note: x is negative if the image position is above the bottom of the container.
  x = d/n + h'/n - h'.  dx/dt = h/(nt) - h/t = -(h/t)(1 - 1/n)
  So x is still decreasing, the image of the source is now moving up with speed
  v = (h/t)(1 - 1/n).

Problem:

A parallel beam of monochromatic light strikes a transparent prism.  The cross section of the prism is a regular hexagon.  The beam is parallel to the "top" and "bottom" faces of the prism, and points A and B in the diagram are the midpoints of the corresponding edges.

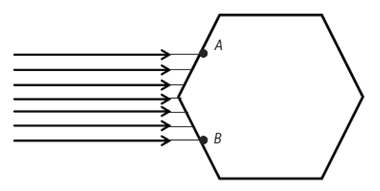
After the refraction, two separate parallel beams of light emerge from the prism. What is the minimum index of refraction of the material of the prism that allows such an effect?

Solution:

• Concepts:
  Snell's law
• Reasoning:
  Consider the diagram of the hexagonal prism below, along with the part of the light beam entering between points C and A

  

  Since the side containing A and C is parallel to the side containing A' and C', the beam emerging from the strip A'C' will be parallel to the beam entering the strip AC.  By symmetry, another parallel beam exits from the side just above point A'.  The diagram is for the minimum index of refraction needed to have two parallel beams.  In the diagram the separation between the beams is zero.  A larger index moves points A' and C' down their side, creating a "blank" region between the two parallel beams.

• Details of the calculation:
  Suppose that the hexagon has side length L.  The distance from midpoint A to midpoint C' is
  2L cos30^o = (√3)L.  This segment also serves as the normal line to the rays entering or exiting the prism at A or C'.  The length of the ray passing from A to A' can be found using the Pythagorean theorem,  ((L/2)² + 3L²)^½ = (√13)L/2.
  Snell's law:  sin30^o = n sinθ = n/(√13),  n = (√13)/2 = 1.803.

Lenses and mirrors

Problem:

A thin lens creates a sharp image of the object onto the wall.  The distance between the object and the wall is nine times the distance from the wall to the closest focal point. What is the object magnification?

Solution:

• Concepts:
  The thin lens
• Reasoning:
  We can use the lens equation, 1/x_o + 1/x_i = 1/f, and M = -x_i/x_o to solve the problem.
• Details of the calculation:
  Given:  A real image implies a converging lens, the image is inverted, f is positive, M is negative.
  
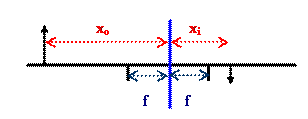
  x_i + x_o = 9(xi - f),  x_o = 8x_i - 9f.
  1/(8x_i - 9f) + 1/x_i = 1/f --> f² - 2x_if + (8/9)x_i² = 0,  f = x_i - (x_i² - (8/9)x_i²)^½,
  since f < x_i.
  f = (2/3)x_i,   x_i = (3/2)f,   x_o = 3f,   M = -x_i/x_o = -½.

Problem:

Suppose a certain object with a height of 1 cm is located 10 cm in front of its image, which has a height of 0.5 cm.  Both object and image are upright.  Find the location and focal length of a single thin lens that performs this imaging. 

Solution:

• Concepts:
  The thin lens equation
• Reasoning:
  This is a simple application of the thin lens equation.
• Details of the calculation:
  The image formed by the lens is upright.  It therefore is a virtual image.  The image is smaller than the object, it therefore is formed by a diverging lens.
  M = -x_i/x_o = 0.5,  x_i = -0.5 x_o, image and object are on the same side of the lens.
  x_o + x_i = 10 cm,  x_o - 0.5 x_o = 10 cm,  x_o = 20 cm
  1/x_o + 1/x_i = 1/f,  1/20 - 1/10 = 1/f,  f = -20 cm

Problem:

An object is placed 8 cm from a thin double convex lens of focal length 12 cm?
(a)  Find the image position and determine whether the image is real or virtual by using the lens formula.
(b)  Repeat part (a) by using graphical construction instead of the lens formula.

Solution:

• Concepts:
  The thin lens
• Reasoning:
  We are supposed to use the lens equation and a graphical construction to find the image position for a thin lens.
• Details of the calculation:
  (a)  Convex lens --> f is positive.
  1/x_o + 1/x_i = 1/f.  1/x_i = 1/12 - (1/8) = -1/24.  x_i = - 24, we have a virtual image.
  (b)  Graphical construction:

  

Problem:

A concave spherical mirror is used by a dentist to produce an enlarged image of a tooth.  If the radius of curvature of the mirror is 2.0 cm, how close is the mirror to the tooth when the image appears triple the size of the tooth?  Is the image erect or inverted?

Solution:

• Concepts:
  Spherical mirrors
• Reasoning:
  If an object is placed in front of a spherical mirror at an object distance x_o, then an image is formed at an image distance x_i, where x_o and x_i satisfy the mirror equation, 1/x_o + 1/x_i = 1/f.
  Sign conventions for the mirror equation:
  x_i is positive for a real image in front of the mirror surface, and x_i is negative for a virtual image behind the mirror surface.  x_o and x_i are the perpendicular distances from the center plane of the mirror as shown in the drawing on the right.
  The focal length f and the radius of curvature R = 2f are positive for a concave mirror and negative for a convex mirror.
  The magnification is M = h_i/h_o= -x_i/x_o.  If the magnification is negative, the image is inverted.
• Details of the calculation:
  The image is a virtual upright image.  f = 1 cm.  M = -3, x_i = -3x_o.  1/x_o  - (1/3)x_o = 2/(3x_o) = 1/(1 cm).
  x_o = (2/3) cm.

Problem:

Consider optical components centered on the x-axis.
A thin converging lens with focal length f = 2 cm is located at x = 0, and a convex mirror with radius of curvature |R| = 4 cm is located at x = d.
An object is placed at x = -3 cm.  Find the image location and magnification if
(a) d = 10 cm,
(b) d = 5 cm.
Is the image upright or inverted?

Solution:

• Concepts:
  Mirrors and lenses
• Reasoning:
  The image formed by the lens becomes the object for the mirror, the image formed by the mirror becomes the object for the lens after reflection.
• Details of the calculation:
  (a)  1.  Lens:  1/x_o + 1/x_i = 1/f, (1/3) + 1/x_i = ½, x_i = 6.  The image is located at x = 6 cm, 6 cm behind the lens and 4 cm in front of the mirror.
  The magnification is M₁ = -6/3 = -2.
  2.  Mirror:  f = -2,  ¼ + 1/x_i = -½, x_i = -4/3.  The image is located at x = 10 plus 4/3 cm, 4/3 cm behind the mirror, and 34/3 cm to the right of the lens.
  M₂ = (1/3).
  3.  3/34 + 1/x_i = ½.  x_i = 17/7.  The image is located at x = -17/7 cm.
  M₃ = -3/14.
  The magnification of the system is M₁*M₂*M₃ = 1/7.  The image is upright.
  (b)  1.  Lens:  1/x_o + 1/x_i = 1/f, (1/3) + 1/x_i = ½, x_i = 6.  The image is located at x = 6 cm, 6 cm behind the lens and 1 cm in behind the mirror.
  The magnification is M₁ = -6/3 = -2.
  2.  Mirror:  f = -2,  the object distance is negative.
  -1/1 + 1/x_i = -½, x_i = 2.  The image is located at x = 3 cm, 2 cm in front the mirror, and 3 cm to the right of the lens.
  M₂ = 2.
  3.  (1/3) + 1/x_i = ½.  x_i = 6.  The image is located at x = -6 cm.
  M₃ = -6/3 = -2.
  The magnification of the system is M₁*M₂*M₃ = 8.  The image is upright.

Problem:

An optical system comprises in turn, from left to right: an observer, a lens of focal length +30 cm, an erect object 20 mm high, and a convex mirror of radius 80 cm. The object is between the lens and the mirror, 20 cm from the lens and 50 cm from the mirror. The observer views the image that is formed first by reflection from the convex mirror and then by refraction from the lens. What is the position of this final image, measured from the mirror, and what is its height?

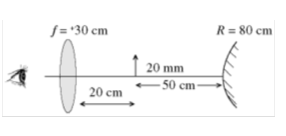
Solution:

• Concepts:
  Mirrors and lenses, 1/x_o + 1/x_i = 1/f
• Reasoning:
  The image formed by the mirror becomes the object for the lens after reflection.
• Details of the calculation:
  reflection:  f = -|R|/2 = - 40 cm.  1/50 + 1/x_i = -1/40,  x_i = -200/9 = 22.22. 
  The intermediate image is 200/9 cm to the right (behind) the mirror.
  M₁ = -x_i/x_o = 4/9 = 0.444.  The image is virtual and upright.
  refraction:  x_o = 830/9 cm.  9/830 +  1/x_i = 1/30,  x_i = 44.46. 
  The final image is 44.46 cm to the left (in front of) the lens.
  It is 114.46 cm to the left of the mirror.
  M₂ = -x_i/x_o = -44.46/92.22 = -0.482.  The image is real and inverted.
  M_final = M₁M₂ = -0.214.  The height of the final image is 4.3 mm and it is real and inverted.