Polarization

Problem:

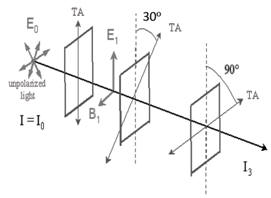
A unpolarized electromagnetic wave is incident on a series of three linear polarizers, the second with the polarization angle rotated at 30^o and the third at 90^o with respect to the first polarizer.  If the initial intensity of the unpolarized light is I₀, what is the intensity I₃ transmitted by the stack?

Solution:

• Concepts:
  Polarization
• Reasoning:
  For a polarized EM wave incident on a polarizer, I_transmitted = I₀ cos²θ.  Here θ the angle between E₀ and the transmission axis.
• Details of the calculation:
  After passing through the first polarizer, I₁ = I_o/2.
  After passing through the second polarizer I₂ = I₁ cos²(30^o).  
  Finally after passing through the third polarizer, I₃ = I₂ cos²(60^o).
  Thus, I₃ = I_o cos²(30^o)cos²(60^o)/2 = 0.094 I_o.

Problem:

(a)  Assume the electric field of a plane wave propagating in the z-direction oscillates in the x-direction.  What combination of polarizers would transmit the beam so it would emerge with the electric field oscillating in the y-direction.  Assume that perfect linear and circular polarizers are available.  Perfect linear polarizers transmit 100% of the incident wave in one plane of polarization and absorb 100% in the perpendicular plane.  Circular polarizers (quarter-wave plates) retard one plane of polarization ¼ wavelength relative to the perpendicular plane of polarization and hence can change a linearly polarized wave to a right- or left-hand circularly polarized wave and vice versa, depending on the orientation of the linear polarization.
(b)  What combination of polarizers would change a right-hand circularly polarized beam traveling in the z-direction into a left-hand circularly polarized beam.  How?

Solution:

• Concepts:
  Polarization, linear and circular polarizers
• Reasoning:
  We are supposed to find a combination of polarizers that rotate the polarization axis by 90^o.
• Details of the calculation:
  (a)  E = ε₀cos(kz - ωt)i describes the EM wave before polarizers are inserted in its path.
  Consider two coordinate systems rotated about the z-axis 45^o with respect to each other as shown below.
  
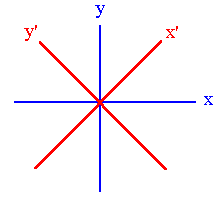
  Insert linear polarizer with its transmission axis along x' followed by a linear polarizer with its transmission axis along y.  After the first polarizer we have
  E = E₀cos(45^o)cos(kz - ωt + φ)i',
  and after the second polarizer we have
  E = E₀cos(45^o)²cos(kz - ωt + φ)j.
  The amplitude of the wave is reduced by a factor of 2 and the power by a factor of 4.
  To chance the linear polarization without reducing the amplitude we use two quarter-wave plates.  Assume the quarter-wave plate is oriented so the phase of light polarized along x' is retarded by π/2 with respect to the phase of light polarized along y'.
  Then we have before the plates
  E_x' = 2^-½E₀cos(kz - ωt),
  E_y' = -2^-½E₀cos(kz - ωt).
  After one quarter-wave plate we have
  E_x' = 2^-½E₀cos(kz - ωt + φ'),
  E_y' = -2^-½E₀cos(kz - ωt + φ' + π/2).
  After two quarter-wave plates we have
  E_x' = 2^-½E₀cos(kz - ωt + φ''),
  E_y' = -2^-½E₀cos(kz - ωt + φ'' + π) = 2^-½E₀cos(kz - ωt + φ'')
  E = E₀cos(kz - ωt + φ'')j.  The polarization has been rotated by 90^o but the amplitude has remained the same.
  (c)  Convention:  When viewed looking towards the source, a right circularly polarized beam at a fixed position as a function of time has a field vector that describes a clockwise circle, while left circularly polarized light has a field vector that describes a counter-clockwise circle
  RHC polarized light:  E_x' = E₀cos(kz - ωt), E_y' = E₀sin(kz - ωt)
  LHC polarized light:  E_x' = E₀cos(kz - ωt), E_y' = -E₀sin(kz- - ωt)
  After two quarter-wave plates the field of the RHC polarized wave becomes
  E_x' = E₀cos(kz - ωt+φ), E_y' = E₀sin(kz - ωt + φ + π) = -E₀sin(kz - ωt + φ).  The wave becomes a LHC polarized wave.

Problem:

(a)  Describe how to prepare a monochromatic plane wave of linearly polarized visible light.
(b)  Describe how to prepare a monochromatic plane wave of circularly polarized visible light

Solution:

• Concepts:
  Wavelength selection, polarization, linear and circular polarizers
• Reasoning:
  Prisms or gratings are dispersive elements.  Perfect linear polarizers transmit 100% of the incident wave in one plane of polarization and absorb 100% in the perpendicular plane.  Circular polarizers (quarter-wave plates) retard one plane of polarization ¼ wavelength relative to the perpendicular plane of polarization and hence can change a linearly polarized wave to a right- or left-hand circularly polarized wave and vice versa, depending on the orientation of the linear polarization.
• Details of the calculation:
  (a)  A plane wave in practical applications is a wave front with a well-defined direction of of propagation, extending over an area larger than the cross-sectional area of an object to be illuminated.
  The figure below shows a possible method of preparing a linearly polarized plane wave.
  
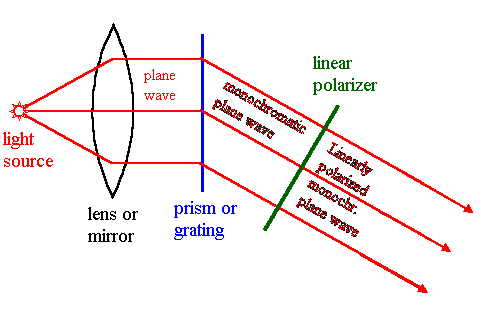
  (b)  The figure below shows a possible method of preparing a circularly polarized plane wave.