Wave optics
Diffraction and interference (slits)
Problem:
Consider a single slit diffraction pattern for a slit of
width d. Find the value of d if the angle between the first minimum and the
central maximum is 4*10-3 radians and the wavelength of the light is
633 nm.
Solution:
- Concepts:
Wave optics, the single slit diffraction pattern
- Reasoning:
Given the wavelength of the light we can find the slit width from the
diffraction pattern.
- Details of the calculation:
Single slit, first minimum: dsinθ = λ
d = (6.33*10-7 m)/(4*10-3) = 1.6*10-4 m
Problem:
A beam of monochromatic light with a wavelength of 500 nm
is directed through an absorber having 5 equally narrow slits separated by 20
μm between adjacent slits. The
resulting diffraction pattern is observed on a screen that is perpendicular to
the direction of light and 5 m from the slits. The intensity of the central
maximum is 1.3 W/m2.
(a) What are the distances from the central maximum to the first and second
principal maxima on the screen?
(b) What will be the intensity of the central maximum if there are only 4
equally narrow slits (of the same width as in part a), separated by 20
μm between adjacent slits?
Solution:
Problem:
Two gratings A and B have slit separations dA and dB,
respectively.
They are used with the same light source and the same observation screen. When
grating A is replaced with grating B, it is observed that the first-order
maximum of A is exactly replaced by the second-order maximum of B.
(a) Determine the ratio dB/dA.
(b) Find the next two principal maxima of grating A and the principal maxima of
grating B that exactly replace them when the gratings are switched. Identify
these maxima by their order numbers.
Solution:
- Concepts:
Interference
- Reasoning:
Constructive interference occurs when d sinθ = nλ.
- Details of the calculation:
a) dAsinθ = λ, dBsinθ = 2λ, dB/dA
= 2.
(b) 2nd-order maximum of A = 4th-order maximum
of B:
dAsinθ = 2λ, (dB/2)sinθ = 2λ, dBsinθ =
4λ.
3nd-order maximum of A = 6th-order maximum of B:
dAsinθ = 3λ, (dB/2)sinθ = 3λ, dBsinθ =
6λ.
Problem:
Light of wavelength 640 nm is
shone on a double-slit apparatus and the interference pattern is observed on a
screen. When one of the slits is covered with a very thin sheet of plastic of
index of refraction n = 1.6, the center point on the screen becomes dark. What
is the minimum thickness of the plastic?
Solution:
- Concepts:
Double slit interference
- Reasoning:
Destructive interference occurs when the optical path length difference is mλ/2,
with m = odd integer.
- Details of the calculation:
The geometrical path length from each slit to the center of the
diffraction pattern is the same. Let the thickness of the plastic
sheet be x. The optical path length through the plastic sheet is nx
and the optical path length difference is therefore (n - 1)x. We need
(n - 1)x = λ/2, for the minimum thickness n.
Alternatively:
Reaching the slits, the waves passing the slits are in phase. Upon
exiting the slits they have a phase difference (k' - k)x = (2πn/λ
- 2π/λ)x
=
(2π/λ)(n - 1)x.
For the minimum thickness we need (2π/λ)(n - 1)x
= π, x =
λ/(2(n-1)) =
λ/1.2 = 533 nm. The minimum
thickness is 533 nm.
Problem:
Suppose light from a Helium-Neon laser (wavelength
λ = 633 nm) is expanded and collimated into a beam with a
diameter of 2 cm, and then split into two beams that intersect as shown in the
drawing below. Let the polarization of the beam be perpendicular to the
plane of the drawing.
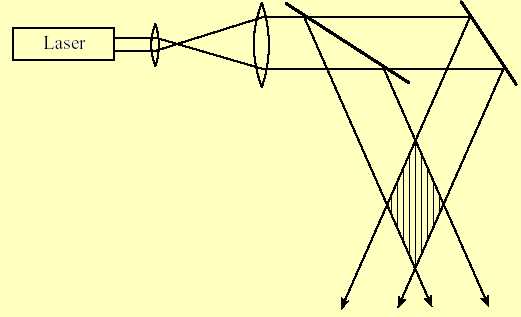
(a) If the full angle between the two overlapping beams is 10o,
how many fringes appear in the overlapping region?
(b) When the angle between the overlapping beams is increased to 30o, does the
fringe spacing in the overlap region increase or decrease? By how much?
Solution:
- Concepts:
Interference
- Reasoning:
In the regions where the beams overlap we have E =
E1
+ E2. The intensity is proportional to
<E(r,t)2>.
- Details of the calculation:
a) λ = 633 nm, beam diameter d = 2 cm. k1
= k2 = k = 2π/λ = 9.92*106 m-1.
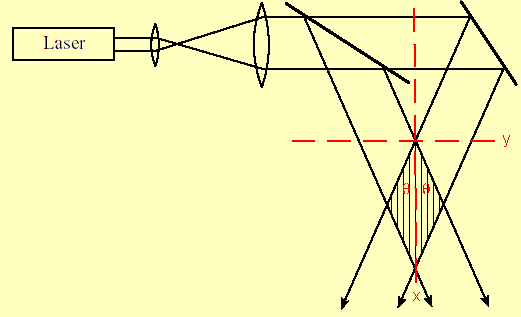
k1x = kcosθ, k2x = kcosθ, k1y = ksinθ, k2y
= -ksinθ.
In the regions where the beams overlap we have E =
E1
+ E2. Let E = Ek.
E(r,t) = A1cos(k1∙r-ωt) + A2cos(k2∙r-ωt).
E(r,t)2 = (A1cos(k1∙r-ωt))2
+ (A2cos(k2∙r-ωt))2 + 2A1cos(k1∙r-ωt)A2cos(k2∙r-ωt).
cosAcosB = ½[cos(A+B) + cos(A-B)]
cos(k1∙r-ωt+k2∙r-ωt) =
cos(2kcosθ x - 2ωt).
cos(k1∙r-ωt-k2∙r+ωt) =
cos(2ksinθ y)
E(r,t)2 = (A1cos(k1∙r-ωt))2
+ (A2cos(k2∙r-ωt))2 + A1A2[cos(2kcosθ
x - 2ωt)+cos(2k1sinθ y)]
<I>
 <E(r,t)2>
<E(r,t)2>
The average values of cos2(k1∙r-ωt) and cos2(k2∙r-ωt)
are ½, and cos(2kcosθ x - 2ωt) is zero, when averaged over a large number of
periods.
<E(r,t)2> = A12/2 +A22/2
+ A1A2cos(2ksinθ y)]
<I> = <I1> + <I2> + 2(<I1><I2>)½cos(2ksinθ
y)]
The intensity therefore varies with y as C1 + C2cos((2π/λ')y)
= C1 + C2cos(2ksinθ y).
λ' = π/ksinθ.
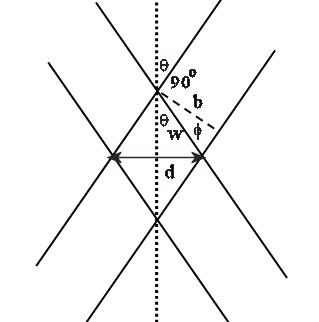
How many λ' fit into d, the maximum width of the overlapping region?
Φ = 90o - 2θ, w = b/cosΦ = b/sin(2θ), d/2 = wsinθ, d =
2bsinθ/sin(2θ)
The maximum width of the overlap region is 4 cm*sinθ/sin(2θ) = 2 cm/cos(θ).
The maximum number of fringes is (2 cm/cos(θ))/(π/ksinθ) = 4*tan(θ)/6.33*10-5.
When θ = 5o, then λ' = 3.63*10-6
m, we observe 5529 fringes.
(b) When θ = 15o, then λ' = 1.22 10-6
m, we observe 16932 fringes
Problem:
Two radio-frequency sources, A
and B, a distance 4 m apart, are radiating in phase radiation of wave length
λ = 1 m. You move a detector on the
circular path of radius R >> 4 m around the two sources in a plane containing
them. How many maxima do you detect?
Solution:
- Concepts:
Interference, two sources
- Reasoning:
We expect a "double slit" interference pattern.
- Details of the calculation:
The condition for constructive interference for two sources which oscillate
in phase is
dsinθ = mλ,
sinθ = mλ/d
. Here sinθ = m/4.
For 0 ≤ θ < 2π
we can satisfy this condition 16 times.
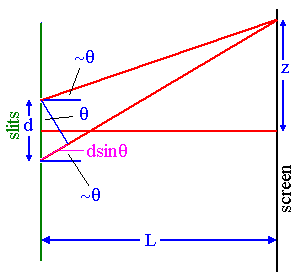
Problem:
A monochromatic wave of wavelength λ illuminates an opaque mask with two slits as shown in the
figure. The diffraction pattern is recorded on a screen a distance L from the
mask. You may assume that λ << d. D << L.
(a) What is the distance Λ between
adjacent interference fringes observed on the screen?
(b) What is the width Δx of the central
lobe of the interference pattern on the screen?

Solution:
- Concepts:
Wave optics, the single and the double slit interference pattern
- Reasoning:
The distance Λ between adjacent
interference fringes is the distance between adjacent maxima of the double
slit interference pattern.
The width Δx of the central lobe of
the interference pattern equals twice the distance from the central maximum
to the first minimum of the single slit interference pattern.
- Details of the calculation:
(a) For the distance between adjacent maxima of the double slit pattern we
have Dsinθ = λ.
Here sinθ ≈
θ ≈ Λ/L. So Λ = λL/D.
(b) For the distance from the central maximum to the first minimum of
the single slit interference pattern we have dsinθ = λ.
Here sinθ ≈ θ ≈
Δx /(2L). So Δx = λ2L/d.
Thin film interference
Problem:
A thin film of antireflection coating having refractive index of 1.35 and
thickness 452 nm covers surface of a glass plate (nglass = 1.55). The
coating is designed so that there is minimal reflectance at normal incidence for
488 nm light. What is the smallest angle of incidence for which this coating
produces constructive interference for a reflected 488 nm light beam?
Solution:
- Concepts:
Thin film interference
- Reasoning:
When a light wave reflects from a medium with a larger index of refraction,
then the phase shift of the reflected wave with respect to the incident wave is
π or 180o.
When a light wave reflects from a medium with a smaller index
of refraction, then the phase shift of the reflected wave with respect
to the incident wave is zero.
- Details of the calculation:
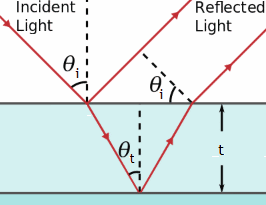
Waves incident at an angle θi on the air coating interface are refracted
as they enter the coating. The angle
of refraction θt is found from
Snell's law, nairsinθi = ncsinθt. If
the waves are reflected off the second interface, then they travel a
distance 2t/cosθt in the coating.
When they emerge again from the coating into the air and propagate parallel
to the waves reflected at the air-coating interface, then the total optical
path length difference is
2 nc t/cosθt - 2t tanθtsinθi
= 2 nc t/cosθt - 2t tanθt(nc/nair)sinθt
= (2nct/cosθt)(1 - sin2θt)
= 2 nc t cosθt = 2 nc t(1 - (nair/nc)2sin2θi)½.
[The optical path length (OPL) of a
light ray traveling from point A to point B is defined as c times
the time it takes the ray to travel from A to B. In free space
the optical path length is just the distance d between the points.
In a transparent medium with index of refraction n, it equals n
times this distance, OPL = nd, because the light moves with speed c/n.]
We get a phase shift of π for the waves reflected from both interfaces.
For constructive interference we therefore need 2 nc t cosθt
= mλ, m = 1, 2,... .
Using the given t, λ, and nc we find cosθt
= m*0.4.
For the smallest θt, we need m = 2, cosθt
= 0.8, sinθt
= 0.6,
sinθi
= 0.81, θi
= 54o.
Circular apertures, resolution
Problem:
A spy satellite travels at a distance of 50 km above Earth's surface. How
large must the lens be so that it can resolve objects with a size of 2 mm and
thus read a newspaper? Assume the light has a wavelength of 400 nm.
Solution:
- Concepts:
Diffraction and resolution
- Reasoning:
Diffraction limits the resolution according to θ = 1.22 λ/D = y/L.
- Details of the calculation:
Here the height of the object to be resolved is y and the distance to the
object is L. Solving for D we find D = 12.2 m.
Problem:
For an ideal telescope, the limiting resolution is the size of the Airy
disk. However, turbulence in Earth's atmosphere produces pockets of denser air
which refract light rays from distant stars, causing them to strike a telescope
detector at slightly different locations. At sea level, this imposes an
effective resolution limit of 1 arc-second (1/3600 degree) regardless of the
size of the telescope. For what diameter of telescope does this represent the
diffraction limit for blue light (λ = 400 nanometers)?
Solution:
- Concepts:
Diffraction and resolution
- Reasoning:
Diffraction limited resolving power: θmin = 1.22 λ/D
- Details of the calculation:
D = 1.22 λ/θmin. Here θmin = 4.85*10-6 rad,
so the diameter of the telescope
D = (1.22*4*10-7/4.85*10-6) m = 10 cm.
Bragg reflection
Problem:
(a) An incident monochromatic x-ray beam with wavelength
λ = 1.9 Å is
reflected from the (111) plane in a 3D solid with a Bragg angle of 32o
for the n = 1 reflection. Compute the distance (in
Å) between adjacent (111) planes.
(b)
Assuming that the solid has a fcc lattice, use the result from part (a) to
compute the lattice constant a (in Å).
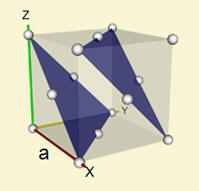
(111) planes, FCC lattice
Solution:
- Concepts:
Bragg reflection
- Reasoning:
In Bragg reflection the condition for constructive interference is: nλ =
2d sinθ, where θ is the angle between the incident wave vector and the
scattering planes.
- Details of the calculation:
(a) d = λ/(2 sinθ) = 1.9 Å /(2*sin32o)
= 1.79 Å is the distance between adjacent
(111) planes.
(b) From geometry: 3d = (3a2)½, a = d*√3 = 3.1
Å is the lattice constant.


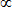 <E(r,t)2>
<E(r,t)2>



