Perfect conductor boundaries, Waveguides

Problem:

(a)  Beginning with the free Maxwell equations in unbounded space, show that the propagation of an electromagnetic wave is transverse.  That is, show that the electric and magnetic fields oscillate in a plane perpendicular to the direction of propagation and perpendicular to each other.
(b)  Now, consider the reflection of a plane electromagnetic wave from a flat perfect conductor.  Note that a perfect conductor develops a charge and current distribution on the surface so that external fields do not penetrate it.  Find the charge and current densities on the conductor for the case of polarization in the plane of incidence.

Solution:

• Concepts:
  Maxwell's equations, boundary conditions
• Reasoning:
  Maxwell's equations in free space  yield the wave equation for both E and B.  They can also be used to show that E ⊥ B.  E ⊥ k.  B ⊥ k.  B = (μ₀ε₀)^½(k/k)×E.
• Details of the calculation:
  (a)  Maxwell's equations:
  ∇∙E = ρ/ε₀,  ∇×E = -∂B/∂t,  ∇∙B = 0,  ∇×B = μ₀j + (1/c²)∂E/∂t.
  Assume ρ_f and j_f are zero in the medium.  Then
  ∇×(∇×E) = ∇(∇∙E) - ∇²E = -(∂/∂t)(∇×B) = -μ₀ε₀∂²E/∂t².
  ∇²E = μ₀ε₀∂²E/∂t².
  ∇×(∇×B) = ∇(∇∙B) - ∇²B = μ₀ε₀(∂/∂t)(∇×E) = -μ₀ε₀∂²B/∂t².
  ∇²B = μ₀ε₀∂²B/∂t².
  Each Cartesian component of E and B satisfies the 3-dimensional, homogeneous wave equation.
  Plane wave solutions E = E((k/k)∙r - ct).  B = B((k/k)∙r - ct) exist.  (k/k denotes the direction of propagation.)
  Let u = (k/k)∙r - ct.
  ∇∙E = ∂E_x/∂x + ∂E_y/∂y +∂E_z/∂z
  = (∂E_x/∂u)(k_x/k) + (∂E_y/∂u)(k_y/k) +(∂E_z/∂u)(k_z/k) = (∂/∂u)(E∙(k/k)) = 0.
  E∙k = constant = 0 if we are not interested in static fields.
  ∇∙E = 0 requires that E∙k = 0 for radiation fields, i.e. that E is perpendicular to k.
  Similarly, ∇∙B = 0 requires that B∙k = 0 for radiation fields.
  ∇×E = -∂B/∂t requires that ((k/k)×E = cB.  i.e.  B is perpendicular to E and k.
  [(∇×E)_x = ∂E_z/∂y - ∂E_y/∂z = (∂E_u/∂u)(k_y/k) - (∂E_y/∂u)(k_z/k)
  = (∂/∂u)((k/k)×E)_x = -∂B_x/∂t = (∂B_x/∂u)c.
  If we are not interested in static fields then ((k/k)×E)_x = cB_x.
  Repeating this derivation for the y- and z- components we have ((k/k)×E = cB.]
  
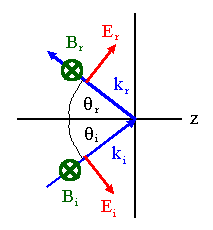
  (b)  The tangential component of E is continuous at z = 0.  This implies E_icos(θ) = E_rcos(θ) at z = 0, E_i = E_r.
  The normal component of E then is E_isin(θ) + E_rsin(θ) = 2E_isin(θ).
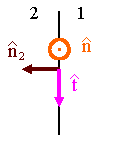
  The surface charge density is σ = ε₀2E_isin(θ).  [(E₂ - E₁)∙n₂ = σ/ε₀ ]
  The tangential component of B at the z < 0 side of the surface is B_r + B_i = 2B_i.
  Therefore 2B_i/μ₀ = k.  (Here k = surface current density.)  [(B₂ - B₁)∙t = μ₀k∙n]
  

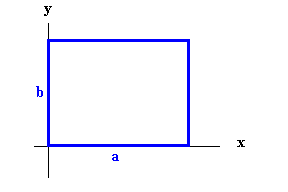
Problem:

Consider a rectangular conducting waveguide of width a (along the x axis) and height b (along the y axis).  An EM wave of wavelength λ travels into the guide along the z axis; the amplitude of the wave has the form E_y = E₀sink_xx.  Derive the form of the guided wavelength and discuss the meaning of the critical (cutoff) wavelength.

Solution:

• Concepts:
  Waveguides, boundary conditions
• Reasoning:
  In a rectangular channel with its axis in the z-direction TE_0n waves of the form E = E₀sink_xx exp(i(k_zz-ωt)) j can propagate.  They have to satisfy the wave equation and the boundary conditions E∙t = 0 and B∙n = 0 on the walls of the channel.  These conditions can only be satisfied if ω < ω_c, where  ω_c is called the cutoff frequency.
• Details of the calculation:
  
  A wave traveling into the z-direction that satisfies the boundary conditions E∙t = 0 on the walls if we have E = E₀sink_xx exp(i(k_zz-ωt)) j.  k_xa = nπ.  The wave equation requires 
  ∇²E_y = (1/c²)∂²E_y/∂t² or k_x²E_y + k_z²E_y - (ω²/c²)E_y = 0.
  k_x² + k_z² = (ω²/c²).  Since we know k_x we can solve for k_z.
  k_z = ((ω²/c²) - (nπ/a)²)^½.
  Check if B satisfies the boundary conditions B∙n = 0 at the walls:
  ∇×E = -(∂E_y/∂x)(z/z) + (∂E_y/∂z)(x/x) = iωB.
  B = [(k_z/ω)E₀sink_xx(x/x) + (ik_x/ω))E₀cosk_xx(z/z)] exp(i(k_zz-ωt)).
  B∙n = 0 on the walls.
  The wave satisfies the wave equation and the boundary conditions.
  The electric field is transverse to the channel, we have a TE wave.  The mode is TE_0n.
  k_z becomes imaginary and the wave does not propagate if 
  (ω²/c²) < (nπ/a)² or ω < nπc/a.
  λ = 2πc/ω.  If λ > λ_c = 2a/n then the TE_0n mode cannot propagate.
  If a > b then λ_c = 2a is the cutoff wavelength for all TE modes.

Problem:

A rectangular waveguide of sides a = 7.21cm and b = 3.40cm is used in the transverse magnetic (TM) mode.  Assume that the walls are perfect conductors.
(a)  By calculating the lowest cut off frequency, determine whether TM radiation of angular frequency ω = 6.1*10¹⁰ s^-1 will propagate in the waveguide.
(b)  What is the dispersion relation for this guide?
(c)  Find the attenuation length for a frequency ω that is half the cut off frequency.

Solution:

• Concepts:
  Waveguides, boundary conditions
• Reasoning:
  
  A TM wave is a superposition of waves of the form 
  B = B_0xsink_xx exp(i(k_zz-ωt)) i + B_0ysink_yy exp(i(k_zz-ωt)) j,
  with  k_xa = nπ,  k_yb = mπ, with m and n nonzero, positive integers. 
  These waves is called the TM_nm modes of the waveguide.
  TM₁₀ or TM₀₁ guided waves do not exist.
• Details of the calculation:
  (a)  B_x = B_0xsink_xx exp(i(k_zz-ωt)),  B_y = B_0ysink_yy exp(i(k_zz-ωt).
  B∙n = 0 on the walls requires
  k_xa = nπ,  k_yb = mπ, with m and n nonzero, positive integers.
  We need ∇∙B = 0, ∂B_x/∂x + ∂B_y/∂y = 0.
  This yields k_xB_0xcosk_xx + k_yB_0ycosk_yy = 0,
  B_0x = -B_0y(k_ysink_yy)/(k_xcosk_xx).
  If we choose B_0y = k_xB₀cosk_xx and B_0x = -k_yB₀cosk_yy
  then the equation is satisfied.
  We have B = (-k_ycosk_yy sink_xx i + k_xcosk_xx sink_yy j)B₀exp(i(k_zz-ωt))
  The wave equation requires  ∇²B - (1/c²)∂²B/∂t² = 0.
  k_x²B + k_y²B + k_z²B - (ω²/c²)B = 0.
  k_x² + k_y² + k_z² = (ω²/c²).  Since we know k_x and k_y we can solve for k_z.
  k_z = ((ω²/c²) - (nπ/a)² - (mπ/b)²)^½.
  The cutoff frequency for the TM_nm mode is ω_c = c((nπ/a)² + (mπ/b)²)^½.
  The cutoff frequency for the TM₁₁ mode is ω_c = c((π/a)² + (π/b)²)^½ = 3.1*10^-10 s^-1, so TM radiation of angular frequency ω = 6.1*10¹⁰ s^-1 will propagate in the waveguide.
• (b)  The dispersion relation gives ω as a function of k_z.
  ω = c(k_z² + (nπ/a)² +(mπ/b)²)^½.
  (c)  k_z = (1/c)(ω² - ω_c²)^½.  If ω = ω_c/2 then k_z = (i/c)(√3)ω_c/2.
  We have:  B proportional to exp(-k_zz) = exp(-(√3)ω_cz/(2c)).
  Therefore:  Power P proportional to B² proportional to exp(-(√3)ω_cz/c).
  We want:  P(z)/P(0) = 1/e,  z = c/(√3)ω_c = 3*10⁸ m/(3.1*10^-10*√3) = 5.6*10^-3 m.

Problem:

A rectangular waveguide made of perfectly conducting material has sides of length a and b as shown in the figure below.

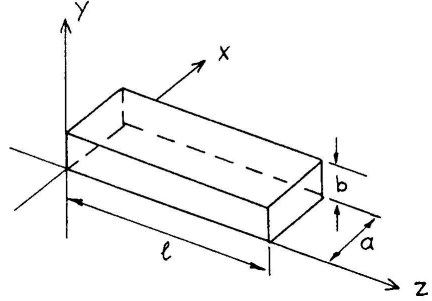
The ends of a section of length l are covered with plates of conducting material, i.e. the waveguide is effectively a resonant cavity.  If the electric field is given by the real part of

E(x,y,z,t) = E₀(x,z)e^iωt j,

what is ω for the cavity mode with the lowest resonant frequency?

Solution:

• Concepts:
  Maxwell's equations, waveguides, resonant cavities
• Reasoning:
  The electric field in the cavity must satisfy Maxwell's equations and the boundary conditions E∙t = 0 and B∙n = 0 on the walls of the cavity. 
• Details of the calculation:
  Given: E(x,y,z,t) = E₀(x,z)e^iωt (y/y),  B proportional to e^iωt.
  The field has to satisfy Maxwell's equations.  Does it?
  ∇∙E = 0, ∂E_y/∂y = 0.  This equation is satisfied.
  ∇×E = -(∂E_y/∂z)(x/x) + (∂E_y/∂x)(z/z) = -∂B/∂t = -iωB.
  This implies that B = (1/(iω))(∂E_y/∂z)(x/x) - (1/(iω))(∂E_y/∂x)(z/z).
  ∇∙B = (1/(iω))[∂²E_y/∂x∂z - ∂²E_y/∂z∂x] = 0.  This equation is satisfied.
  B = B_x(x,z)(x/x) + B_z(x,z)(z/z).
  ∇×B = [∂B_x/∂z) - (∂B_z/∂x)](y/y) = (1/c²)∂E/∂t = (iω/c²)E₀(x,z)e^iωt (y/y).
  The given field satisfies Maxwell's equations.
  If we choose E₀(x,z) = Asin(k_xx)sin(k_zz) with k_xa = nπ, k_zl = mπ, then E∙t = 0 is satisfied on all walls.
  With this choice B_x = (1/(iω))k_zAsin(k_xx)sin(k_zz), B_x = 0 at x = 0 and x = a.
  B_z = (-1/(iω))k_xAsin(k_xx)sin(k_zz), B_z = 0 at z = 0 and z = l.
  B∙n = 0 is satisfied on all walls.
  [∂B_x/∂z) - (∂B_z/∂x)] = (iω/c²)E₀(x,z)e^iωt requires -(1/(iω))k_z² - (1/(iω))k_x² = (iω/c²).
  -k_z² - k_x² + ω²/c² = 0.  ω²/c² = (mπ/l)² + (nπ/a)².
  The lowest resonance frequency in the cavity is ω = c*[(π/l)² + (π/a)²]^½.