Point charge in non-periodic motion

Problem:

A charged particle A, moving with v << c, decelerates uniformly.  A second particle B has one-half the mass, twice the charge, three times the velocity, and four times the acceleration of particle A.  Find the ratio P_B/P_A of the powers radiated.

Solution:

• Concepts:
  The Larmor formula
• Reasoning:
  The Larmor formula is an expression for the total power radiated by a a point charge moving non-relativistically.
• Details of the calculation:
  Larmor formula: :  P = -dE/dt = [q²/(6πε₀c³)]a². 
  P_B/P_A = q_B²a_B²/(q_A²a_A²) = 4*16 = 64.

Problem:

Electrons in a computer monitor CRT are accelerated to a final kinetic energy of 30 keV over a distance of 1 cm, then are rapidly decelerated to zero speed in collisions with the screen phosphor.  Assume both acceleration and deceleration are constant.  Consider the energy radiated by accelerated electrons (which has nothing directly to do with the light emitted by the phosphor).
(a)  Can this problem be treated non-relativistically?  Explain why or why not.
(b)  Develop an expression for the ratio r of the energy radiated during the acceleration phase, E_rad, to the final kinetic energy E_kin, assuming constant acceleration a.  Also calculate a numeric value for r under the conditions pertaining to the acceleration of electrons in the monitor CRT described above.
(c)  Again assuming constant acceleration, estimate the maximum total fraction of kinetic energy that is radiated during the stopping of the electrons in the phosphor, and from that, the average power radiated per stopped electron in watts.  Assume all the kinetic energy is consumed in single collisions in a distance of 0.05 nm within single atoms of the phosphor.

Solution:

• Concepts:
  Radiation produced by accelerating charges, the Larmor formula
• Reasoning:
  We are asked to determine the energy radiated by an accelerating electron.
• Details of the calculation:
  (a)  The rest energy of the electron is 510 keV, its maximum kinetic energy is 30 keV.
  γ_max510 = 540,  γ_max = 1.06 ≈ 1.  The problem can be treated nonrelativistically.
  (b)  An accelerating charged particle radiates away energy.  If for a time T the magnitude of the acceleration is a, then the energy radiated E_rad = 2e²a²T/(3c³) is given by the Larmor formula.  If the particle is initially at rest, and we neglect radiation, then the kinetic energy of the particle after time T will be E_kin = ½ma²T².
  E_rad << E_kin, if 2e²a²T/(3c³) << ½ma²T²,  T >> (4/3)e²/(mc³) = (4/3)r₀/c.
  For an electron r₀ ≈ 3*10^-15m.
  If T is much greater than the time it takes light to travel 4*10^-15m ( or if T >> 10^-23 s) then we can neglect radiation losses when considering the short term motion.
  E_rad/E_kin = 4e²/(3c³mT).
  ½ma²T² = 30000*1.6*10^-19J.  a = (30000V/0.01m)(1.6*10^-19C/9.1*10^-31kg).
  T = 1.94*10^-10s.  E_rad/E_kin = 6.4*10^-14.
  (c)  E_kin = ½ma²t² = 30 keV.  From kinematics:  d = ½at².  Therefore a = E_kin/md.
  t² = 2d²m/E_kin = 2(5*10^-11m)²(9.1*10^-31kg)/(3*10⁴*1.6*10^-19J).  t = 9.7*10^-19s.
  E_rad/E_kin = 1.3*10^-5.  <P> = E_rad/t = 0.06W.

Problem:

An electron is released from rest and falls under the influence of gravity.  In the first centimeter, what fraction of the potential energy lost is radiated away?

Solution:>

• Concepts:
  The radiation field of a point charge moving non-relativistically, the Larmor formula
• Reasoning:
  We are asked to determine the energy radiated by an accelerating electron.
• Details of the calculation:
  The rest energy of the electron is 510 keV, the change in gravitational potential energy is
  mgΔh = 9.1*10^-31*9.8*10^-2J = 5.6*10^-13 eV. 
  This problem can be treated non-relativistically.
  An accelerating charged particle radiates away energy.
  If for a time T the magnitude of the acceleration is a, then the energy radiated
  E_rad = 2e²a²T/(3c³) is given by the Larmor formula. 
  If the particle is initially at rest, and we neglect radiation,
  then the kinetic energy of the particle after time T will be E_kin = ½ma²T².
  E_rad/E_kin = 4e²/(3c³mT).
  We find T from kinematics:  d = ½gt².  Here t = 4.52*10^-2 s.
  E_rad/E_kin = 2.7 10^-22.
  Since the fraction of the energy radiated away is so small, E_kin is equal to the potential energy lost.

Problem:

In a large region of space the electric field is constant and homogeneous, E = Ei, and gravity can be neglected.  A point mass m with charge q moves through the origin at
t_i = 0 with velocity v = (v₀cosα, 0, v₀sinα), with v₀ << c and cosα > 0.
At some later time t_f  the x coordinate of the particle is L and the particle is still moving with v_f  << c.
(a)  Find the z-coordinate of the particle at t = t_f.
(b   Find the total energy radiate between t_i and t_f as a function of the variables given.

Solution:

• Concepts:
  Kinematics, the Larmor formula
• Reasoning:
  We have motion with constant acceleration acceleration a = (qE/m)i.
• Details of the calculation:
  (a)  Neglecting radiation, the equation of  motion is F = qE.
  a_x = qE/m, a_y = a_z = 0.  L = v₀cosα t_f + ½(qE/m)t_f²,  z(t_f) = v₀sinα t_f.
  We can solve for t_f in terms of L.
  t_f = [-mv₀cosα + (m²v₀²cos²α + 2qEmL)^½]/(qE)
  z(t_f) = v₀sinα [-mv₀cosα + (m²v₀²cos²α + 2qEmL)^½]/(qE).
  (b)  The power is given by the Larmor formula. P = q²a²/(6πε₀c³)
  The energy radiated is
  E = Pt_f = μ₀q³Ev₀[-cosα + (cos²α + 2qEL/(mv₀²))^½]/(6πmc).

Problem:

A ball with a total charge of 1 Coulomb and a mass 1 kg is dropped from the top of a tall building of height 100 m. What is the total power radiated as a function of height? (Ignore air friction).

Solution:

• Concepts:
  The radiation field of a point charge moving non-relativistically, the Larmor formula
• Reasoning:
  We are asked to determine the energy radiated per unit time by an accelerating charge.
• Details of the calculation:
  This problem can be treated non-relativistically.
  An accelerating charged particle radiates away energy.
  Power radiated = q²a²/(6πε₀c³).  Here a² = g².
  P = (1 C)²(9.8 m/s²)²/(6πε₀c³) = 2.13*10^-14 J/s.
  The power radiated is independent of the height.
  The total energy radiated as a function of distance s fallen is E_rad = Pt = P(2s/g)^½.
  For s = 100 m we have E_rad = 9.6*10^-14 J, completely negligible compared to the potential energy lost or kinetic energy gained.

Problem:

A linear accelerator of length 10 m uniformly accelerates protons to kinetic energy 100 MeV.  Ignore relativistic effects.
(a) What is the power radiated by each proton (Watts)?
(b) What fraction of the energy imparted to the protons is lost to radiation?
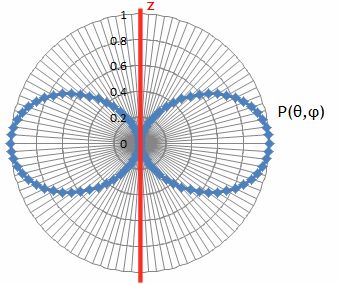
(c) Sketch the normalized (1 = max) power pattern of the radiation [use a polar plot, indicate the direction of motion of the protons].

Solution:

• Concepts:
  The radiation field of a point charge moving non-relativistically, the Larmor formula
• Reasoning:
  We are asked to determine the power radiated by an accelerating proton.
• Details of the calculation:
  (a)  An accelerating charged particle radiates away energy.
  Power radiated = q²a²/(6πε₀c³).
  Here a = v²/(2Δx) = E/(mΔx) (kinematics).
  a = (1.6*10^-11 J)/(1.672*10^-27 kg * 10 m) = 9.57*10¹⁴ m/s².
  P = (1.6*10^-19 C)²( 9.57*10¹⁴ m/s²)²/(6πε₀c³) =  5.2*10^-24 J/s.
  (b)  If for a time T the magnitude of the acceleration is a, then the energy radiated is
  E_rad = q²a²T/(6πε₀c³).
  If the particle is initially at rest, and we neglect radiation,
  then the kinetic energy of the particle after time T will be E_kin = ½ma²T².
  E_rad/E_kin = q²/(3πε₀c³mT).
  We find T from kinematics:  d = ½aT².  Here T = 1.45*10^-7 s.
  E_rad/E_kin = 4.7*10^-20.
  (c) If the direction of motion is the z-direction, the direction of the acceleration is the z-direction.
  P(θ,φ)dΩ is proportional to (a_⊥)², therefore P(θ,φ) is proportional to sin²θ, where θ is the usual polar angle.  P(θ,φ) has no φ dependence.