Antennas

Problem:

Consider a linear antenna of length d (d << λ) with a narrow gap in the center for the purposes of excitation.  Assume that the current is sinusoidal and in the same direction in each half of the antenna, having a value of I₀ at the gap and falling linearly to zero at the ends.  Find the power radiated in the electric dipole approximation.

Solution:

• Concepts:
  Radiation from antennas, dipole radiation
• Reasoning:
  We can treat the antenna as made up of small sections, each section emitting dipole radiation.
• Details of the calculation:
  Consider a small section of the antenna of length dz' located at z' .  Treat it like a dipole.
  Let p(z') = q(z')dz'(z/z), q(z') = q₀(z')cosωt.
  Then I(z') = dq(z')/dt = -ωq₀(z')sinωt = I₀(z')sin(ωt),  I₀(z') = -ωq₀(z').
  p(z') = p₀(z')cosωt.  p₀(z') = q₀(z')dz = -(I₀(z')/ω)dz.
  For dipole at the origin we have E_R(r,t) = -(1/(4πε₀c²r))ω²p₀ cos(ω(t - r/c))sinθ (θ/θ).
  A small section of the antenna of length dz' located at z' a distance R = r - (z/z)z' from the observation point therefore produces
  dE_R(r,t) = (1/(4πε₀c²R))ω²(I₀(z')/ω)cos(ω(t - R/c))sinθ'dz' (θ'/θ').
  dB_R(r,t) = (1/(4πε₀c³R))ω²(I₀(z')/ω)cos(ω(t - R/c))sinθ'dz'(φ/φ).
  Assume r >> λ, r >> z', d << λ.
  Then θ' ≈ θ = constant, for all sections of the antenna.
  We can also replace 1/R by 1/r and cos(ωt - kR) by cos(ωt - kr) because the changes in kR are small compared to π/2 over the length of the antenna.  (k = ω/c)
  I₀(z) = I₀ - (2I₀/d)|z|, the current falls linearly to zero at the ends.
  E_θ(r,t) = ∫_z=-d/2^z=d/2dE_θ(r,t) = 2 ∫₀^z=d/2dE_θ(r,t)
  = (I₀ω/(2πε₀c²r))cos(ω(t - r/c))sinθ ∫₀^z=d/2(1 - 2z/d)dz'
  = (I₀d ω²/(8πε₀c³))(1/(kr))cos(ω(t - r/c))sinθ.
  B_φ(r,t) = ∫_z=-d/2^z=d/2dB_φ(r,t) = 2 ∫₀^z=d/2dB_φ(r,t)
  = (μ₀I₀d ω²/(8πc²))(1/(kr))cos(ω(t - r/c))sinθ.
  S = (1/μ₀)E×B = (r/r)[(I₀²d²ω⁴/(64π²ε₀c⁵k²r²))cos²(ω(t - r/c))sin²θ.]
  P = (I₀²d²ω²/(64π²ε₀c³r²))cos²(ω(t - r/c)) ∫2πr² sin³θ dθ
  = (I₀²d²ω²/(32πε₀c³))cos²(ω(t - r/c))(4/3).
  <P> = ½(I₀²d²ω²/(24πε₀c³)) is the average power radiated in the electric dipole approximation.

Problem:

Assume an antenna is aligned with the z-axis and extends from z = -λ/4 to z = +λ/4.  Assume the current in the antenna varies as I(z,t) = I₀sin(ωt)cos(kz).  Calculate the radiation fields E_R and B_R and the average Poynting vector.

Solution:

• Concepts:
  Radiation from antennas, dipole radiation
• Reasoning:
  We can treat the antenna as made up of small sections, each section emitting dipole radiation.
• Details of the calculation:
  Consider a small section of the antenna.  Treat it like a dipole.
  Let p(z) = q(z) dz (z/z), q(z) = q₀(z)cosωt.
  Then I(z) = dq(z)/dt = -ωq₀(z)sinωt = I₀(z)sin(ωt),  I₀(z) = -ωq₀(z).
  p(z) = p₀(z)cosωt.  p₀(z) = q₀(z)dz = -(I₀(z)/ω)dz.
  Here I₀(z) = I₀cos(kz)
  For dipole at the origin we have E_R(r,t) = -(1/(4πε₀c²r))ω²p₀(0) cos(ω(t - r/c))sinθ (θ/θ).
  A small section of the antenna of length dz' located at z' a distance R = r - (z/z)z' from the observation point therefore produces
  dE_R(r,t) = (1/(4πε₀c²R))ω²(I₀/ω)cos(ω(t - R/c))sinθ'cos(kz')dz' (θ/θ).
  dB_R(r,t) = (1/(4πε₀c³R))ω²(I₀/ω)cos(ω(t - R/c))sinθ'cos(kz')dz'(φ/φ).
  
  dE_θ(r,t) = (ω²I₀/(4πε₀c³))[cos(ω(t - R/c))/kR]sinθ'cos(kz')dz',
  dB_φ(r,t) = (ω²I₀/(4πε₀c⁴))[cos(ω(t - R/c)/kR]sinθ'cos(kz')dz',
  with k = ω/c.
  E_θ(r,t) = (ω²I₀/(4πε₀c³))∫[cos(ω(t - R/c))/kR]sinθ'cos(kz')dz',
  B_φ(r,t) = (ω²I₀/(4πε₀c⁴))∫[cos(ω(t - R/c)/kR]sinθ'cos(kz')dz'.
  The integration limits are -λ/4 and λ/4.
  Assume r >> λ, r >> z'.
  Then θ' ≈ θ = constant for all sections of the antenna.
  But cos(ωt - kR) ≠ cos(ωt - kr) because kR changes by π/2 over the length of the antenna.  Although kR >> π/2, this changes the phase drastically.
  We use kR = kr - kz'cosθ for the argument of the cosine function.  We, however, can safely replace 1/R by 1/r.
  
  We then have
  E_θ(r,t) = (ω²I₀sinθ/(4πε₀c³kr))∫cos(ωt - kr + kz'cosθ)cos(kz')dz',
  B_f(r,t) = (μ₀ω²I₀sinθ/(4πc²kr))∫cos(ωt - kr + kz'cosθ)cos(kz')dz'.
  ∫_-λ/4^λ/4cos(ωt - kr + kz'cosθ)cos(kz')dz'
  = (1/k)cos(ωt - kr)∫_-π/2^π/2cos(kz'cosθ)cos(kz')dkz'
  - (1/k)sin(ωt - kr)∫_-π/2^π/2sin(kz'cosθ)cos(kz')dkz'.
  The second integral is zero, since it is an integral over an odd function of z'.
  
  ∫_-π/2^π/2cos(ax) cos(x)dx = sin((a-1)x)/(2(a-1)) + sin((a+1))x/(2(a+1))|_-π/2^π/2
  = [1/(2(a-1))]{sinaxcosx-sinxcosax} + [1/(2(a+1))]{sinaxcosx+sinxcosax}|_-π/2^π/2
  = [1/(2(a-1))]{-2cos(a(π/2))} + [1/(2(a+1))]{2cos(a(π/2))}
  = [1/(2(a²-1))]{-4cos(a(π/2))}
  With a = cosθ ωe have
  ∫_-π/2^π/2cos(cosθx)cos(x)dx = 2cos(cosθ(π/2))/(sin²θ).
  
  E_θ(r,t) = [I₀/(2πε₀cr)]cos(ωt - kr)cos[(π/2)cosθ)]/sinθ.
  B_f(r,t) = [μ₀I₀/(2πr)]cos(ωt - kr)cos[(π/2)cosθ)]/sinθ.
  S = (1/μ₀)E×B = (r/r)[I₀²/(4π²ε₀cr²)]cos²(ωt  -kr)cos²[(π/2)cosθ)]/sin²θ.
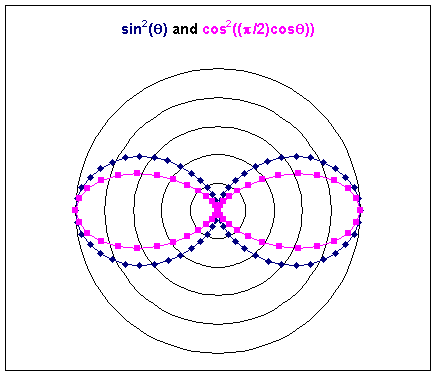
  The plot below compares the angular radiation pattern of a dipole (sin²θ) and a half-wave antenna (cos²[(π/2)cosθ)]/sin²θ).

  

Problem:

A very thin, straight, conducting wire is centered on the origin of coordinates and is oriented along the z-axis.  The wire carries a current I = I₀cos(ω₀t) everywhere along its length l.
(a)  Obtain the vector potential everywhere outside the source region for distances r >> l.  Hint: Use the Lorentz gauge.  Make no assumption about the value of the wavelength, λ₀ = 2πc/ω₀.
(b)  Obtain the dependence of the intensity of the radiation pattern emitted by the wire on the angle θ in the regime  r >> l >> λ₀.

Solution:

• Concepts:
  Potentials in the Lorentz gauge
• Reasoning:
  In the Lorentz gauge the expressions for the potentials are
  Φ(r, t) = [1/(4πε₀)]∫_v' dV' ρ(r', t_r)/|r - r'|,
  A(r,t) = [μ₀/(4π)]∫_v' dV' j(r', t_r)/|r - r'|.
  t_r = t - |r - r'|/c.
• Details of the calculation:
  (a)  Let r >> l.  Then |r - r'| ≈ r[1 - r∙r'/r],
  1/|r - r'| ≈ (1/r)[1 + r∙r'/r].
  Let  j(r', t) = j(r')exp(-iω₀t), then A(r,t) = A(r)exp(-iω₀t), with
  A(r) = [μ₀/(4π)]∫_v' dV' j(r')exp(ik|r - r'|)/|r - r'| with k = ω₀/c.
  Let j = I₀δ(x)δ(y) k for -l/2 < z < l/2,  j = 0 elsewhere.
  Then A(r) = k  [I₀μ₀/(4π)](e^ikr/r)∫_-l/2^l/2 dz'exp(-ik r∙r'/r).
  (In the denominator keep only the zeroth order term and in the exponent keep terms to first order.)
  A(r) = k [I₀μ₀/(4π)](e^ikr/r)∫_-l/2^l/2 dz'exp(-ikz' cosθ)
  = k [I₀μ₀/(4π)](e^ikr/r)[2/(k cosθ)]sin(k(l/2) cosθ)
  = k [1/(4πε₀)][1/(cω₀ cosθ)](2I₀/r)sin(k(l/2) cosθ)e^ikr.
  
  (b)  For r >> l >> λ₀ we have only a radiation fields, proportional to 1/r.
  Then B = ∇×A = (1/r)[∂(rA_θ)/∂r - ∂A_r/∂θ](φ/φ)
  ≈ (1/r)[∂(rA_θ)/∂r](φ/φ) ∝ [sinθ/cosθ]sin(k(l/2) cosθ).
  The power per unit solid angle is proportional to |B²|.
  dP/dΩ ∝ tan²θ sin²(k(l/2) cosθ).
  

  k(l/2) = 2

  
  

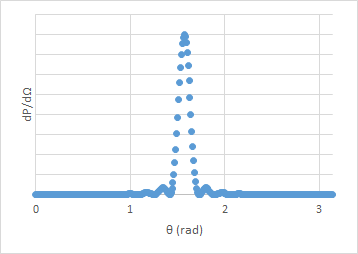
  k(l/2) = 20

  As the ratio  l/λ₀  increases, more and more power is emitted perpendicular to the wire.