Lorentz transformation of the 4-vector current and potential

Problem:

(a)  State Maxwell's equations in differential form.
(b)  State Maxwell's equations in integral form.
(c)  Carry out the Lorentz transformation for the vector potential

A^μ = (-Ex²/c, -(B/2)x², (B/2)x¹, 0)

along the x¹ direction with v = cβ = E/B, (x⁰, x¹, x², x³) are the usual coordinates.  Note E and B are constants and B ≠ 0.  Find the electric and magnetic fields before and after the Lorentz transformation.

Solution:

• Concepts:
  Lorentz transformation of the 4-vector potential,
  E = -∇Φ - ∂A/∂t, B = ∇×A (SI units)
• Reasoning:
  We are asked to Lorentz transform a given 4-vector potential, and from the transformed potential find the transformed fields.
• Details of the calculation:
  (a)  Maxwell's equations in differential form are:
   

  (SI units)

  ∇∙E = ρ/ε0,  ∇×E = -∂B/∂t

  ∇∙B = 0,  ∇×B = μ0j + (1/c2)∂E/∂t

  (b)  Maxwell's equations in integral form in SI units are:

  (1)	∮A E∙dA = Qinside/ε0
  (2)	∮Γ E∙ds = -∂ΦB /∂t
  (3)	∮A B∙dA = 0
  (4)	∮Γ B∙ds =  μ0Ithrough Γ + (1/c2)∂ΦE /∂t

  Φ_B = ∫B∙dA is the flux of B through the area enclosed by the curve Γ.
  Φ_E = ∫E∙dA is the flux of E through the area enclosed by the curve Γ.

  (c) A^μ = (Φ/c, A_x, A_y, A_z) = (-Ey/c, -By/2, Bx/2, 0)
  E = -∇Φ - ∂A/∂t = Ej
  B = ∇ × A = Bk

  These are crossed electric and magnetic fields, they act as a velocity filter.  A charged particle moving with velocity v = iE/B through these fields will experience no force.  The Lorentz transformation must therefore produce a vector potential that yields E' = 0 in the rest frame of that particle.
  Lorentz transformation of the 4-vector potential:
  
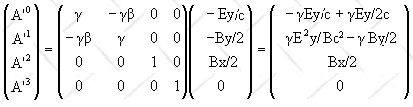
  Here γ = (1 - β²)^-½ ,  β = (E/B)i.
  The coordinates transform as
  
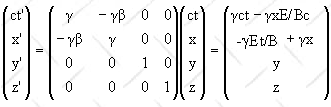
  or
  .
  We therefore have after the Lorentz transformation:
  A'^μ  = (Φ'/c, A'_x, A'_y, A'_z) = (-γEy'/2c, γE²y'/Bc² - γBy'/2, γEt'/2 + γBx'/2, 0)
  E' = -∇'Φ' - ∂A'/∂t' = (γE/2 - γE/2)j = 0
  B' = ∇ × A' = k(γB/2 - γE²/B + γB/2) = k(-γE²/Bc² + γB)

Problem:

A point magnetic moment m is at rest in frame K' and in that frame produces a vector potential A' = (μ₀/4π)m' x r'/r'³ (SI units) and no scalar potential (Φ = 0).  Frame K' moves with constant velocity v << c along the x-axis of frame K, so that an observer in K sees the moment moving with velocity v = βci.  Show that to first order in β the observer in K detects an electric dipole moment p = β x m/c  as well as an undiminished (to first order) magnetic moment m.

Solution: needs work

• Concepts:
  Lorentz transformation of 4-vector potential A'^μ
• Reasoning:
  We transform the 4-vector potential from K' to K and check if it transforms into a vector potential due to a magnetic dipole m and a scalar potential due to an electric dipole p to first order.
• Details of the calculation:
  In the rest frame K' of the magnetic dipole we have A'^μ = (0,A'_x,A'_y,A'_z).
  The dipole is at rest at the origin in K'.
  K moves with velocity -βci = - vi with respect to K'.
  In K we have
  A^μ = (γβA'_x, γA'_x, A'_y, A'_z).
  Since v << c we have γ ~ 1.  We therefore write
  A^μ = (βA'_x, A'_x, A'_y, A'_z).
  x^μ = (ct', x' + βct', y', z'),  i.e.  t = t'  x = x' + βct', y = y', z = z'.
  A(r') = A'(r').  A(r) = A'(r - βcti), the observer in K detects an undiminished (to first order) magnetic moment m = m' moving with velocity βci.
  Φ(r') = cβA'_x(r') = v∙A' = (μ₀/4π)v∙(m'×r'/r'³)
  = (μ₀/4π)(r'/r'³)∙(v×m') = (1/(4πε₀))(r'/r'³)∙p,
  with p = v×m'/c² = v×m/c² =  β x m/c.
  Φ(r) =  (1/(4πε₀))((r - βcti)/|r - βcti|³)∙p.
  Φ(r) is the scalar potential of a dipole p moving with velocity βci.

Problem:

In reference frame K a long, straight, neutral wire with a circular cross sectional area A = πr² lies centered on the z-axis and carries a current with uniform current density jk.

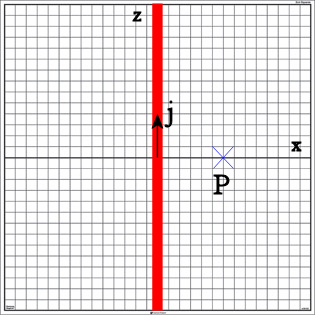
(a)  Find the Φ, A, E, and B at a point P on the x-axis a distance x > r from the wire.
(b)  In a frame K' moving with velocity vk with respect to K, find the ρ, j, Φ, A, E, and B at the point P.
(c)  In a frame K'' moving with velocity vi with respect to K, find the ρ, j, Φ, A, E, and B at the point P.

Solution:

• Concepts:
  Lorentz transformation of 4-vector current, 4-vector potential and electric and magnetic field
• Reasoning:
  We are asked to find ρ, j Φ, A, E, and B in 3 different reference frames.
• Details of the calculation:
  (a) In K we have j = jk inside the wire, j = 0 outside the wire,  ρ = 0 everywhere.
  Outside a neutral wire carrying a current I = jA in the z-direction we have
  E = 0, Φ = 0, B = μ₀I/(2πr)(r/r), A = -[μ₀I/(2π)] ln(r/r₀) k.
  Here r is a cylindrical coordinate.
  At point P on the x-axis B = μ₀I/(2πx) j, A = C - [μ₀I/(2π)] ln(x) k. 
  C is an arbitrary constant.  Chose C = 0.
  (b)  In a frame K' moving with velocity vk with respect to K we have
  cρ' = γcρ - γβj = -γβj.  j_z' = γj inside the wire, ρ' = j' = 0 outside the wire.
  The wire is not neutral in this frame.
  Given ρ' and j' we find Φ' = [γ(v/c²)I/(2πε₀)]ln(x)
  and A' = -[μ₀γI/(2π)]ln(x) k at point P.
  Note x' = x.
  From the potentials we obtain E' = (-i) γ(v/c²)I/(2πε₀x) = (-i) μ₀γvI/(2πεx)
  and B' = μ₀γI/(2πx) j at point P.
  We can also transform the 4-vector potential directly.
  Φ'/c  = - γβA_z = [γβμ₀I/(2π)]ln(x), A_z' = γA_z, A' = -[μ₀γI/(2π])ln(x) k at point P.
  Transforming the fields directly we obtain E_z' = B_z' = E_y' = B_x' = 0,
  B_y' = μ₀γI/(2πx), E_x' = -μ₀γvI/(2πε₀x) at point P.
  All the transformations yield consistent results.
  (c)  In a frame K'' moving with velocity vi with respect to K we have
  ρ' = 0, j_z' = j inside the wire, ρ' = j' = 0 outside the wire.
  The wire is neutral in this frame.
  Transforming the 4-vector potential we find Φ' = 0,
  A' = -[μ₀I/(2π)]ln(γ(x' + vt')) k at point P.
  At point P we have B' = B_y'j, B_y' =  -∂A_z'/∂x' = μ₀γI/(2π(γ(x' + vt')),
  E' = -∂A'/∂t' = μ₀γvI/(2πε₀γ(x' + vt')) k.
  Transforming the fields directly we obtain
  E_x' = B_x' = 0, B_y' = μ₀γI/(2πγ(x' + vt')), E_z' = μ₀γvI/(2πε₀γ(x' + vt')) at point P.
  Even thought we have no charge density, we have an electric field.  Why?

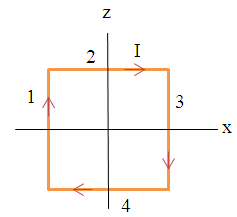
Problem:

In reference frame K a wire with a circular cross sectional area A = πr² forms a square of side length L.  The square lies in the xz-plane.  A current with uniform current density j flows clockwise through the wire, I = jπr².

(a)  In a frame K' moving with velocity vi with respect to K, find the charge density ρ' and the current density j'.
(b)  Find the current flowing in the wire in K'.

Solution:

• Concepts:
  Lorentz transformation of 4-vector current
• Reasoning:
  (cρ, j) is a 4-vector.
• Details of the calculation:
  In K we have j = jk inside the wire for side 1, j = -jk inside the wire for side 3, j = ji inside the wire for side 2, j = -ji inside the wire for side 4, j = 0 outside the wire, ρ = 0 everywhere.
  In a frame K' moving with velocity  vi with respect to K we have j = 0, ρ = 0 outside the wire.
  for side 1:  cρ' = γcρ = 0. j_z' = j_z = j at a position inside the wire
  for side 3:  cρ' = γcρ = 0. j_z' = j_z = -j at a position inside the wire.
  Wires 1 and 3 are neutral in K'.
  for side 2: cρ' = γcρ - γβj_x = -γβj,  j_x' = γj_x = γj at a position inside the wire,
  for side 4: cρ' = γcρ - γβj_x = γβj,  j_x' = γj_x = -γj at a position inside the wire,
  Wires 2 and 4 is not neutral in this frame.
  (b)  The cross sectional area of wires 1 and 3 is an ellipse of area πr²/γ.  The current flowing in those wires in frame K' is I' = jπr²/γ = I/γ.  The same current must flow in all wires.
  The cross sectional area of wires 2 and 4 in K' is πr², the same as in K,  But the current density at a point that at a time t' lies inside the moving wire is due to both the current in the wire and the moving charged wire. 
  Consider side 2:  γj = -ρ'v + j'' = γβ²j + j'', where j'' is the current density due to the current flowing in the wire.
  j'' = γj(1 - β²) = j/γ.  I'' = j''πr² = I/γ.

Problem:

Consider a point charge q at rest at the origin in reference frame K.  Reference frame K' moves with velocity v = cβi with respect to K.  At t = 0 the origins of the two frames coincide.
(a)  Write down expressions for the 4-vector potential A^μ and the 4-vector current j^μ in reference frame K.
(b)  Find A'^μ and j'^μ in reference frame K'.

Solution:

• Concepts:
  Lorentz transformation of the 4-vector potential and 4-vector current
• Reasoning:
  We are asked to find and Lorentz transform the 4-vector potential and 4-vector current.
• Details of the calculation:
  (a)  A^μ = (Φ/c, A_x, A_y, A_z) = (Φ/c, A), j^μ = (cρ, j_x, j_y, j_z) = (cρ, j).
  In K we have j = 0 and we choose the gauge so A = 0.
  ρ(r,t)  = qδ(r),
  Φ(r,t) =  kq/r, with k = 1/(4πε₀).
  A^μ(r,t) = (kq/((x² + y² + z²)^½c), 0, 0, 0),
  j^μ(r,t) = (cqδ(xi + yj + zk), 0 0, 0) = (cqδ(x) δ(y) δ(z), 0 0, 0).
  Both A^μ and j^μ only have a non-zero zero component.

  (b)  Lorentz transformation of the 4-vectors:
  j'⁰(r,t) = γcρ(r,t),   j'¹(r,t) = -γβcρ(r,t).
  A'⁰(r) = γΦ(r)/c,   A'¹(r) = -γβΦ(r)/c.
  But we would like to know  j'^μ(r',t') and A'^μ(r',t').
  We also have to transform the coordinates.
  x = γβct' + γx', y = y', z = z'.
  A'^μ(r',t') = (γkq/[((γβct' + γx')² + y'² + z'²)^½c], -γβkq/[((γβct' + γx')² + y'² + z'²)^½c], 0, 0),
  j'^μ(r',t') = (γcqδ(γ(βct' + x')) δ(y) δ(y), -γβcqδ(γ(βct' + x')) δ(y) δ(y), 0, 0)
  = (cqδ(βct' + x') δ(y) δ(y), -βcqδ(βct' + x') δ(y) δ(y), 0, 0),
  since δ(ax) = δ(x)/|a|.
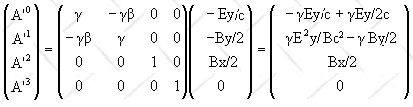
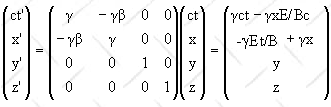