Lorentz transformation of the electromagnetic fields

Problem:

A long superconducting solenoid with radius R is at rest in frame K.  It has its axis along the z-axis and a current flowing on the surface produces a uniform field inside.
(B = Bk, r < R; B = 0, r > R.)

An observer moves with uniform velocity v = vi (v << c) along the x-axis.  Write down the electric and magnetic fields in the rest frame K' of the observer for r < R and r > R.

Solution:

• Concepts:
  Lorentz transformation of electric and magnetic fields
• Reasoning:
  We are asked to transform the electromagnetic fields from the laboratory frame K to a frame moving with uniform velocity v = vi with respect to K.
• Details of the calculation:
  In the laboratory frame K we have E = 0, B = Bk, r < R; B = 0, r > R.
  In K' we observe E'_|| = E_||,  B'_|| = B_||,  E'_⊥ = γ(E + v×B)_⊥,  B'_⊥ = γ(B - (v/c²)×E)_⊥.
  Since v << c we have γ ~ 1.
  Therefore E'_|| = 0,  B'_|| = 0,  E'_⊥ = v×B,  B'_⊥ = B.
  E' = -vBj,  B' = Bk, r < R; E' = 0, B' = 0, r > R.

Problem:

A neutral conducting sphere is at rest with its center at the origin in reference frame K.  A uniform magnetic field B = B₀k is present.  Reference frame K' moves with uniform velocity v = vi with respect to K.  Find E an B inside the sphere as observed in K'.

Solution:

• Concepts:
  Lorentz transformation of the electromagnetic fields
• Reasoning:
  We are asked to transform the electromagnetic fields from the laboratory frame K to a frame moving with uniform velocity v = vi with respect to K.
• Details of the calculation:
  In SI units the transformation of the electromagnetic fields from the laboratory frame to a frame moving with velocity v with respect to the laboratory frame is given by:
  E'_|| = E_||,  B'_|| = B_||,  E'_⊥ = γ(E + v×B)_⊥,  B'_⊥ = γ(B - (v/c²)×E)_⊥.
  In K we have E = 0, B = B₀k.
  In K' we have E_x = 0,  B_x = 0, E'_⊥ = γv×B = -vγB₀j,  B'_⊥ = γB = γB₀k.
  Is there a force on the electrons on the conductor?
  F' = -q_e(E' + v'×B'), where v' = -vi and q_e = 1.6*10^-19 C.
  F' = -q_e(-vγB₀j - (vi)×(γB₀k)) = 0.
  The total force on the electrons inside the conductor is zero.

Problem:

The infinite xy plane is a non-conducting surface with surface charge density σ, as measured by an observer at rest on the surface.  A second observer moves with velocity vi in the positive x-direction with respect to the surface at height h above it.  Find an expression for the electric field and magnetic field measured by this observer.

Solution:

• Concepts:
  Lorentz transformation of the electromagnetic fields
• Reasoning:
  The observer at rest with respect to the surface sees only an electric field.  The magnetic field is zero.  We can transform those field to a frame moving with velocity vi.
• Details of the calculation:
  Let K be the frame of the observer at rest on the surface and K' the frame of the observer moving relative to the surface.
  In K E = σ/(2ε₀)k  for positive z and E = -σ/(2ε₀)k  for negative z (from Gauss' law).
  E = E_⊥.  B = 0.
  In K' we have E'_⊥ = γ(E + v×B)_⊥ = γE_⊥.  B'_⊥ = γ(B - (v/c²)×E)_⊥ = -γ(v/c²)×E.
  Therefore E' = γσ/(2ε₀)k  = [σ/(2ε₀)]*(1 - v²/c²)^-½ k  for positive z.
  B' = γ(v/c²)σ/(2ε₀)j  = [σ/(2ε₀)]*(v/c²)(1 - v²/c²)^-½ j  for positive z.

Problem:

A proton of mass m₀ moving with speed β_z in the z-direction, encounters a quadrupole magnetic field of the form B = B₀xj + B₀yi over a length L along the z-direction.  Both the magnetic field B and the length L are as observed in the laboratory frame.
(a)   Find the electric field experienced by the particle as a function of x and y in its rest frame.
(b)   If the magnet is short enough, such that the acceleration of the particle going through the field can be considered an impulse, (i.e. the acceleration changes the direction, but not the position), find the impulse observed in the lab and the entering particle's rest frame, for a particle that enters the magnet at x = x₀, y = 0.  Explain the difference.

Solution:

• Concepts:
  Lorentz transformation of the electromagnetic fields
• Reasoning:
  We are asked to transform the electromagnetic fields from the laboratory frame to the rest frame of the proton.
• Details of the calculation:
  (a)  In SI units he transformation of the electromagnetic fields from the laboratory frame to a frame moving with velocity v with respect to the laboratory frame is given by:
  E'_|| = E_||,  B'_|| = B_||,  E'_⊥ = γ(E + v×B)_⊥,  B'_⊥ = γ(B - (v/c²)×E)_⊥.
  In the laboratory frame we have B = B₀xj + B₀yi.
  With v = vk we have v × B = -vB₀xi + vB₀yj.
  In a frame moving with velocity vk (i.e. in the original rest frame of the proton) we have:
  E'_z = 0,  B'_z = 0,  E'_x = -γvB₀x',  B'_x = γB₀y',  E'_y = γvB₀y',   B'_y = γB₀x'
  (We have used x = x', y = y'.)
  (b)  In the lab frame the force on the proton is F = qv × B = -qvB₀xi + qvB₀yj .
  This force acts for a short time Δt = L/v. 
  For a proton entering at x = x₀, y = 0 the impulse is I = Δp = -qLB₀x₀i.
  In its original rest frame the force on the proton at x' = x₀, y' = 0 is F = qE = -γqvB₀x₀i. 
  This force acts for a short time Δt = L'/v, the time it takes the magnet to move over the initial position of the proton.  The impulse is I' = Δp' = -γqL'B₀x₀i.
  The momentum is a 4-vector.  The components perpendicular to the relative velocity are the same in two frames moving with respect to each other.  We need Δp = Δp', L' = L/γ, we need the Lorentz contraction.

Problem:

Plot E and B as a function of time at a point P one cm away from the path of a 10 MeV proton.  Set P at (0, 0.01, 0) with the charge at (-vt, 0, 0).

Solution:

• Concepts:
  The electromagnetic fields of a moving point charge, the Lorentz transformation of the electromagnetic fields
• Reasoning:
  In the rest frame of the proton the electric field is the Coulomb field and the magnetic field is zero.  We can transform those field to a frame in which the proton is moving with velocity -vi.
• Details of the calculation:
  Let K be the rest frame of the proton.  In K,  E = (q_e/(4πε₀r²))(r/r),  B = 0.
  Let K' be the frame in which the proton is moving with velocity -vi.  K' is moving with velocity vi with respect to K.
  In SI units the transformation of the electromagnetic fields to a frame K' moving with velocity v with respect to the frame K is given by:
  E'_|| = E_||,  B'_|| = B_||,  E'_⊥ = γ(E + v×B)_⊥,  B'_⊥ = γ(B - (v/c²)×E)_⊥.
  Therefore
  E'_x = E_x = (q_e/(4πε₀))(x/(x² + y² + z²)^3/2
  = (γq_e/(4πε₀))(x' + vt')/(γ²(x' + vt')² + y'² + z'²)^3/2,
  E'_⊥ = γE_⊥, E'_y = (γq_e/(4πε₀))y'/(γ²(x' + vt')² + y'² + z'²)^3/2,  
  E'_z = (γq_e/(4πε₀))z'/(γ²(x' + vt')² + y'² + z'²)^3/2.
  
  B'_x = 0,  B'_⊥ = -γ(vi/c²)×E,  B'_y = γ(v/c²)E_z = (v/c²)E'_z,  B'_z = -γ(v/c²)E_y = -(v/c²)E'_y.
  In K' at x' = 0, y' = y₀' = 0.01, z' = 0 we have
  E'_x = (γq_e/(4πε₀))vt'/(γ²(vt')² + y₀'²)^3/2, E'_y = (γq_e/(4πε₀))y₀'/(γ²(vt')² + y₀'²)^3/2,  E'_z = 0.
  B'_x = 0,  B'_y = 0, B'_z = -(v/c²)E'_y.

  10 MeV proton:  γmc² = (938.28 + 10)MeV,  γ = 1.01,  β = 0.145, v = 4.35*10⁷ m/s.
  E'_x = 1.01*9*10⁹*1.6*10^-19*4.35*10⁷ t(s)/[(1.01*4.35*10⁷)²t² + 10^-4]N/C
  = 6.3*10^-2t/(1.9*10¹⁵t² + 10^-4)N/C.
  E'_y = -1.01*9*10⁹*1.6*10^-19*10^-4/[(1.01*4.35*10⁷)²t² + 10^-4]N/C
  = 1.5*10^-11/(1.9*10¹⁵t² + 10^-4)N/C.

  

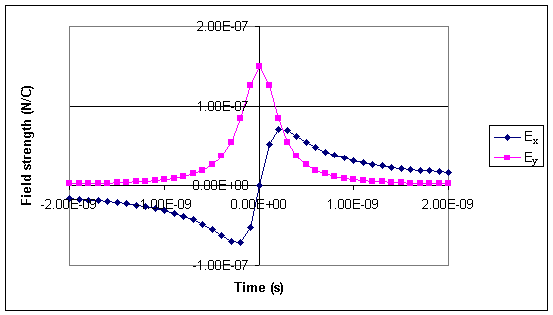
  Here γ = 1.01 is nearly equal to 1.  The electric field in K' differs very little from the instantaneous Coulomb field.  But using the transformation of the fields we can calculate the magnetic field in K'.

Problem:

A 30 GeV proton passes 10^-7cm away from a hydrogen atom.
(a)  Estimate the peak magnitude of the electric field and the duration of the electric field pulse to which the atom is subjected.
(b)  Do the same for a 30 GeV electron passing at the same distance.
You may use m_pc² = 1 GeV and m_ec² = 0.5 MeV.

Solution:

• Concepts:
  The electromagnetic fields of a moving point charge, the Lorentz transformation of the electromagnetic fields
• Reasoning:
  In the rest frame of the proton the electric field is the Coulomb field and the magnetic field is zero.  We can transform those field to a frame in which the proton is moving with velocity vi.
• Details of the calculation:
  (a)  γmc² = 30 GeV, γ ~ 30,  v ~ c.
  The electric field in the proton frame is the Coulomb field, E = kq_e/r²(r/r).
  In the frame of the hydrogen atom we have E'_|| = E_||,  E'_⊥ = γE_⊥.
  In the proton frame the maximum field the hydrogen atom is subjected to is E_max = E_⊥-max = kq_e/b².
  Therefore in the frame of the hydrogen atom E'_max = E'_⊥-max = γkq_e/b².
  E'_⊥-max = [30*9*10⁹*1.6*10^-19/10^-18](N/C) = 4.3*10¹⁰ N/C.
  To estimate the duration of the electric field pulse we can, for example, estimate the time interval during which E > E_max/2.
  In the proton frame E = kq_e/(b² + (vt)²), so when vt = b the E = E_max/2.
  Δt = 2b/v is the duration of the pulse in the proton frame.
  The duration of the pulse in the frame of the hydrogen atom is a proper time interval.
  Δt' = Δt = 2b/(γv).  Δt' = 2*10^-9/(30 c) = 2.22*10^-19 s
  For a 30 GeV electron γ ~ 6*10⁴.
  E_max = 8.6*10¹³ N/C,  Δt' =  1.1*10^-22 s

Problem:

A fixed dipole moment is pointing in the x-direction while moving in the z-direction with a constant velocity v << c.  What are the instantaneous electric and magnetic fields at a point (x, y = 0, z) away from the dipole?

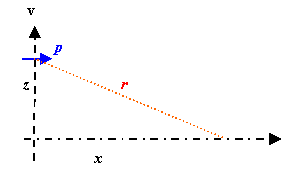
Solution:

• Concepts:
  The electric field of a charge distribution moving with constant velocity v and v << c is the instantaneous Coulomb field.  Here it is the instantaneous dipole field.
  B(r,t) = (v/c²)×E(r,t),  (SI units)
• Reasoning:
  We have a dipole moving with constant velocity and v << c.
• Details of the calculation:
  E(r,t) = (1/(4πε₀)) (1/r'³)[3(p∙r')r'/r'² - p],
  r' = r - R, R = location of the dipole at time t.
  p = pi,  R = (z₀ + vt)k,  r = xi + zk,  r' = r - R =  xi + (z - z₀ - vt)k.
  Let z₀ = 0.
  E(r,t) = (1/(4πε₀))(x² + (z - vt)²)^-3/2[3px(xi + (z - vt)k)/(x² + (z - vt)²) - pi]
  = (1/(4πε₀))(x² + (z - vt)²)^-5/2[2px²i - p(z - vt)²i + 3px(z - vt)k]
  B(r,t) = (v/c²)×E(r,t) = (v/c²)k×E(r,t)
  =  (v/(4πε₀c²))(x² + (z - vt)²)^-5/2[2px²j - p(z - vt)²j]

Problem:

A line of charge with charge density λ C/m is fixed at rest along the x' axis of a reference frame S'.  A test charge q is at rest in S' at (0, 0, z' = d).  S' is in constant motion with velocity v = vi with respect to a reference frame S.
(a)  Calculate the electric field of the line of charge in the rest frame S' and the force on q. 
(b)  Calculate the electric and magnetic fields of the line of charge measured by an observer at rest in S.
(c)  Calculate the force measured by the observer in S on the test charge q.

Solution:

• Concepts:
  Lorentz transformation of the electromagnetic fields
• Reasoning:
  We are asked to transform the electromagnetic fields from the frame S' to a frame moving with uniform velocity v = -vi with respect to S'.
• Details of the calculation:
  (a)  Let r be the perpendicular distance from the x-axis, r' = r.
  In frame S':  E' = λ/(2πε₀r)(r/r),  F' = qE' = kqλ/(2πε₀d).
  (b) S moves with velocity -vi with respect to S'.
  Transformation of the fields:
  E'_|| = E_||,  B'_|| = B_||,  E'_⊥ = γ(E + v×B)_⊥,  B'_⊥ = γ(B - (v/c²)×E)_⊥.  (SI units)
  Here || and ⊥ refer to the direction of the relative velocity.
  We therefore have in S:  E_|| = B_|| = 0,
  E = γλ/(2πε₀r)(r/r),  B = γvλ/(2c²πε₀r)(φ/φ),  where (φ/φ) is a unit vector encircling the x axis according to the right-hand rule.  At (0, 0, z = d) it points into the -j direction.
  (c)  Force on the test charge in S:
  F = kγqλ/(2πε₀d) - kγqv²λ/(2c²πε₀d) = kγ^-1qλ/(2πε₀d) = γ^-1F'.
  Explain the difference:  F = dp/dt.  The momentum is a 4-vector.  The components perpendicular to the relative velocity are the same in two frames moving with respect to each other.  We have Δp = Δp', dτ = dt' = dt/γ.

Problem:

Use the transformation properties of the electromagnetic fields,
E'_|| = E_||,  B'_|| = B_||,
E'_⊥ = γ(E + v×B)_⊥,
B'_⊥ = γ(B - (v/c²)×E)_⊥.
to show that (E∙B)² and E² - c²B² are invariant under a Lorentz transformation.

Solution:

• Concepts:
  Vector products
• Reasoning:
  We can choose a Cartesian coordinate system and evaluate the products using Cartesian coordinate.
• Details of the calculation:
  Let the direction of the relative velocity of K' with respect to K be the z-direction.
  Then E_|| = E_z k and  E_⊥ = E_y i + E_y j,  B_|| = B_z k and  B_⊥ = B_y i + B_y j, 
  E∙B = E_xB_x + E_yB_y + E_zB_z.
  E'∙B' = E'_||∙B'_|| + E'_⊥∙B'_⊥.  E'_||∙B'_|| = E'_zB'_z = E_zB_z.
  E'_⊥ = E'_y i + E'_y j.  B'_⊥ = B'_y i + B'_y j.
  E'_x= γ(E_x - vB_y),  E'_y= γ(E_y + vB_x),  B'_x= γ(B_x + (v/c²)E_y),  B'_y= γ(B_y - (v/c²)E_x).
  E'_xB'_x = γ²(E_xB_x + (v/c²)E_xE_y - vB_yB_x - (v²/c²)B_yE_y).
  E'_yB'_y = γ²(E_yB_y - (v/c²)E_yE_x + vB_xB_y - (v²/c²)B_xE_x).
  E'_xB'_x + E'_yB'_y = γ²(1 - v²/c²)( E_xB_x + E_y B_y) = E_xB_x + E_y B_y.
  (E∙B)² is invariant under a Lorentz transformation.
  
  Or, in vector notation,
  E'∙B' = E'_||∙B'_|| + E'_⊥∙B'_⊥.  E'_||∙B'_|| = E_||∙B_||
  E'_⊥∙B'_⊥ = γ²(E + v×B)_⊥∙(B - (v/c²)×E)_⊥ = γ²(E_⊥ + v×B_⊥)∙(B_⊥ - (v/c²)×E_⊥)
  = γ²[E_⊥∙B_⊥ - E_⊥∙((v/c²)×E_⊥) + (v×B_⊥)∙B_⊥ - (v×B_⊥)∙ ((v/c²)×E_⊥)]
  = γ²[E_⊥∙B_⊥ - (v×B_⊥)∙ ((v/c²)×E_⊥)]
  since v×E_⊥ is perpendicular to E_⊥ and v×B_⊥ is perpendicular to B_⊥.
  (v×B_⊥)∙((v/c²)×E_⊥) = v²B_⊥∙E_⊥ using (A×B)∙(C×D) = (A∙C) (B∙D) - (A∙D) (B∙C).
  So E'∙B' = E_||∙B_|| + γ²[E_⊥∙B_⊥ - (v²/c²)B_⊥∙E_⊥)] = E∙B.

  E² - c²B² = E_xE_x + E_yE_y + E_zE_z - c²(B_xB_x + B_yB_y + B_zB_z).
  E'_zE'_z - c²B'_zB'_z = E_zE_z - c²B_zB_z.
  E'_xE'_x = γ²(E_x² - 2vE_xB_y + v²B_y²).
  E'_yE'_y = γ²(E_y² + 2vE_yB_x + v²B_x²).
  B'_xB'_x = γ²(B_x² + 2(v/c²)E_yB_x + (v²/c⁴)E_y²).
  B'_yB'_y = γ²(B_y² - 2(v/c²)E_xB_y + (v²/c⁴)E_x²).
  E'_xE'_x + E_y'E'_y - c²(B'_xB'_x + B'_yB'_y)
  = γ²(E_x² + v²B_y² + E_y² + v²B_x² - c²B_x² - (v²/c²)E_y² - c²B_y² - (v²/c²)E_x²)
  = γ²(1 - v²/c²)(E_x² + E_y²) - γ²(c² - v²)(B_x² + B_y²) = E_xE_x + E_yE_y - c²(B_xB_x + B_yB_y).