Newton's 2nd law, drag

Problem:

An object of mass m is launched from a stationary helicopter towards the Earth with the speed v₀.   It experiences a force of air resistance F = -kv, where k is a positive constant.   The positive direction of all vector quantities is downward.
(a)  Draw a free body diagram showing the forces acting on the object.
(b)  What is the terminal speed of the object?
(c)  Find the speed of the object as a function of time, v₀, m, g and k.
(d)  What is the direction of the acceleration of the object?

Solution:

• Concepts:
  Newtonian mechanics
• Reasoning:
  F_net = ma is the equation of motion for the object
• Details of the calculation:
  (a)  Since velocity is downward, air resistance is upward, in the opposite direction of gravity.
  
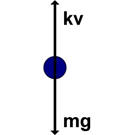
  (b) When the object reaches terminal velocity, its acceleration is a = 0 and the sum of all forces acting on the object is 0.
  0 = mg - kv_t,  v_t = mg/k.
  (c) a = dv/dt
  m(dv/dt) = mg - kv,  dv/(v - mg/k) = -(k/m)dt
  ∫ dv/(v - mg/k)  = -∫(k/m)dt
  ln(v - mg/k) - ln(v₀ - mg/k) = -(k/m)t
  v = mg/k + (v₀ - mg/k)e^-(k/m)t
  (d) a = dv/dt
  a = (-k/m)(v₀ - mg/k)e^-(k/m)t
  a = (g - v₀k/m)e^-(k/m)t
  The acceleration can be positive, negative or zero.
  If v₀ < v_t = mg/k, the acceleration is positive or downward
  If v₀ > v_t = mg/k, the acceleration is negative or upward.
  If v₀ = v_t = mg/k, the acceleration is zero.

Problem:

A particle of mass m falls subject to the pull of gravity, with acceleration g, and to the force of air resistance.  The particle is dropped from height z = z₀.  The initial velocity is zero.  The force of air resistance may be modeled as linearly dependent on the speed, so that the height of the projectile satisfies 

md²z/dt² = -mg - bdz/dt.

(a)  Solve the equation of motion for the particle's height z(t).  Find the terminal velocity.
(b)  Take the b --> 0 limit and show that usual free-fall solution is obtained.

Solution:

• Concepts:
  Newton's second law, integrating the equation of motion
• Reasoning:
  The equation of motion is given. 
• Details of the calculation:
  (a)  Let v = dz/dt, then mdv/dt = -mg - bv.  Try a solution v = A + Be^-kt.
  v(t) = -(g/k) + (g/k)e^-kt, where k = b/m.
  As t approaches infinity, v approaches v_termial = -g/k.
  z(t) = z₀ + ∫₀^t(-(g/k) + (g/k)e^-kt')dt' = z₀  - (g/k)t + (g/k²)(1 - e^-kt).
  (b)  As b --> 0, k --> 0, e^-kt = 1 - kt + k²t²/2 +... .
  z(t) = z₀  - (g/k)t + (g/k²)( kt - k²t²/2) = z₀ - gt²/2.

Problem:

The forces acting on a sky-diver of mass m are the force of gravity and the drag force due to the air.  Assume the drag force is proportional to the square of the speed.  Find the diver's velocity as a function of time, and the diver's terminal velocity v_f.  Assume v_i = 0.

Hint:  ∫dx/(a² - x'²) = (1/a) tanh^-1(x/a)

Solution:

• Concepts:
  Newton's second law
• Reasoning:
  Let the diver's mass be m and the coefficient of proportionality between the drag force and v² be mk.
  mdv/dt = mg - mkv².
• Details of the calculation:
  Terminal velocity v_f = V:  dv/dt = 0  --> V² = g/k.
  In terms of V, dv/dt = g(1 - v²/V²),    dv/(V² - v²) = (g/V²)dt.
  ∫₀^vdv'/(V² - v'²) = gt/V².
  Integrating and solving for v we get
  v(t) = V tanh(gt/V).  

Problem:

A boat with mass m is slowed by a drag force F(v).  Its velocity decreases according to the formula v(t) = c²(t - t_f)² for t ≤ t_f, where c is a constant and t_f is the time a which it stops.  Find the force F(v) as function of v.

Solution:

• Concepts:
  Newton's second law
• Reasoning:
  F = mdv/dt.
• Details of the calculation:
  a(t) = dv/dt = 2c²(t - t_f).
  F(t) = ma(t) = 2mc²(t - t_f).
  t - t_f = -√(v)/c  (Select the negative solution since t - t_f is negative.)
  F(v) = -2mc²√(v)/c = -2mc√(v).

Problem:

Assume a particle of mass m is subject to a damping and a driving force.  Its equation of motion is
dv/dt = -λv + (F/m)exp(iωt).
(The physics is represented by the real part of the equation.)
Find the general (real) solution for v(t).

Solution:

• Concepts:
  Solving a differential equation
• Reasoning:
  We find the solution to the inhomogeneous equation dv/dt + λv = (F/m)exp(iωt)
  and add the solution of the homogeneous equation dv/dt + λv = 0.
• Details of the calculation:
  (a)  inhomogeneous solution:
  Try v = A exp(iωt),  iωA + λA = F/m.  A = (F/m)/(iω + λ).
  homogeneous solution:
  v = v₀exp(-λt), v₀ = arbitrary real constant.
  general solution:
  v = v₀exp(-λt) - (F/m)exp(iωt)/(iω + λ).
  Real part: v(t) = v₀exp(-λt) + (Fω/m)sin(ωt)/(ω² + λ²) - (Fλ/m)cos(ωt)/(ω² + λ²).
  v(t) = v₀exp(-λt) + [(F/m)/(ω² + λ²)](ω sin(ωt) - λ cos(ωt)).