Newton's 2nd law, friction

Problem:

A box of mass m slides across a horizontal table with coefficient of friction μ.  The box is connected by a rope which passes over a frictionless pulley to a body of mass M hanging along side the table.  Find the acceleration of the system and the tension in the rope.

Solution:

• Concepts:
  Newton's second law
• Reasoning:
  For each box we have F = ma.  The magnitude of a is the same for each box.
• Details of the calculation:
  
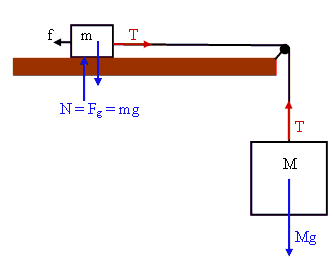
  Mg - T = Ma.
  T - f = ma.
  f = μmg.
  a = (M - μm)g/(M + m),  T = Mg - Ma = Mmg(1 + μ)/(m + M).

Problem:

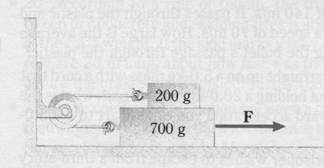
In the figure below the coefficient of friction is the same at the top and the bottom of the 700-g block. 
(a)  Draw a free body diagrams for both the 200-g and the 700-g blocks, considering all forces.
(b)  If the acceleration is a = 70 cm/s² when F = 1.3 N, how large is the coefficient of friction?

Solution:

• Concepts:
  Newton's second law
• Reasoning:
  This is a simple Newtonian Mechanics problem.
• Details of the calculation:
  (a)  Forces acting in the horizontal direction:
  
  (b) F - T - f₁ - f₂ = Ma,  T - f₂ = ma.
  f₁ = μ(M + m)g,  f₂ = μmg.
  F - ma - f₁ - 2f₂ = Ma.
  F - μ Mg - 3μ mg = (M + m)a.
  μ = [F - (M + m)a]/[Mg + 3mg].
  μ = [1.3 - 0.9*0.7]/[1.3*9.8] = 0.0526 .

Problem:

A trunk weighing 500 N is to be pushed up a rough incline by an applied horizontal force F.  The incline makes an angle of 40^o with the horizontal.  If a force of 1000 N is sufficient to move the trunk at a constant velocity of 0.200 m/s, what is the coefficient of kinetic friction between the trunk and the incline?

Solution:

• Concepts:
  Newton's 2^nd law, the force of friction, the normal force, the gravitational force
• Reasoning:
  The trunk is moving in an inertial frame with constant velocity.  It is not accelerating, Newton's 2^nd law requires that the net force is zero.  In addition to the applied force, the force of friction, the normal force, and the gravitational force are acting on the trunk
  The vector sum of all the forces acting on the trunk must be zero.
• Details of the calculation:
  
  Choose the axes of your coordinate system as shown.  The x- and y-components of the net force must be zero.
  x-component: 
  f + mg sin(40^o) - F_acos(40^o) = 0.  Solve for f. 
  f = (1000 N) cos(40^o) - (500 N) sin(40^o) = (444.65 N).
  y-component: 
  N - mg cos(40^o) - F_asin(40^o) = 0.  Solve for N.
  N = mg cos(40^o) + F_asin(40^o) = (1025.81 N).
  Use f = μN to find the coefficient μ.
  μ = f/N = 0.43.

Problem:

A block is given a quick push along a horizontal table.  The coefficient of kinetic friction between the block and the table is μ_k.  It is known that during the time interval t (immediately after the push) the block covers a distance d.  Find the distance that may be covered by the block during the subsequent time interval t'.  Find all possible answers.

Solution:

• Concepts:
  Newton's 2^nd law, friction, kinematics
• Reasoning:
  The force of kinetic friction is responsible for the acceleration of the block.
• Details of the calculation:
  Let the block's mass be m, its momentum just after it received the impulse be p = mv₀i.
  dp_x/dt = -μ_kmg until the block comes to rest.
  Therefore p_x decreases at a steady rate until the block comes to rest, a_x = μ_kg.
  The block comes to rest at time t_rest = v₀/(μ_kg).
  The block can cover a maximum distance d_max = v₀t_rest - ½μ_kgt_rest² = ½v₀²/(μ_kg).
  Case (a)  t ≥ t_rest, d = d_max, then the distance covered during the subsequent time interval t' is zero.
  Case (b)  t + t' ≥ t_rest, then the distance covered during the subsequent time interval t' is d_max - d.
  Case (c)  t + t' < t_rest, then the distance covered during the subsequent time interval t' is
  d' = v₀(t + t') - ½ μ_kg(t + t')² - d = v₀t' - ½ μ_kg t'² - μ_kgtt'.

Problem:

You are going to entertain children by pulling a tablecloth out from under the the cake at a birthday party.  The birthday cake is resting on a tablecloth at the center of a square table.  Each side of the table has length l =  1.84 m.  The tablecloth is the same size as the table top.  You grab the edge of the tablecloth and pull sharply in a direction along one of the sides.  The tablecloth and cake are in contact for time t after you start pulling.  Then the sliding cake is stopped (you hope) by the friction between the cake and table top.  The coefficient of kinetic friction between the cake and tablecloth is μ_k1 = 0.310 , and that between the cake and table top is μ_k2 = 0.410.  Calculate the maximum value of t if the cake is not to end up on the floor.  Neglect the size of the cake compared to the size of the table.

Solution:

• Concepts:
  Newton's 2^nd laws, kinematics
• Reasoning:
  Let the direction of motion of the tablecloth be the positive x-direction.
  Assume that the cake moves a distance d while still on the tablecloth and a distance Δx while sliding on the table top.
  Assume it falls off the table when its center reaches the edge of the table, i.e. when d + Δx = l/2.
• Details of the calculation:
  (i)  The cake is still in contact with the tablecloth and is moving in the direction of motion of the tablecloth.
  The only force acting on the cake in the horizontal direction is friction.
  f = ma = μ_k1mg,  a = μ_k1g in the positive x-direction..
  d = ½μ_k1gt² is distance the cake slides during its contact with the tablecloth.
  Its velocity when it looses contact with the tablecloth is μ_k1gt, in the positive x-direction.
  (ii)  The cake is now in contact with the table.
  Again, the only force acting on the cake in the horizontal direction is friction.
  f = ma = -μ_k2mg,  a = -μ_k2g.  The direction of the acceleration is now in the negative x-direction.
  The cake will move a distance Δx before it comes to rest.
  v_xf² = v_xi² + 2aΔx.  Δx = v_xi²/(2μ_k2g) = (μ_k1gt)²/(2μ_k2g).
  To solve for the maximum t we set d + Δx = l/2.
  ½μ_k1gt_max²  + (μ_k1gt_max)²/(2μ_k2g) = l/2.
  t_max² = l/[g(μ_k1 + μ_k1²/μ_k2)] = 0.345 s2.
  t_max = 0.587 s.

Problem:

In a gravity-free environment a particle of mass m is constrained to move on the inside of a circular track of radius R.  The coefficient of kinetic friction between the particle and the tack is μ.  At t = 0 the particle is given an impulse of magnitude p₀. 
(a)  How long does it take the particle to move once around the track?   
(b)  What is its speed after one revolution?

Solution:

• Concepts:
  Circular motion
• Reasoning:
  For the particle of mass m to move with speed v on the inside of the circular track, the track has to exert a force mv²/R towards the center of the circle.  This is a normal force.
  The frictional force with magnitude f = μN = μ mv²/R will slow the particle down.
• Details of the calculation: (a)  mdv/dt = -μmv²/R,  dv/v² = -(μ/R)dt.
  Integrate:  ∫_v0^v(t)dv'/v'² = -(μ/R)t.  1/v₀ - 1/v(t) = -(μ/R)t.   v(t) = v₀/(1 + (μv₀/R)t).
  The distance s(t) traveled in time t is s(t) = ∫₀^tv(t')dt' = v₀∫₀^tdt'/(1 + (μv₀/R)t').
  s(t) = (R/μ) ∫₁^{1 + (μv0/R)t} dt'/t' = (R/μ)ln(1 + (μv₀/R)t).
  For s(t) = 2πR we have 2πμ = ln(1 + (μv₀/R)t),  exp(2πμ) = 1 + (μv₀/R)t.
  t = (exp(2πμ) - 1)R/(μv₀) = (exp(2πμ) - 1)mR/(μp₀).
  (b)  v_{after one revolution} = v₀/(1 + (exp(2πμ) - 1)) = v₀ exp(-2πμ) = (p₀/m) exp(-2πμ).
  Or
  dv/dt = (dv/ds) ds/dt = ½dv²/ds = - μv²/R.
  v²(s) = v₀²exp(-2μs/R),  v(s) = v₀exp(-μs/R),  v_{after one revolution} = v₀ exp(-2πμ).
  v(s) = ds/dt  dt = ds/v(s)  = ds exp(μs/R)/v₀.
  Integrate from 0 to 2πR to find t(2πR) = (exp(2πμ) - 1)R/(μv₀).