Uniform circular motion, centripetal acceleration

Problem:

The turns at the Daytona Speedway have a radius of 300 m and are banked at about 30^o.
(a)  At what speed does the banked curve provide exactly the centripetal acceleration required to move the car around the curve?
(b)  Ignoring factors other than gravity, what is the maximum speed of the car without sliding, if the coefficient of friction between the road and tires is 0.7?
(c)  What additional forces on the race car allow it to exceed this speed?

Solution:

• Concepts:
  Uniform circular motion,  F_c = mv²/r
• Reasoning:
  F_c = mv²/r.  In part (a) the horizontal component of the normal force must provide all the centripetal acceleration and in part (b) the frictional force must provide part of the centripetal acceleration.
  A free-body diagram of the car on the track is shown below.

  
   

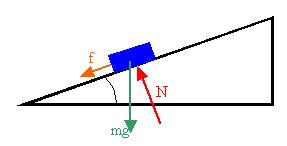
• Details of the calculation:
  Assume the car is traveling with speed v and the frictional force f = 0.  Then
  N cosθ = mg, N sinθ = mv²/r, tanθ = v²/(gr), v² = g*(300 m)*tan(30^o), v = 41.2 m/s.

  (b)  Assume the car is traveling with speed v' and f = f_max.  Then 
  N cosθ - mg - f sinθ  = 0,  N sinθ + f cosθ = mv'²/r.
  With f = 0.7*N we have
  N = mg/(cosθ - 0.7 sinθ),  N(sinθ + 0.7 cosθ) = mv'²/r,
  v'² = gr(sinθ + 0.7 cosθ)/(cosθ - 0.7 sinθ), v = 79.39 m/s.
  (c)  aerodynamic forces (downward lift)

Problem:

A highway curve with a radius of 750 m is banked properly for a car traveling 120 km/h.  If a 1590 kg Porsche rounds the curve at 230 km/h,
(a)  how much sideway force must the tires exert against the road if the car does not skid?
(b)  what must be the bank angle for the Porsche to turn if there is no friction force on the tires?

Solution:

• Concepts:
  Uniform circular motion,  F_c = mv²/r
• Reasoning:
  In part (a) the frictional force must provide part of the centripetal acceleration, in part (b) the horizontal component of the normal force must provide all the centripetal acceleration.
• Details of the calculation:
  (a) A free-body diagram of the car on the track is shown below.
  
  When the car is traveling at v = 120 km/h the frictional force f = 0 and 
  Ncosθ = mg, Nsinθ = mv²/r, tanθ = v²/(gr), θ = 8.6^o.
  When the car is traveling at v' = 230 km/h we have 
  Ncosθ - mg - fsinθ  = 0,  Nsinθ + fcosθ = mv'²/r.
  f(tanθsinθ + cosθ) = mv'²/r - mgtanθ.
  f = 6226 N.
  The tires must exert a sideway force of 6226 N.
  For part (b) the horizontal component of the normal force must equal mv'²/r = 8653.4 N.
  The vertical component of the normal force is mg = 1590 kg(9.8 m/s²) = 15582 N.
  tanθ = 8653.4/15582  θ  = 29^o.  The bank angle must be 29^o.

Problem:

An automobile of mass 1870 kg goes around a curve of radius 38.2 m on a flat, dry, road.  If the coefficient of static friction between the tires and roadway is μ = 0.564, what is the maximum speed that the car can have to make the turn successfully?

Solution:

• Concepts:
  Uniform circular motion,  F_c = mv²/r
• Reasoning:
  Friction has to provide the centripetal acceleration.
• Details of the calculation:
  mv²/R = f ,  mv_max²/R = μmg ,  v_max = (μgR)^½ = (0.564*9.8 m/s²*38.2m)^½ = 14.53 m/s.

Problem:

A motorcyclist rides around the inside of a vertical cylinder of radius 50 feet.  If the coefficient of friction is 0.5, calculate the minimum safe speed.
(Give a numerical answer!)

Solution:

• Concepts:
  Uniform circular motion, centripetal acceleration
• Reasoning:
  The normal force provides the centripetal acceleration. The force of friction cancels gravity.
• Details of the calculation:
  N = Mv²/R,  μN = Mg, v = (gR/μ)^½ = ((9.8 m/s² * 15.4 m)/0.5)^½ = 17.28 m/s.

Problem:

A mass is suspended from a fixed point by a light cord of length L.  The mass is set in motion in a horizontal circle of radius R as shown.  Such an arrangement is called a conical pendulum because the moving cord sweeps out the surface of an inverted cone.

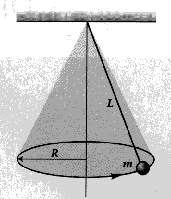
(a)  What is the frequency f of such a conical pendulum in terms of L, R, and g?
(b)  Show that for L much greater than R, the period (T) of a simple pendulum is approximately the same as that of a conical pendulum of the same length.

Solution:

• Concepts:
  Uniform circular motion,  F_c = mv²/r
• Reasoning:
  The mass moves along a circular path with constant speed v.  The centripetal acceleration is v²/R.  The magnitude of the horizontal component of the tension must provide the centripetal force F_c = mv²/R, while the magnitude of the vertical component of the tension must be equal to weight mg.
• Details of the calculation:
  (a)  (mv²/R) /[(mv²/R)² + (mg)²]^½ =  R/L,  v⁴ = R⁴g²/(L² - R²).
  The period of the pendulum is T = 2πR/v = 2π(L² - R²)^¼/g^½.  The frequency is f = 1/T.
  (b)  If L >> R then T ~ 2π(L/g)^½.  This is the period of a simple pendulum of length L.

Problem:

A 20-kg child sits on a turntable at a distance of 1.2 m from the center.  The coefficient of static friction between the child and the turntable is 0.6. 
(a)  If the turntable is rotating at a frequency of 3 revolutions per minute, what is the frictional force exerted by the platform on the child? 
(b)  At what frequency of rotation will the child slide off the platform?

Solution:

• Concepts:
  Uniform circular motion, centripetal acceleration, the frictional force
• Reasoning:
  The frictional force has to provide the centripetal acceleration.
• Details of the calculation:
  (a)  f_s = mv²/r, m = 20 kg, r = 1.2 m, v = 2πr/(20 s).  f_s = 2.37 N.
  (b)  f_s(max) = 0.6*20 kg*9.8 m/s² = 117.6 N, v(max) = (f_s(max)*r/m)^½ = 2.66 m/s.
  frequency: f  = v(max)/(2πr) = 0.352 rad/s = 2.21 revolutions/s.

Problem:

A solid disk of radius R is mounted on a vertical axle.  Initially, the disk is not spinning, and its top surface is covered with dust.  Then the disk begins to spin with a slowly increasing angular speed.  At what value of the angular speed ω would 75% of the disk surface become dust-free?  The coefficient of static friction between the dust particles and the disk surface is μ.

Solution:

• Concepts:
  Circular motion,  F_c = mv²/r
• Reasoning:
  Consider a dust particle a radius r.
  For it to move in a circle, the frictional force f = μmg must provide the centripetal force mrω². 
• Details of the calculation:
  We need ω² = μg/r', for the portion of the disk with radius less or equal to r' to stay dust-covered.
  The area of the disk is πR², so we want πr'² = ¼πR², r' = R/2.
  For ω² = 2μg/R we find that 75% of the disk surface become dust-free.