Conservation laws

Problem:

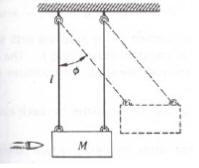
A simple way to measure the speed of a bullet is with a ballistic pendulum.  As illustrated, this consists of a wooden block of mass M into which the bullet is shot horizontally.  The block is suspended from cables of length l, and the impact of the bullet causes it to swing through a maximum angle Φ, as shown.  The initial speed of the bullet is v and its mass is m.
(a)  What is the speed of the block V immediately after the bullet comes to rest inside the wooden block?  (Assume that this happens quickly.)
(b)  Find an expression for the speed v of the bullet in terms of the quantities that can be easily measured m, M, g, l, and Φ.

Solution:

• Concepts:
  Conservation laws
• Reasoning:
  Use conservation of momentum for the first part of the problem and conservation of mechanical energy for the second part.
• Details of the calculation:
  (a)  p_initial = mv,  p_final = (m + M)V,  V = vm/(m + M).
  (b)  Set the zero of the potential energy at zero displacement of the block.
  Just after the bullet comes to rest:  E = T + U = ½(m + M)V² = ½[m²/(m + M)]v².
  When the block reaches the maximum angle Φ:  E = (m + M)gh = (m + M)gl( 1 - cosΦ).
  Energy conservation:  ½[m²/(m + M)]v² = (m + M)gl( 1 - cosΦ),  v² = 2(m + M)²gl( 1 - cosΦ)/m².
  v = [(m + M)/m](2gl(1 - cosΦ))^½.

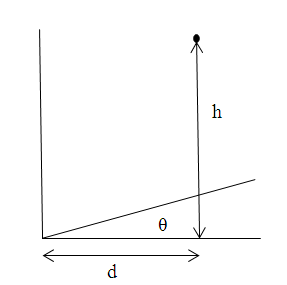
Problem:

An plane, inclined at θ = 20^o, touches a wall as shown in the picture.  You drop a small, perfectly elastic ball from a height h = 1.5 m onto the onto the plane.  The ball falls from rest.  You do not move your hand.  At what distance d from the wall do you have to drop it so that it bounces back into your hand?

Solution:

• Concepts:
  Energy conservation, kinematics
• Reasoning:
  The ball has to retrace its trajectory.  It has to hit the wall at 90^o.
• Details of the calculation:
  When the ball bounces off the plane it makes an angle of 20^o with the normal to the plane or θ' = 50^o with respect to the horizontal.  Assume it has speed v.  Its velocity components are v_x = -vcosθ',  v_y = vsinθ'.  It executes projectile motion and reaches its maximum height at t_{max_height} =  vsinθ'/g.  During this time it travels a distance d = vcosθ'*vsinθ'/g = v²sin(2θ')/(2g).  If the distance to the wall is d, it hits the wall at 90^o and bounces off horizontally.  It then retraces its trajectory.  We need v² = 2gd/sin(2θ'). 
  But ½mv² = mg(h - d tanθ),  (h - d tanθ) = d/sin(2θ'),  d*(1/sin(2θ') + tanθ) = h.
  d = h/(1/sin(2θ') + tanθ) = 1.09 m.

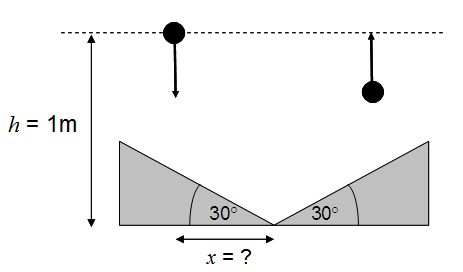
Problem:

Two wedges are placed mirror symmetrically so that the tip of one touches the tip of another as shown in the figure below.  The surface of each wedge is at angle θ = 30 degrees relative to the ground.  A small elastic ball is dropped from height h = 1 m with zero initial velocity.  How far from the tips of the two wedges (x) must the small ball be dropped, so that after bouncing from the two wedges it will reach the same height from where it was dropped?  Neglect any friction from air and consider the bouncing of the ball to be completely elastic.

Solution:

• Concepts:
  Energy conservation, kinematics
• Reasoning:
  The ball's trajectory must be symmetric about the midpoint between the wedges.  It has to cross the midpoint with its velocity having no vertical component. 
• Details of the calculation:
  Just after the ball bounces off the plane its velocity makes an angle of 30^o with the normal to the plane and therefore also an angle of θ' = θ = 30^o with respect to the horizontal.  Assume it has speed v.  Its velocity components are v_x = vcosθ,  v_y = vsinθ.  It executes projectile motion and reaches its maximum height at t_{max_height} =  vsinθ/g.  During this time it travels a distance
  d = vcosθ*vsinθ/g = v²sin(2θ)/(2g).  If the distance to the middle is d, it crosses the midpoint with its velocity having only a horizontal component.  The second half of its trajectory then mirrors the first half.  We need v² = 2gd/sin(2θ). 
  But ½mv² = mg(h - d tanθ),  (h - d tanθ) = d/sin(2θ),  d (1/sin(2θ) + tanθ) = h.
  d = h sin(2θ)/(1 + 2sin²θ) = 0.577 m.

Problem:

A wheel of radius b is rolling along a muddy road with a speed v.  Particles of mud attached to the wheel are being continuously thrown off from all points of the wheel.  If v² > 2bg, where g is the acceleration of gravity, find the maximum height above the road attained by the mud, H = H(b,v,g).

Solution:

• Concepts:
  Energy conservation, projectile motion,
• Reasoning:
  The mud particles are projectiles acted on by the gravitational force.
  Mud particles thrown from different positions on the rim follow different trajectories and rise to different heights.  We will label the position on the rim by some parameter α, calculate the height reached by a particle leaving from this position, and then find the maximum height as a function of the parameter α.
• Details of the calculation:
  
  
  
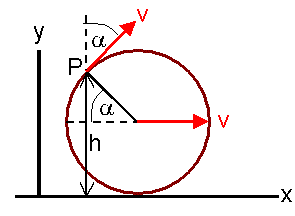
  Assume mud is ejected from a point P, and define α and h as in the figure.  Let Δh be the height the mud rises above the ejection point.  Conservation of energy yields
  mgΔh = (mv_y²)/2 = (mv² cos²α)/2,  Δh = (v² cos²α)/2g.
  The height H reached by the mud is H = h + Δh = b + b sinα + (v² cos²α)/2g.
  We find the maximum height by setting dH/dα = 0. 
  This yields b cosα - (v²/g) cosα sinα = 0.  Two solutions to this equation exist.
  (i)  cosα = 0, α = π/2, H = 2b.
  This is the maximum height only if b sinα + (v² cos²α)/2g ≤ b for all angles α,
  or v² ≤ 2gb.
  Then we do not have v² > 2gb.
  (ii)  sinα = gb/v² = sinα₀.  Then
  H = b + b sinα₀ + v²(1 - sin²α₀)/(2g)
  H = b + gb²/v² + (v²/2g)(1 - g²b²/v⁴)

Problem:

In one dimension, a particle is acted upon by an attractive force F = −kx³.
(a)  Show that the period for the motion of this particle is inversely proportional to the amplitude.
(b)  By contrast show that the period for the motion of a particle subjected to the force F = −kx is independent of the amplitude.

Solution:

• Concepts:
  Energy conservation, periodic motion
• Reasoning:
  The given forces are conservative forces derivable from a potential.  U(x) is a potential well.
• Details of the calculation:
  (a)  The force is a conservative force derivable from a potential.
  U(x) = ¼ kx⁴.
  This is a potential well and the particle's motion will be periodic.
  Energy conservation:  ½m(dx/dt)² +  ¼kx⁴ = E = constant
  Solving for the velocity we obtain dx/dt = (2E/m - kx⁴/(2m))^½.
  Setting dx/dt = 0 we obtain the amplitude of the motion, A = (4E/k)^¼.
  The period is obtained from
  τ = ∫₀^τ dt = 4∫₀^A dx (2E/m  - kx⁴/(2m))^-½ = 4(2m)^½∫₀^A dx (kA⁴  - kx⁴)^-½
  = (4/A)(2m/k)^½∫₀¹ dy (1  - y⁴)^-½,  with x = Ay.
  The period is inversely proportional to the amplitude.
  
  (b)  U = ½kx², we have simple harmonic motion.
  The amplitude for SHM is given by A = (4E/k)^½.  The period is obtained from
  τ = ∫₀^τ dt = 4∫₀^A dx (2E/m  - kx²/(2m))^-½ = 4(2m)^½∫₀^A dx (kA²  - kx⁴)^-½
  = 4(2m/k)^½∫₀¹ dy (1  - y⁴)^-½,  with x = Ay.
  The period is independent of the amplitude.

Problem:

A particle of mass m is subjected to a force whose potential energy is U(x) = ax² - bx³,
with a and b constants and a > 0.
(a)  Find the force.
(b)  Assume that the particle starts at the origin with velocity of magnitude v₀.  Show that if
v₀ < v_C, where v_C is a certain critical velocity, the particle will be confined in a region near the origin.  Find v_C.

Solution:

• Concepts:
  Motion in 1D subject to a conservative force
• Reasoning:
  The potential energy function has a local maximum and a local minimum.  Depending on the total energy of the particle, it can either be trapped in the region of the local minimum, or be free.
• Details of the calculation:
  (a)  F(x) = - dU/dx = -2ax + 3bx².   F = 0 at x = 0 and at x = (2/3)(a/b).
  d²U/dx² = 2a - 6bx.
  At x = 0  d²U/dx² = 2a and at x = (2/3)(a/b)  d²U/dx² = -2a.
  If a > 0 then U(x) has a local minimum at x₁ = 0 and a local maximum at x₂ = (2/3)(a/b).
  There are only two local extrema.  U(x) has an absolute maximum x = -sign(b)*∞ and an  absolute minimum x = sign(b)*∞.

  

  If the particle moves through x = x₁ = 0 with speed v₀ in the direction of -sign(b), its speed will decrease until all its kinetic energy has been converted to potential energy, and then increase again, with the velocity having changed sign.  It will move through the origin with speed v₀ in the direction of sign(b). 
  If the particle moves through x = 0 with speed v₀ in the direction of sign(b), its speed will decrease until all its kinetic energy has been converted to potential energy and then increase again with the particle moving in the opposite direction, unless the particle reached x = x₂ = (2/3)(a/b) with speed v > 0.  It can then move across the potential barrier and it will move with increasing speed in the direction of sign(b).
  The critical speed v_C is found from ½mv_C² = ax₂² - bx₂³ = (4/27)a³/b².
  v_C = (2/(3b))(2a³/m)^½.

Problem:

A ball is dropped down an elevator shaft.  The elevator has an upward speed V.  The instant the ball is dropped, the top of the elevator is below it by a distance h.  How high will the ball rebound above the point from which it was dropped?

Solution:

• Concepts:
  Conservation of mechanical energy, frame transformations
• Reasoning:
  Compared to the ball the elevator is "infinitely" massive. The frame of the elevator is an inertial frame.  In the frame of the elevator, a dropped ball makes an elastic collision with the floor and bounces back.  Its speed just before the collision equals its speed just after the collision.  
• Details of the calculation:
  In the frame of the elevator, the ball has an initial speed V.  It will contact the floor after a time interval Δt.  We have VΔt + ½gΔt² = h, Δt > 0.  The speed of the ball after the time interval Δt is V + gΔt.  In the frame of the elevator the speed of the ball just after the bounce is v = V + gΔt, and the ball is moving upward.
  In the frame of the ground, the speed of the ball just after the bounce is v = 2V + gΔt and the ball is moving upward.  Its kinetic energy is ½mv².  It will rise a distance Δh = ½v²/g above the contact point, which is at  h - VΔt below the point from which the ball was dropped, since in the time interval Δt the elevator as risen a distance VΔt.  In the frame of the ground the ball will therefore rise a distance h' = Δh - h + VΔt above the point from which it was dropped.
  Δt = ((V²+2gh)^½ - V)/g
  v = V + (V²+2gh)^½
  Δh = (V²+gh+V(V²+2gh)^½)/g
  VΔt = (V(V²+2gh)^½ - V²)/g
  h' = (V²+gh+V(V²+2gh)^½)/g + (V(V²+2gh)^½-V²)/g - h = 2V(V²+2gh)^½)/g
  In the frame of the ground, the ball rebounds to a height h' = 2V(V²+2gh)^½)/g above the point from which it was dropped.